JOISC 2024 记录
感觉我太滞后了
Day1 T1 Fish 3
我们可以做的操作是单点加 \(D\) 和后缀加 \(1\)，考虑把这个操作放在差分数组上，则操作变成了：
- 单点加 \(1\)。
- \(i\) 处加 \(D\)，\(i+1\) 处 \(-D\)。
需要最小化第二种操作的使用次数，发现只有对于所有差分数组中的负数是不得不用第二种操作的，而对于其他的，都可以用第 \(1\) 中操作补齐。
\(B_i:=C_i-C_i-1\)，则对于 \(B_i<0\)，我们需要对其进行若干次二操作，使得先变成一个 \(\le B_i\) 的数，然后用一操作补齐。而从它这个地方向前移出去的 \(D\) 都需要有其他的 \(B_i\) 承接。
我们至少需要对其进行 \(\left\lceil\dfrac{-B_i}{D}\right\rceil\) 次而操作，
由此，我们可以将题意转化成：对于 \(B_i<0\) 的位置，我们有 \(\left\lceil\dfrac{-B_i}{D}\right\rceil\) 个右括号；对于 \(B_i\ge 0\) 的位置，我们有 \(\left\lfloor\dfrac{B_i}{D}\right\rfloor\) 个左括号，我们需要进行括号匹配，匹配第 \(i\) 个位置的左括号和第 \(j\) 个位置的右括号的代价是 \(j-i\)，问最小的代价。
通过调整法可知，如果出现匹配 \(i_1,j_1\) 和 \(i_2,j_2\) 有 \(i_1<i_2<j_1<j_2\)，我们将其调整成 \(i_1\) 和 \(j_2\) 匹配，\(i_2\) 和 \(j_1\) 匹配不劣。也就是，我们就是进行贪心的括号匹配。因此，我们在询问一个区间的时候，除了差分数组的第一位，其余的都是原差分数组的子区间，可以发现所有的匹配不会变化。因此，我们初始的时候使用栈模拟匹配，可以得到 \(O(n)\) 对这样的匹配三元组 \((i,j,cnt)\)。
而我们想要查询一个子区间的代价，就是需要知道有那些在这个区域内的左右括号自己匹配了，以及有多少个右括号匹配的左括号不在选择的区间内。
具体的，记 \(v1=\sum\limits_{(i,j,cnt)} [L< i\land j\le R]cnt(j-i),v2=\sum\limits_{(i,j,cnt)} [i\le L<j\le R]cnt,v3=\sum\limits_{(i,j,cnt)} [i\le L<j\le R]cntj\)。
如果 \(C_L\ge D\times v2\)，则有解，最优解为 \(v3-v2\times L+v1\)。
否则，无解。
发现 \(v1,v2,v3\) 都是二维数点，可以使用主席树做到 \(O(n\log n)\)。
Day1 T2 Ski 2
我们先考虑 \(\max H_i\) 是 \(O(N)\) 的怎么做
首先考察几个贪心的结论，我们将所有的地点按照双关键字 \((H_i,C_i)\) 从小到大排序之后，所有 \(C_i\) 的前缀最小值对应的点是不会被移动的，容易通过调整法证明其不优。这也就意味着，我们知道要在某一个高度 \(H\) 上添加一个向前的连边，代价是可以 \(O(1)\) 的得到的。
对于一组确定的解，海拔更高的一层能够容纳的不需要额外修建连接设施的点是非严格递增的，下面给出一张图，可以用于感性理解：
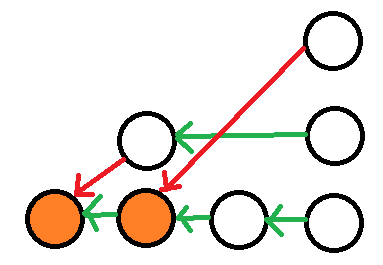
其中橙色点为前缀最小值点，绿色边为原有连接设施连接的边，红色边为额外修建连接设施链接的边。
由此，我们可以设计出 DP 状态 \(f_{i,j,k}\)，表示当前要处理海拔 \(i\)，这一行可以接纳 \(j\) 个点，海拔 \(<i\) 的还有 \(k\) 个点没有填入的最小代价 \(f_{i,j,k}\)。
则可以有转移：\(f_{i,j+1,k}\gets f_{i,j,k}+\min\{C_x|H_x\le i\}\)，记 \(cnt_i=\#\{x|H_x=i\}\) \(f_{i+1,j,\max(k+cnt_i-j,0)}\gets f_{i,j,k}+K*(k+cnt_i)\)。
这样的时间复杂度是 \(O(n^2\max H_i)\) 的。
考虑 \(\max H_i\) 是 \(10^9\) 量级时，实际有操作意义的只有 \(H_i\) 和 \(H_i+1\) 这样的海拔，其他的海拔高度只影响第二种转移的权值计算，但是这个权值计算可以做到 \(O(1)\)。所以最终时间复杂度为 \(O(n^3)\)。
Day1 T3 Spy 3
很厉害的题目，首先考虑 \(q=1\) 怎么做。
我们找到一条从 \(0\) 到 \(T_0\) 的最短路，如果一个节点可以从多个节点走来，我们钦定从编号最小的走（为了唯一确定路径）。
在这条路径上，肯能会经过若干条边权 Bitaro 未知的边，我们将这些边标记为 1，其他边标记为 0。传输一个长度为 k 的字符串。
那么 Bitaro 将被标记了的边边权设置成 \(1\)，其余边设置成 \(+\infty\)。我们可以证明 Bitaro 选择出来的最短路径和 Aoi 的一致。
具体的，一条路劲的贡献可以被拆成两个部分，每一条边原来的权值-经过的未知边权值减小的量，发现 Aoi 选择的路径在第一个值中取到了最小值，在第二个值中取到了最大值，所以它一定是最优的。
考虑将这个做法拓展到 \(q>1\) 上。
这就意味着我们需要构造的不是最短路了，而是一个类似最短路树的结构。我们考虑依次处理 \(T_0,T_1\dots T_q\)。在处理 \(T_i\) 之前我们已经得到了 \(T_0\sim T_{i-1}\) 的最短路构成并了。如果我们知道 \(T_i\) 的最短路在什么时候和前面的最短路有交了，我们就可以从那个点开始，进行 \(q=1\) 的最短路了，因为这样每一条未知边最多只会被一个点的最短路覆盖，我们对于每一条未知边维护这个信息，就可以做到 \(k\log_2(q+1)+q\log_2n\)。更宽松的，我们可以将这个起始点向上移动到第一个未知边的下面，这样我们维护这个起始点就只需要 \(q\log_2(k+1)\)。考虑到 \(q+1=17\)，用 \(5\) 位维护太浪费了，所以压缩一下，即可通过。
Day2 T1 Board Game
我们首先分析一下 \(2\sim k\) 用处，因为要让 \(1\) 到达的时刻尽可能早，所以 \(2\sim k\) 需要走尽可能短的路径。考虑一个点走到了某一个终止点之后，它下一轮最多只需要走两步：\(u\to v\to u\)。所以除了第一轮，后面每一轮都最多走 \(2\) 步，代价可以被写成 \(2t+h\) 的形式。考虑走一步的时候，就是它在两个相邻的终止点之间横跳，假设我们可以在 \(a\) 轮，消耗 \(b\) 的时间走到一个这样的点，则它对应的代价就是 \((t-a)+b=t+(b-a)\)。可以证明在 \(t<a\) 的时候这个式子比 \(2t+h\) 劣，所以我们直接维护 \(b-a\) 即可。
而 \(h\) 和 \(b-a\) 的维护都是可以用 bfs 或者 01bfs 得到的。
因此，如果 \(1\) 每多走一轮，它就会至少多 \(k-1\) 的代价，也就意味相较于最早到达每一个点的轮数，最优的到达轮数至多比它对 \(\dfrac{n}{k-1}\)，我们可以建一个 \(O(\dfrac{n}{k-1})\) 层的分成图来求解，bfs 即可。看到对于 \(k\) 很大我们有了解决方案，就会联想到阈值分治。也就意味着我们有了 \(k>B\) 时 \(O(\dfrac{n^2}{B})\) 的做法。
考虑到 \(k\) 很小的时候，因为其他点的代价可以写成 \(kt+h\) 的形式，这也就意味着，最优的情况会形成一个下凸壳。我们对于每一种不同的斜率 \(k\)，钦定多走一轮的代价为 \(t\)，加上偏移量之后，一定只有在 \(t\) 属于对应斜率的区间才是最优的，所以可以直接跑 k 次 Dijk 来求解答案，时间复杂度 \(O(nB\log n)\)。
平衡之后复杂度为 \(O(n\sqrt{n}\log n)\)。
Day2 T3 Growing Vegetables is Fun 5
假设我们确定了每一种颜色的花盆对应的区间，我们可以通过调整法知道，必然是将 \(A\) 和 \(B\) 从小到大排序之后依次匹配。
由于 \([1,l)\cup [l+N,2N]\) 的处理可以认为是将所有的数取反了之后得到的结果，所以我们现在只考虑用 \(A[l,l+N-1],l\in [1,N]\) 去对应 \(B\) 的情况。
我们希望最大值最小，所以考虑二分答案 \(t\)。则对于每一个 \(A_i\)，我们知道它可以和一个区间的 \(B\) 匹配，具体的，就是 \([L,R)\)，其中 \(B_{L-1}< A_i-t\le B_L\)，\(B_{R-1}\le A_i+t<B_R\)。
由于 \(A\) 序列有极其特殊的结构，所以我们考察 \(A_i\) 的 \(l\in[1,N]\) 时，它会对应哪一个 \(B_j\)。
· 对于 \(i\in[1,N]\)，每一次移动区间会删去一个小于 \(A_i\) 的数，加入一个前若干次大于 \(A_i\) 后若干次小于等于 \(A_i\) 的数。对应的 \(B_j\) 中的 \(j\) 是一段斜率为 \(-1\) 的一次函数拼上一个常函数。
· 对于 \(i\in [N+1,2N]\)，每一次移动区间会加入一个小于 \(A_i\) 的数，删去一个前若干次小于等于 \(A_i\) 后若干次大于 \(A_i\) 的数。对应的 \(B_j\) 中的 \(j\) 是一段常函数拼上一个斜率为 \(1\) 的一次函数。
我们只需要计算出衔接的关键点，在配合上 \(A_i\) 能够匹配的 \(B\) 区间 \([L,R)\)，我们就可以 \(O(1)\) 计算出某一个区间的 \(l\)，对于这个 \(A_i\) 数满足条件的。我们利用差分前缀和就可以知道哪一些区间左端点 \(l\) 对于 \(N\) 个 \(A_i\) 满足条件了。
而计算关键点都是形如 \(\le A_i\) 的 \(x\) 最大的 \(A_x\) 之类的问题，可以通过指针扫一遍维护，单词 check 的时间复杂度为 \(O(n)\)。
所以最终时间复杂度为 \(O(n(\log n+\log \max A))\)。
Day3 T2 JOI Tour
为什么这道题平均分这么低，是不喜欢数据结构么qwq。
我不喜欢 \(0\) 下标，所以我处理的是 \((1,2,3)\)。
我们考虑能不能快速计算包含某一个点的所有 \((1,2,3)\) 点对数量，如果可以，我们只需要将这一个点以它原来的颜色的先减掉，然后再将它以现在的颜色加上。
如果 \(col_u=2\)，考虑任何的 1-3 都可以和 \(u\) 做贡献，除非他们在同一个子树里面。
记 \(cnt_{u,i}\) 为 \(u\) 子树内颜色 \(i\) 的点的数量，则答案即为 \(cnt_{1,1}\times cnt_{1,3}-\sum\limits_{v\in son_u}cnt_{v,1}cnt_{v,3}-(cnt_{1,1}-cnt_{u,1})(cnt_{1,3}-cnt_{u,3})\)。\(cnt_{u,*}\) 可以直接使用线段树维护。考虑直接维护 \(\sum\limits_{v\in son_u}cnt_{v,1}cnt_{v,3}\) 的值。
但是这样在修改的时候有一个对位加减的过程，难以维护。所以我们把重儿子挖掉。记轻儿子集合为 \(sson_u\)，重儿子为 \(bson_u\)，我们维护 \(\sum\limits_{v\in sson_u}cnt_{v,1}cnt_{v,3}\)。这样，修改一个节点的时候，只会修改到 \(O(\log n)\) 个 \(u\)，查询的时候只需要查 \(cnt_{u,1},cnt_{u,3},cnt_{bson_u,1},cnt_{bson_u,3}\) 即可。
计算一个二类点的权值就可以做到 \(O(\log n)\)，查询 \(cnt_{u,1},cnt_{u,3},cnt_{bson_u,1},cnt_{bson_u,3}\) 即可。
如果 \(col_u\in \{1,3\}\)，这两个是对称的，我们只考虑 \(1\)。
首先考虑不是 \(u\) 的祖先的点 \(v\)，如果 \(col_v=2\) 它做出的贡献是 \(cnt_{v,3}\)；对于它祖先的点，如果 \(col_v=2\)，其做出的贡献是 \(cnt_{1,3}-cnt_{son(v,u),3}\) 其中 \(son(v,u)\) 是 \(v\) 的是 \(u\) 祖先的儿子。
考虑直接维护对于所有 \(col_2=v\) 的点 \(cnt_{bson_v,3}\) 和 \(cnt_{v,3}\)。但是往上跳重链的时候，跳轻边要把特殊处理，时间复杂度 \(O(\log^2n)\)。
考虑修改，维护 dfn 在一个区间内的二类点的 \(cnt_{v,3},cnt_{bson_v,3}\) 的和，修改 2 类点的时候直接推平一个位置，修改 3 类点的时候每一次增加一条重链，可以区间加，查询是查询区间和。
总体时间复杂度为 \(O(n\log n+Q\log^2n)\)。
这不是我们铁人两项么，感觉可以加强到图上，可能要改一改然后处理一下就可以了。
Day3 T3 Tower
我们首先有一个很朴素的 DP \(f_i\) 表示走到第 \(i\) 个格子的最小代价。我们可以得到转移 \(f_i=\begin{cases}+\infty&,i\in[L_j,R_j]\\ \min(f_{i-1}+A,f_{i-D}+B)&,otherwise\end{cases}\)。
发现我们要么从 \(i-1\) 转移过来，要么从 \(i-D\) 转移过来，考虑将 \(i\) 表示成 \(xD+y,y\in[0,D)\) 的形式，则可以将上面的 DP 转移改写成： \(f_{x,y}=\begin{cases}+\infty&,Dx+y\in[L_j,R_j]\\\min(f_{x-1,D-1}+A,f_{x-1,y}+B)&,y=0\\ \min(f_{x,y-1}+A,f_{x-1,y}+B)&,otherwise\end{cases}\)，发现多出来了一种 \(y=0\) 的情况，但是无伤大雅。
对于这个二维 DP，扫描线 \(x\) 维，我们可以直接上 \(f_{x-1,*}\) 全局加 \(B\) 之后继承到 \(f_{x,*}\)，特殊修改 \(f_{x,0}\)，将被障碍限制住的位置设置成 \(+\inf\)，然后对于没有的限制住的位置，从左到右依次将 \(f_{x,y}\gets \min(f_{x,y},f_{x,y-1}+A)\)。
发现最后一步有一个加 \(A\)，拓展到整个序列上就是加一次函数，感觉很不美观，所以记 \(g_{x,y}=f_{x,y}-Ay\)，考虑维护 \(g\)，前面的部分都是相似的，只有最后一步是 \(g_{x,y}\gets \min(g_{x,y},g_{x,y-1})\)，所以这时我们需要将一个 \(g_{x,y}\) 更新，可以直接进行一次区间最小值的查询即可。
但是因为有障碍，所以每一层会被 \(g_{x,y-1}\) 更新的 \(g_{x,y}\) 会有很多，考虑能不能只维护那些关键的更新：
- 对于一个障碍，它能够做的事情就是让本来可以直接过去的点需要先走到 \(R_i+1\)，然后再跳过去，所以实际上每一次添加障碍之后，需要更新 \(R_i+1\) 对应的 \(g_{x,y}\)，这样的点有 \(O(Q)\) 个。
- 对于 \(g_{x,0}\gets g_{x-1,D-1}+DA\)，我们需要特殊维护第一个值和最后一个值，这样的点和 \(x\) 的取值数相同。
对于第二类关键点，它和我们扫描 \(x\) 的层数是有关的，但是如果直接暴力维护，层数会是 \(O(\dfrac{X}{D})\) 的，就爆掉了。但是考虑实际上有意义的层 \(x\)，只有每一个询问所在的层，以及每一个障碍所在的层的邻域。
直接使用线段树维护，时间复杂度为 \(O((n+Q)\log D)\)，将 \(y\) 维也离散化可以做到 \(O((n+Q)\log(n+Q))\)。
Day4 T1 Escape Route 2
卡了好长时间的常数，太唐氏了。
记 \(m=\sum M_i\)。
考虑如果我们确定了从 \(L\to L+1\) 坐哪一趟航班了，那么 \(L+1\to L+2\) 坐哪一趟航班就是固定的，一定是到达之后坐能做的最早到达的。这样就意味着我们可以枚举从 \(L\) 的哪一个航班出发。使用倍增可以做到 \(O(m\log n)\) 预处理 \(O(\log n)\) 查询，使用分块可以做到 \(O(m\sqrt{n})\) 预处理 \(O(1)\) 查询。
但是 \(M_L\) 很大的话就寄掉了，但是考虑我们也可以从 \(R\) 出发，倒推这个过程，所以我们单次查询的复杂度是 \(O(\min(M_L,M_{R-1})f)\) 的，\(O(f)\) 为单次求解复杂度。
对于相同的 \((L,R)\) 只做一次，考虑计算 \(\sum\min(M_L,M_{R-1})\) 的下界。如果查询的 \(\min(M_L,M_{R-1})\le B\) 的 \(M_i\) 我们可以直接处理，否则，\(M_L>B\) 的点只有 \(O(\dfrac{m}{B})\) 个，对所有这样点对做询问的复杂度 \(\le \sum\limits_{i=1}^B\dfrac{m}{B}M_i\le \dfrac{m^2}B\)，总时间复杂度为 \(O(nB+\dfrac{m^2}{B})\)，取 \(B=O(\dfrac{m}{\sqrt{n}})\) 可以得到询问次数上界为 \(O(m\sqrt{n})\)。
使用分块处理查询，时间复杂度为 \(O(m\sqrt{n}+n\sqrt{m})\)。
Day4 T2 Island Hopping
我们从小到大枚举点 \(i\)，我们按照距离从小到大询问点 \(u\)。如果 \(i\) 和 \(u\) 已经联通了，说明它们之间没有连边，同时距离 \(i\) 为 \(1\) 的点也都已经确定了；否则，由于 \(i\) 是从小到大枚举的，所以我们可以询问距离 \(u\) 第 \(\text{u的度数}+1\) 小的点，只有这个点为 \(i\)，才意味着 \(i\) 和 \(u\) 之间有连边。
这样每一个点被访问的次数是 \(d_i+1\) 次其中 \(d_i\) 是 \(i\) 点的度数。所以加起来共 \(3N-2\) 次，可以获得 \(65\) 分。
考虑我们直接暴力从小到大遍历距离 \(1\) 第 \(i\) 近的点，这一个点被遍历到时他的父亲也一定被遍历到了，如果我们之前没有访问过这个点，我们暴力从小到大访问距离他最近的点，直到访问到一个之前访问过的点为止（我们知道这个点就是它的父亲），我们和这些所有点连边即可。
暴力遍历所有的点需要 \(N-1\) 次询问，第二层遍历每一次询问对应一次连边，也是 \(N-1\) 次。所以最终只需要 \(2N-2\) 次即可。
Day4 T3 Table Tennis
我们考虑 \(n\) 个点的竞赛图有多少个环，考虑容斥，统计非三元环的数量，每一个非三元环必然对应一个点的两个出边，也就是非三元环数为 \(\dbinom{n}{3}-\sum\limits_{i=1}^n\dbinom{d_i}{2}\)，其中 \(d_i\) 为第 \(i\) 个点的出度。
由于 \(\dbinom{x}{2}\) 有很强的凸性，所以 \(d_i\) 一定是越均匀越好。发现 \(2\dbinom{x}{2}-1=\dbinom{x+1}{2}+\dbinom{x-1}{2}\)，这也就意味着，我们每一次找到两个出度相同的点 \(u,v\)，我们交换他们之间的变的方向，就可以使全局的三元环数 \(-1\)。而要使得所有点出度两两不同，那出度集合只能是 \(\{0,1,2\dots n-2,n-1\}\)，这是三元环的数量也就变成 \(0\) 了。
这是我们就有一个想法，我们从三元环数做多的局面开始，每一次找到一对出度相同的点，交换他们之间的边，知道三元环数变成 \(m\)。但是 \(n\) 个点的最多三元环数 \(c_n\) 是 \(O(n^3)\) 的。我们考虑找到 \(c_{n'}>=m\) 的最小的 \(n'\)，我们从它开始处理，因为 \(c_{n'}-c_{n'-1}\) 是 \(O(n'^2)\) 的，所以时间复杂度不劣于 \(O(n^2)\)。
考虑 \(c_i\) 等于多少，以及初始局面如何构造：
· 对于 \(2\nmid n\)，我们让每一个点的出度均为 \(\dfrac{n-1}{2}\)，构造为 \(i\) 向后 \(\dfrac{n-1}{2}\) 的点连边（超过 \(n\) 回到 \(1\)，也就是在环上）。
· 对于 \(2\mid n\)，我们让 \(\dfrac{n}{2}\) 的点度数为 \(\dfrac{n}{2}\)，让 \(\dfrac{n}{2}\) 的点度数为 \(\dfrac{n}{2}-1\)，构造为对于 \(i<=\dfrac{n}{2}\) 的点向后 \(\dfrac{n}{2}\) 个点连边，对于 \(i>\dfrac{n}{2}\) 的点向后 \(\dfrac{n}{2}-1\) 个点连边。
考虑交换，我们使用数据结构维护出度为 \(d_i\) 的点的集合，使用另一个数据结构维护大小 \(\ge 2\) 的所有集合，每一次取出并且修改即可，时间复杂度 \(O(\sum n^2)\) 或者 \(O(\sum n^2\log n)\)。
