CEOI 2022
Day1 T1 Abracadabra
首先将序列分割成 \([1,\frac{n}{2}]\) 和 \([\frac{n}{2}+1,n]\),考虑某一个序列的一个数 \(p_x\),如果它不是前缀最大值,则它必然和它的到前面距离它最近的前缀最大值 \(p_i\) 的这一段在一起处理。
证明考虑对于 \(p_i\) 如果被放进序列,说明另一堆有 \(t>p_i\),由于 \(p_i\) 时前缀最大值,但是 \(p_{i+1}\sim p_x\) 不是,则显然有 \(t>p_i>p_j,j=i+1,i+2\dots x\)。
这也就意味着,合并的过程可以看作将两个序列按照前缀最大值的位置开头分割成若干区间,然后以这些区间的第一个数的权值进行归并排序。
如果排序之后,\(\frac{n}{2}\) 和 \(\frac{n}{2}+1\) 之间刚好是分割开的,则进行一次分割不会影响这些区间的数量和结构,也就意味着序列不变。
由于每一次序列变化意味着增加了一个区间,所以有效的变换只有 \(O(n)\) 次。
使用平衡树维护区间,用线段树上二分快速求出区间第一个 \(>k\) 的数,即可维护这个过程。具体的:
首先进行第一次操作的初始化,然后将所有区间按照 \(\frac{n}{2}\) 的位置分裂,取出包含了 \(\frac{n}{2}\) 和 \(\frac{n}{2}+1\) 的区间(如果没有就意味着序列不会再变化),将其分成 \(\frac{n}{2}\) 及以前的这个区间,\(\frac{n}{2}\) 以后的区间按照前缀最大值分割成的若干区间,将其按照第一个数的权值插入原区间即可。
时间复杂度 \(O(N\log N+Q\log N)\)。
Day1 T2 Homework
考虑将操作树建出来。
考虑从上往下合并的过程,我们维护一个 DP 数组 \(f_{i,j}\),表示在 \(i\) 的子树内,第 \(j\) 小作为答案是否可行。
合并两个儿子 \(u,v\) 的时候,如果 \(f_{u,a}=f_{v,b}=1\),我们考虑它们会对哪些 \(f\) 做出贡献。
如果这个节点对应的操作是 \(\min\),则最小是 \(\min(a,b)\),也就是让较小的那个排在前面,最大是 \(a+b-1\),将所有 \(u\) 中 \(<a\) 的和 \(v\) 中 \(<b\) 都放在前面,下一个不是 \(a\) 就是 \(b\)。
如果这个节点对应的操作是 \(\max\),和上面的是完全对称的,最小是 \(a+b\),最大时 \(max(siz_u+b,siz_v+a)\)。
对于上面两种情况都可以证明最小值到最大值的区间内都可以取到。由此,我们可以用数学归纳法证明,对于任何一个节点 \(i\),为 \(1\) 的 \(f_{i,j}\) 构成一段区间,所以只维护区间的左右端点即可,时间复杂度 \(O(n)\)。
Day1 T3 Prize
考虑主动选择 \(K\) 个点,可以直接选择一个在第一棵树上包含根的大小为 \(K\) 的连通块。这样我们只需要处理出在第二棵树上的虚树即可。
现在的重点就是还原两颗虚树上的边权,由于第一棵树上没有额外的节点,所以我们优先考虑第二棵树,由于我们只能调用 \(K-1\) 次询问,而建虚树的过程也刚好需要 \(K-1\) 次求 lca 的操作,例如考虑二次排序建虚树,就是要对于 dfn 相邻的两个点求 lca,我们只需要对于这样的 \(K-1\) 对进行询问就可以还原出第二棵树上的边权。而在第一棵树上,发现这 \(K-1\) 次询问构成的路径会把整棵树联通,那么我们也是可以还原边权的。
在还原了边权之后,询问就很好处理了。
Day2 T1 Drawing
感觉很厉害的构造题。
我们想要使用链分治的方式构造,想要将这一个问题划分成两个子问题来实现。
假设我们处理的连通块及其对应的点集,同时有连通块内的一条极长链 \(A,B\),假设 \(A,B\) 已经确定了对应的点,而且还是点集对应凸包上的一条边。我们想要对于 \(A,B\) 链上的带权重心 \(C\) 找到点集中的这样一个点,是的 \(\Delta ABC\) 中不存在其他的点,然后将其他的点以 \(C\) 为中心极角排序,分成如下图的两个子问题:
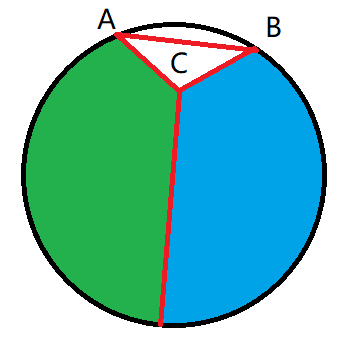
发现仍让满足 \(A,C\) 和 \(C,B\) 是凸包的一条边。由于是链分治,所以保证的复杂度,现在就是要考虑如何找到能够分割的点 \(C\)。
假设 \(A,C\) 之间的点的数量为 \(S_1\),\(B,C\) 之间的点的数量为 \(S_2\),则我们以 \(A\) 为中心极角排序,然后再后 \(S_2+1\) 个点中选择和 \(BA\) 夹角最小的点作为 \(C\)。可以证明这样的分界线一定能够使得蓝色和绿色的区域是凸的。
时间复杂度 \(O(n\log^2n)\)。
Day2 T2 Measures
显然,如果移动之后,如果有两个人的相对位置交换了一定不优,那么位置排序之后的顺序就是最终的顺序。
因为任何两个点之间都需要满足距离 \(\ge D\),那么我们认为对于某一对 \(i<j\),如果 \(x_j-x_i<D\times (j-i)\),则需要花 \(\dfrac{D(j-i)-(x_j-x_i)}{2}\) 的代价才能够使得 \(i,j\) 这一对数满足了对于 \(\ge D\) 的限制。
最终的答案就是 \(\max\limits_{i<j}\dfrac{D(j-i)-(x_j-x_i)}{2}\),可以直接用数据结构维护,时间复杂度 \(O((N+M)\log(N+M))\)。

