[COCI2013] hiperprostor 题解

前言

题目链接：Hydro & bzoj；黑暗爆炸。

题意简述

\(n\) 个点 \(m\) 条边的有向图上，第 \(i\) 条边的边权被表示为 \(k_i x + b_i\)，其中 \(x\) 为一正整数。有 \(q\) 次询问，求出当 \(x\) 取值不同时，\(S\) 到 \(T\) 最短路的值有多少种，以及和为多少。如果最短路的值有无限种可能，输出 inf。可能不能从 \(S\) 到达 \(T\)。

\(n \leq 500\)，\(m \leq 10000\)，\(q \leq 10\)，\(0 \leq b_i \leq 10^6\)，\(0 \leq k_i \leq 10\)。

原题 \(k_i \in \{ 0, 1 \}\)，且 \(k_i = 1\) 时，\(b_i = 0\)。

题目分析

询问很少，只要不太离谱的做法应该都是正确的。考虑一次询问，很容易想到分层图跑最短路。对 \(x\) 前面的系数分层，求出 \(dis_{k, u}\) 表示 \(x\) 前的系数为 \(k\) 时，走到 \(u\) 的最短路的常数项，即此时最短路为 \(kx + dis_{k, u}\)。

注意到，\(k\) 不是无上界的，一个可能取到的上界为所有边的 \(k_i\) 之和，另一个取不到的上界是走了 \(n\) 条最大的边，不妨将其记作 \(K = \min \{ \sum \limits _ {i = 1} ^ m k_i, n \max k_i \}\)。

不妨先考虑什么时候无解。此时一定有 \(\forall k \in [0, K], dis_{k, T} = \infty\)。

以及无穷解。此时 \(S\) 到 \(T\) 的最短路完全依赖于 \(x\) 的值。换句话说，不能不经过一条含有 \(x\) 的边到达 \(T\)，即 \(dis_{0, T} = \infty\)。

对于 \(T\) 来说，对于每一个 \(dis_{i,T} \neq \infty\) 的 \(i\)，我们有直线 \(f_i(x) = i x + dis_{i, T}\)。将这些直线在平面直角坐标系中绘出，对于一个 \(x\) 的取值，我们找到 \(\min f_i(x)\) 就是此时最短路长度。将所有 \((x, \min f_i(x))\) 连起来，就构成了一个上凸包。容易发现，凸包的边数是 \(\mathcal{O}(K)\) 的。

（你是不是感觉最上面那条线是倾斜的？其实它是水平的。我还怀疑这图怎么会画错了呢。）

如何求解放到之后讲，先来说说怎么统计答案。我们发现，在凸包两个相邻的拐点之间，其实是算一个一次函数在这段区间的函数值之和，是个等差数列，可以 \(\Theta(1)\) 计算。

剩下是求解凸包过程。平常我们的凸包是对着点集搞的，而这次是求出一堆直线围成的凸包，所以会有些不一样。考虑从大到小枚举直线的斜率，类似点集，维护一个单调栈，栈中的就是目前凸包中的直线，考虑新增一条直线的过程，什么时候栈顶直线不可能成为凸包的一部分呢？

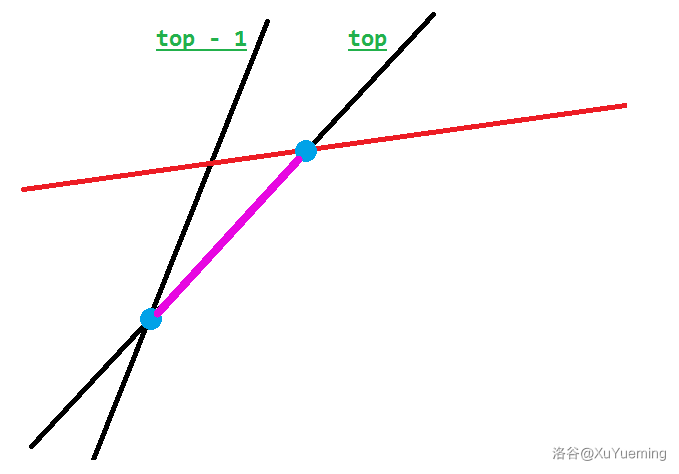
我们发现，在紫色这一段区间内，栈顶直线仍然是凸包的一部分。

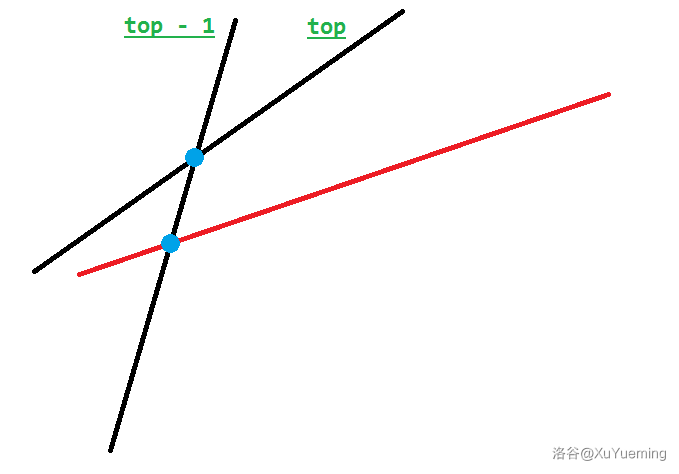
此时，栈顶直线已经毫无用处了，因为在 \(top - 1\) 之后，新增直线永远比 \(top\) 更优。读者已经发现了，在直线交点处我们用蓝色做了标记，如果新增直线和 \(top\) 的交点在 \(top\) 和 \(top - 1\) 的交点右侧，说明在这两个交点间，\(top\) 是凸包的一部分，反之则要弹出栈顶。

事实上，这和决策单调性有着异曲同工之妙。在决策单调性时，我们二分出 \(i\) 比 \(j\) 更优的第一个位置，相当于我们这次求出的直线交点，弹栈操作也是换汤不换药的。

如此，在一个询问内我们可以做到 \(\Theta(Kn \log m)\) 的时间复杂度。

代码

#include <cstdio>
#include <iostream>
#include <cstring>
#include <sstream>
#include <queue>
#include <set>
using namespace std;

int n, m, q;

struct Graph {
    struct node {
        int to, w1, w2, nxt;
    } edge[10010 << 1];
    int tot, head[520];
    void add(int u, int v, int w1, int w2) {
        edge[++tot] = { v, w1, w2, head[u] };
        head[u] = tot;
    }
    inline node & operator [] (const int x) { return edge[x]; }
} xym;

int dis[10010][520];

int totX;

template <typename T>
using minHeap = priority_queue<T, vector<T>, greater<T>>;

using lint = long long;

lint cnt, sum;

inline lint solve(int k, int b, int x) {
    // 计算一次函数值
    return 1ll * k * x + b;
}

inline void solve(int k, int b, int l, int r) {
    // 计算一次函数在 [l, r] 的函数值之和
    l = max(l, 1);
    if (l > r) return;
    cnt += r - l + 1;
    sum += (solve(k, b, l) + solve(k, b, r)) * (r - l + 1) / 2;
    // 等差数列
}

inline double jiao(int k1, int b1, int k2, int b2) {
    // 两直线交点
    return 1.0 * (b2 - b1) / (k1 - k2);
}

inline int jjiao(int k1, int b1, int k2, int b2) {
    // 最大的小于两直线交点横坐标的整数
    return max(0, (b2 - b1 - 1) / (k1 - k2));
}

int s, t;
int hill[520], tot;

inline double jiao(int a, int b) {
    return jiao(a, dis[a][t], b, dis[b][t]);
}

signed main() {
    scanf("%d%d", &n, &m);
    for (int i = 1, u, v, w1, w2; i <= m; ++i) {
        static char str[10];
        scanf("%d%d%s", &u, &v, str);
        if (*str == 'x') {
            w1 = 1, w2 = 0;
            ++totX;
        } else {
            stringstream sin(str);
            sin >> w2, w1 = 0;
        }
        xym.add(u, v, w1, w2);
    }
    totX = min(totX, n);
    scanf("%d", &q);
    for (; q--;) {
        scanf("%d%d", &s, &t);

        #ifdef XuYueming
        printf(">>>>>>>>>>> ");
        #endif

        if (s == t) {
            printf("1 0\n");
            continue;
        }
        memset(dis, 0x3f, sizeof dis);
        dis[0][s] = 0;
        minHeap<pair<int, pair<int, int>>> Q;
        Q.push({ 0, { 0, s } });
        while (!Q.empty()) {
            auto [ndis, _now] = Q.top();
            Q.pop();
            auto [xcnt, now] = _now;
            if (now == t || ndis > dis[xcnt][now] || xcnt > totX)
                continue;
            for (int i = xym.head[now]; i; i = xym[i].nxt) {
                int tx = xcnt + xym[i].w1;
                int len = dis[xcnt][now] + xym[i].w2;
                int to = xym[i].to;
                if (dis[tx][to] > len) {
                    dis[tx][to] = len;
                    Q.push({ len, { tx, to } });
                }
            }
        }
        
        bool can = false;
        for (int i = 0; !can && i <= totX; ++i)
            can |= dis[i][t] != 0x3f3f3f3f;
        if (!can) {
            puts("0 0");
            continue;
        }
        if (dis[0][t] == 0x3f3f3f3f) {
            puts("inf");
            continue;
        }
        
        // 有若干形如 f_i(x) = ix + dis[i][t] 的直线
        // 将这些直线在平面直角坐标系中绘出。
        // 对于一个 $x$ 的取值，我们找到 $\min f_i(x)$ 就是此时最短路长度
        // 将所有 $(x, \min f_i(x))$ 连起来，就构成了一个上凸包。
        
        tot = 0;
        for (int i = totX; i >= 0; --i) if (dis[i][t] != 0x3f3f3f3f) {
            while (tot - 1 >= 1 && jiao(hill[tot - 1], hill[tot]) >= jiao(hill[tot], i))
                --tot;  // 此时栈顶直线不可能成为凸包的一部分，类似于决策单调性
                        // 直线交点就是 i 比 j 更优的第一个位置
            hill[++tot] = i;  // 把这条直线加入凸包
        }
        
        cnt = 1, sum = dis[0][t];
        for (int i = 1, lst = 1; i + 1 <= tot; ++i) {
            // 计算 [上一次交点, 这一次交点) 的函数值之和
            int cur = jjiao(hill[i], dis[hill[i]][t], hill[i + 1], dis[hill[i + 1]][t]);
            // 求出小于交点横坐标的最大整数
            solve(hill[i], dis[hill[i]][t], lst, cur);
            lst = cur + 1;  // 更新上一次交点
        }
        printf("%lld %lld\n", cnt, sum);
    }
    return 0;
}