Temperature 题解

前言

题目链接：洛谷；SPOJ；Hydro & bzoj。

题意简述

有一个长度为 $n$ 的序列，每个位置值的范围为 $[L_i,R_i]$ 内，求原序列可能的最长不降子串长度。

题目分析

尝试找一些性质。发现，连续一段合法的区间，都能分成若干真正参与最长不降子串，以及紧跟着的若干包含 $L_i$ 的位置。下图红色表示前者，黑色表示后者。

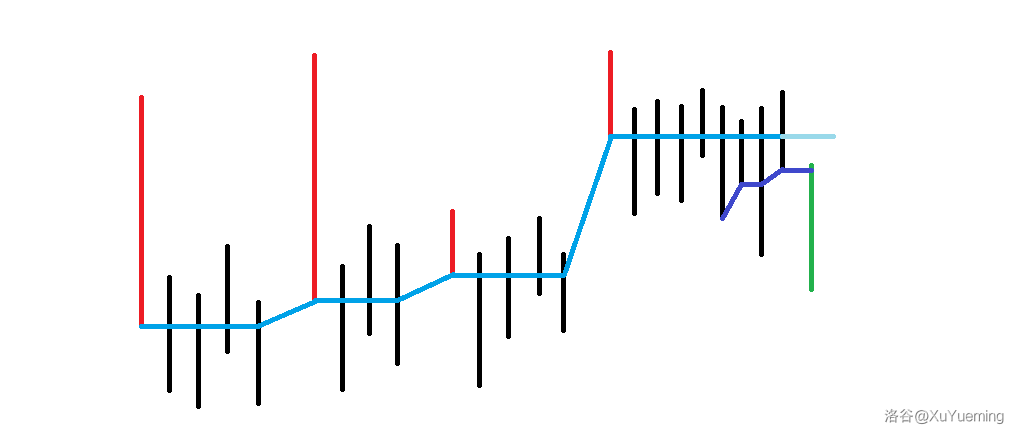
我们把右端点向右移动，左端点肯定不会向左移动，是一个双指针。我们记 $l$ 是当前左端点，现在让 $r\leftarrow r+1$，看看左端点如何变化。发现不够，还要记 $lst$ 表示上一个出现红色段的位置。那么分为以下几个情况讨论。

1. $L_r\le L_{lst}\le R_r$：
   说明这是一个黑色段，不需要任何操作。
2. $L_r\ge L_{lst}$：
   说明遇到了一个新的红色段，贡献了最长不降子串，让 $lst\leftarrow r$。
3. 此时必有 $R_r<L_{lst}$：
   说明遇到上图绿色段的情况。我们要在 $lst+1\sim r$ 里重新挑选出一个 $l^{\prime }$ 和 $ls{t}^{\prime }$。

前两者都很好处理，思考怎么弄第 $3$ 条。

发现关键都在每条线段的下端，如果 $l\sim r$ 里 $max{L}_i>R_r$，那么一定是不合法的，因为是不能下降的。所以考虑用 ST 表维护区间最小 $L$ 的位置。遇到情况 $3$，先让 $l^{\prime }\leftarrow lst$，当 $max{L}_{l^{\prime }\sim r}>R_r$，将 $l^{\prime }\leftarrow l^{\prime }+1$，至于 $ls{t}^{\prime }$，就是最终 $max{L}_{l^{\prime }\sim r}$ 的那个位置。

时间复杂度 $\mathrm{\Theta }(n\log n)$，瓶颈在于 ST 表。

继续思考，发现合法区间 $l\sim r$ 的充要条件也是 $\mathrm{\forall }i\in [l,r],max{L}_{l\sim i}\le R_i$。那么不需要那么麻烦，直接上双指针。如果 $max{L}_{l\sim r}>R_r$，$l\leftarrow l+1$。正确性显然。但是时间复杂度还是 $\mathrm{\Theta }(n\log n)$，能不能去掉 ST 表呢？

发现，我们要维护滑动窗口的最值，所以，上单调队列。队列里 $L$ 从大到小排序。统计答案时，上一次弹出队列的位置 $+1$ 就是合法的最长的左端点。

时空都是线性的。

代码

// #pragma GCC optimize(3)
// #pragma GCC optimize("Ofast", "inline", "-ffast-math")
// #pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
using namespace std;
 
int n, L[1000010], R[1000010];
int Q[1000010], head = 1, tail;
int ans = 1;
 
signed main() {
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) scanf("%d%d", &L[i], &R[i]);
    for (int i = 1; i <= n; ++i) {
        while (head <= tail && L[Q[head]] > R[i]) ++head;
        if (head <= tail) ans = max(ans, i - Q[head - 1]);
        while (head <= tail && L[Q[tail]] <= L[i]) --tail;
        Q[++tail] = i;
    }
	printf("%d", ans);
	return 0;
}

后记 & 反思

双指针，考虑好添加右端点后，怎么删去不合法的左端点。