[CEOI2011] Matching 题解
前言
题目链接:洛谷。
在上一题之后,模拟赛又放了一道 KMP 重定义相等的问题,但是寄了,故再记之。
题意简述
现在给出 \(1 \sim n\) 的排列 \(p\) 和序列 \(h_1, h_2, \cdots, h_m\),请你求出哪些 \(h\) 的子串符合排列 \(p\)。串 \(a_i\) 符合一个排列被定义为其从小到大排序后得到 \(a_{p_i}\)。
题目分析
先想到定义 \(b_{p_i} = i\),那么一个串符合 \(p\),等价于其每个值的排名与 \(b_i\) 相等。
也是考虑,用相对信息来进行匹配。很容易想到,如果对于两个串,每个位置的前驱后继都相等,这两个串是符合上述“符合”的定义的。因为每个数都能够确定在排名中唯一的位置。
由于 KMP 匹配的过程是从左往右扫的过程,我们如果要记相对信息,只能记这个位置和之前位置的相对关系。这是对于 KMP 重定义匹配普遍的结论。这是为什么呢?
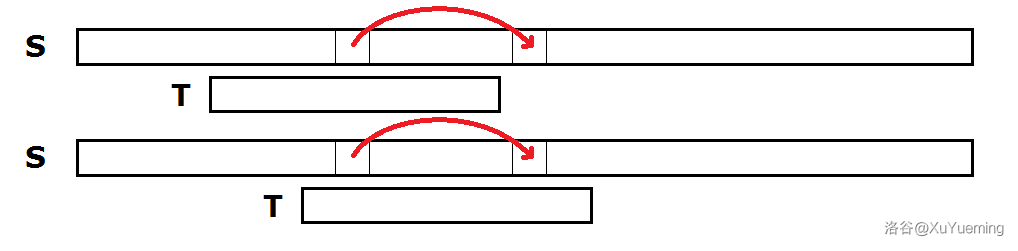
比如,之前我们有一个位置和后面的相对信息超出了当前匹配的范围,我们当做它不存在。但是,随着我们向右扫描的过程中,这个位置可能有被包含了进来,就有可能不符合要求。相反,如果我们记录左边的信息,如果超出范围,就不可能再被包含进来,所以不会出现以上情况。
那我们如何设计新的信息呢?我们假设之前匹配到的位置都暂时符合排名关系,那要新增一个值,让这个值也符合排名位置。这是一个类似于在一个有序的数列里面插入一个值,使得这个值插入的位置满足给出的信息。想到,对于 \(b\) 可以预处理出 \(L_i\) 和 \(R_i\) 分别表示 \(i\) 与在 \(1 \sim i - 1\) 中的前驱后继之差。这也和我们要插进去的位置相关。
所以,假设当前位置为 \(i\),\(i - 1\) 匹配到的位置为 \(j\),我们只需要判断 \(S[i - L[j + 1]] < S[i] < S[i + R[j + 1]]\) 就表示可以插到对应位置,满足要求。当然,如果 \(L[j + 1]\) 或 \(R[j + 1]\) 不存在则无需判断。
至于预处理 \(L\) 和 \(R\),由于 \(b\) 是排列,所以倒序枚举,链表查前驱后继并删去当前数即可。
时间复杂度为 \(\Theta(n + m)\)。
代码
略去了快读快写,是最优解。
// #pragma GCC optimize(3)
// #pragma GCC optimize("Ofast", "inline", "-ffast-math")
// #pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <cstdio>
using namespace std;
int n, m;
int xym[1000010], yzh[1000010];
int whr[1000010], fail[1000010];
int L[1000010], R[1000010];
int pre[1000010], nxt[1000010];
int ans[1000010], tot;
inline bool check(int *yzh, int x, int y) {
return (!L[x] || yzh[y + L[x]] < yzh[y]) && (!R[x] || yzh[y + R[x]] > yzh[y]);
}
signed main() {
fread(buf, 1, MAX, stdin), read(n), read(m);
for (int i = 1; i <= n; ++i) {
read(whr[i]), xym[whr[i]] = i;
pre[i] = i - 1, nxt[i] = i + 1;
}
for (int i = n; i; --i) {
if (pre[xym[i]] ) L[i] = whr[pre[xym[i]]] - i;
if (nxt[xym[i]] <= n) R[i] = whr[nxt[xym[i]]] - i;
pre[nxt[xym[i]]] = pre[xym[i]];
nxt[pre[xym[i]]] = nxt[xym[i]];
}
for (int i = 1, j = fail[0] = -1; i <= n; ++i) {
while (~j && !check(xym, j + 1, i)) j = fail[j];
fail[i] = ++j;
}
for (int i = 1; i <= m; ++i) read(yzh[i]);
for (int i = 1, j = 0; i <= m; ++i) {
while (~j && (j == n || !check(yzh, j + 1, i))) j = fail[j];
if (++j == n) ans[++tot] = i - n + 1;
}
write(tot), putchar('\n');
for (int i = 1; i <= tot; ++i) write(ans[i]), putchar(' ');
fwrite(obuf, 1, o - obuf, stdout);
return 0;
}
本文作者:XuYueming,转载请注明原文链接:https://www.cnblogs.com/XuYueming/p/18319599。
若未作特殊说明,本作品采用 知识共享署名-非商业性使用 4.0 国际许可协议 进行许可。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号