[CEOI 2013] 千岛之国 / Adritic 题解

前言

题目链接：洛谷。

题意简述

你被困在一个被划分为 \(2500 \times 2500\) 的二维平面内！平面上有 \(n\)（\(n \leq 250000\)）个岛屿你可以停留，你可以在这些岛屿之间行走，但是你只能走到严格在当前岛屿的左上或右下的岛屿。即目标点 \((x', y')\) 满足和当前点 \((x, y)\) 的关系为：\((x' < x \land y' < y) \lor (x' > x \land y' > y)\)。问分别从每个岛屿出发，分别走到其他岛屿的最小步数之和是多少。

题目分析

你当然可以暴力建图加分别跑 BFS，时间复杂度 \(\Theta(n ^ 3)\)。优化？难道说扫描线的同时线段树优化建图再然后 01-BFS？似乎这样变得更劣、更难继续优化了？不太行。所以考虑换一个思路。

发现平面边长是 \(2500\)，在引导我们思考有关平面边长的平方的算法。

经过玩样例发现，不能直接一步走到的地方是左下角和右上角的一片区域。并且这两片区域会越来越小，直到里面一个岛屿都没有了后停止。

比如从 \((4, 5)\) 出发，用灰色区域表示能够直接一次走到的区域。即从当前 \(k\) 步之内能到达的区域，使用 \(k + 1\) 步能够到达的区域。

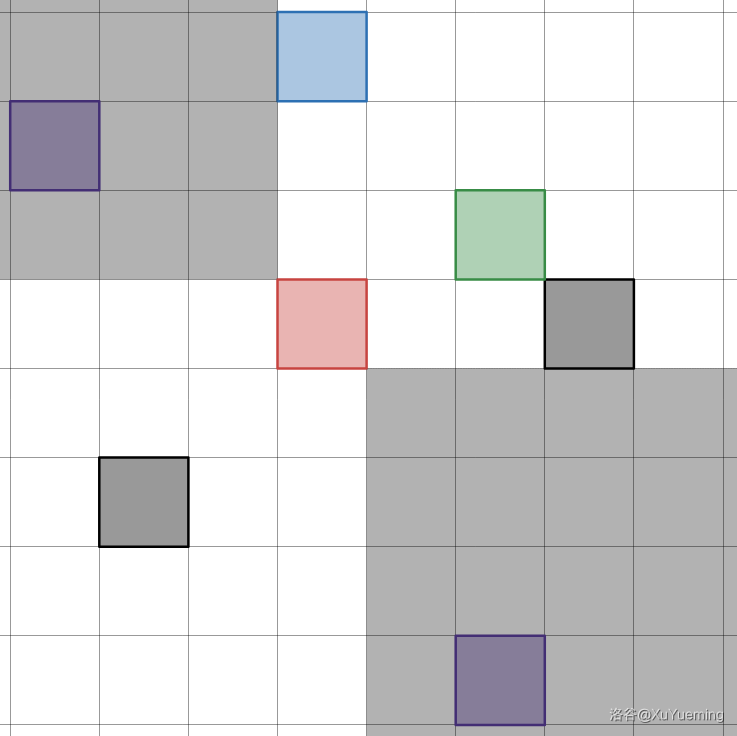
然后继续，接下来能够直接一次走到的区域，也即走 \(2\) 步及以内能到达的区域。

发现 \(2\) 步以内就能走到所有岛屿。过程中，没有被灰色覆盖的区域就是所谓的“不能直接一步走到的区域”。这个逐渐减少的过程也很好理解。

那么，状态就可以记这两个区域了。发现两个区域互相独立，所以可以分别计算。并且发现，在计算步数时，每次加上当前不能一次走到的区域的个数就行了，这相当于把某一个区域对答案的贡献拆到了每走一步里。注意初始每个位置至少需要 \(1\) 步，以及不要把起点算进去。这个式子在下面会列出来。

设 \(f[x][y]\) 表示当前不能一次走到的区域是以 \((x, y)\) 为右上角的区域，里面的区域对答案的贡献。同理，\(g[i][j]\) 表示当前不能一次走到的区域是以 \((x, y)\) 为左下角的区域，里面的区域对答案的贡献。

如果起点是 \((x, y)\)，上面我们讲的答案就是 \((n - 1) + (f[x][y] - 1) + (g[x][y] - 1)\)。

那该如何转移呢？以左下角的 \(f[x][y]\) 为例。

首先，我们要知道这一片区域内岛屿的数量，二维前缀和即可。其次，我们要知道下一个状态。我们要在这个区域的右边能够到达的区域里，找到最下方的一个岛屿，下一个状态的纵坐标就是这个岛屿的纵坐标。以及在上方能够到达的区域里，找到最左边的一个岛屿，作为下一个状态的横坐标。可以结合上面的样例理解。这个可以用前后缀最值预处理。

实现的时候，用一个记忆化搜索就行了。不知道为什么有题解说要特判 \(n = 1\)，不特判也能过。

代码

略去了快写。

#include <cstdio>
#include <cstring>
using namespace std;

int n, x[250010], y[250010];
bool on[2510][2510];
int sum[2510][2510];
int mini[2510], minj[2510];
int maxi[2510], maxj[2510];

inline int min(int a, int b) {
	return a < b ? a : b;
}

inline int max(int a, int b) {
	return a > b ? a : b;
}

int ur(int x, int y) {
	static int f[2510][2510];
	static bool vis[2510][2510];
	if (vis[x][y]) return f[x][y];
	vis[x][y] = true;
	if (sum[x][2500] - sum[x][y - 1] == 0) return 0;
	return f[x][y] = sum[x][2500] - sum[x][y - 1] + ur(min(x, mini[y - 1]), max(y, maxj[x + 1]));
}

int dl(int x, int y) {
	static int f[2510][2510];
	static bool vis[2510][2510];
	if (vis[x][y]) return f[x][y];
	vis[x][y] = true;
	if (sum[2500][y] - sum[x - 1][y] == 0) return 0;
	return f[x][y] = sum[2500][y] - sum[x - 1][y] + dl(max(x, maxi[y + 1]), min(y, minj[x - 1]));
}

signed main() {
	fread(buf, 1, MAX, stdin);
	read(n);
	memset(mini, 0x3f, sizeof mini);
	memset(minj, 0x3f, sizeof minj);
	for (int i = 1; i <= n; ++i) {
		read(x[i]), read(y[i]), on[x[i]][y[i]] = true;
		mini[y[i]] = min(mini[y[i]], x[i]);
		maxi[y[i]] = max(maxi[y[i]], x[i]);
		minj[x[i]] = min(minj[x[i]], y[i]);
		maxj[x[i]] = max(maxj[x[i]], y[i]);
	}
	for (int i = 1; i <= 2500; ++i) {
		mini[i] = min(mini[i], mini[i - 1]);
		minj[i] = min(minj[i], minj[i - 1]);
	}
	for (int i = 2500; i; --i) {
		maxi[i] = max(maxi[i], maxi[i + 1]);
		maxj[i] = max(maxj[i], maxj[i + 1]);
	}
	for (int i = 1; i <= 2500; ++i)
	for (int j = 1; j <= 2500; ++j)
		sum[i][j] = on[i][j] + sum[i][j - 1] + sum[i - 1][j] - sum[i - 1][j - 1];
	for (int i = 1; i <= n; ++i) {
		write(n + (ur(x[i], y[i]) - 1) + (dl(x[i], y[i]) - 1) - 1);
		putchar('\n');
	}
	fwrite(obuf, 1, o - obuf, stdout);
	return 0;
}

后记 & 反思

对对对，扫描线的同时线段树优化建图再然后 01-BFS 发现无从下手的人就是我。

这道题转化模型、寻找性质，以及拆贡献的方法，对我们有诸多启示。