[USACO22FEB] Paint by Rectangles P 题解

前言

没用线段树的小常数、小短码。

题目链接：洛谷。

题意简述

给出 $n$ 个平行于坐标轴的矩形，各边所在直线互不重合，钦定最外面为白色，对这个平面图黑白染色，分别求黑色块数和白色块数。

题目分析

这道题扫描线一眼题吧？所以考虑从左到右扫描线。初始白色有 $1$ 块。

我们发现，在扫描线的任意时刻，这个序列一定是类似斑马线黑白交错出现的。我们如果确定了这个序列某一端的颜色，以及有多少个颜色段，我们就能唯一确定这个序列，方便我们统计答案。

加边

先考虑加边。加入一条竖边 $[l,r]$，就把这段区间异或一下，统计新增的白色块数和黑色块数。根据一开始的分析，我们需要知道这条边对应的区间有多少个颜色段，以及这个区间下面第一块的颜色是什么就行了。

记有 $cnt$ 个块，黑色为 $1$，白色为 $0$，记最下面一块颜色是 $c\in \{0,1\}$。

那么就让 $c$ 的块数加上 $\lceil \frac{cnt}{2}\rceil$；让 $c\mathrm{xor}1$ 的块数加上 $\lfloor \frac{cnt}{2}\rfloor$。

那么如何知道块数和最下面的颜色呢？使用树状数组维护即可。

我们维护横边。加边的时候用树状数组将 $l,r$ 分别单点加一。那么块数就是 $[l+1,r-1]$ 中横边个数加一；最下方的颜色就查询 $l$ 以下有多少条横边，若是奇数个，则是白色，反之是黑色。

可以跟着作者模拟样例加深理解

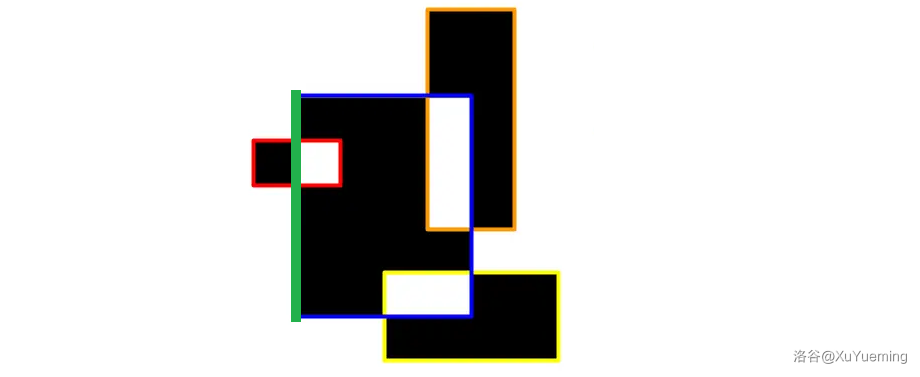
加入这条绿色的竖边。块数 $cnt=3$，由于 $l$ 下方横边数量 $0$ 是偶数，所以最下方颜色是黑色。就上黑色块数加上 $\lceil \frac{3}{2}\rceil =2$，白色块数加上 $\lfloor \frac{3}{2}\rfloor =1$。

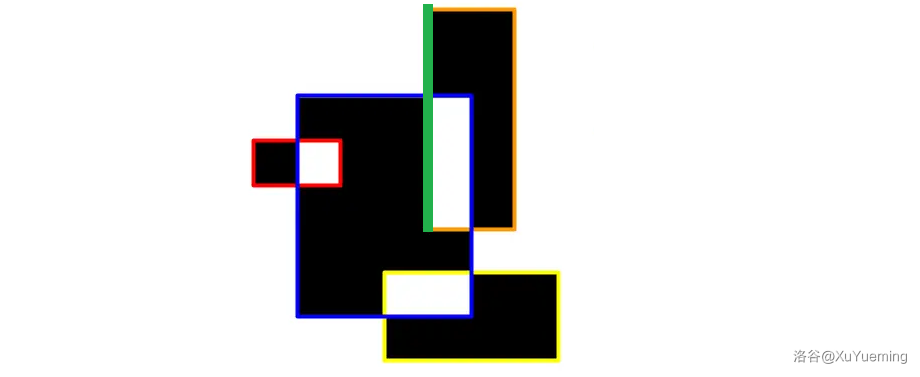
再来看看这条绿边。块数 $cnt=2$，由于 $l$ 下方横边数量 $3$ 是奇数，所以最下方颜色是白色。就上黑色块数加上 $\lceil \frac{2}{2}\rceil =1$，白色块数加上 $\lfloor \frac{2}{2}\rfloor =1$。

删边

删边也同理，但是略有不同。记删边后，这里有 $cnt$ 个块，最下面一块颜色是 $c\in \{0,1\}$。

注意，如果此时 $cnt=1$，则表示这是一条「结束的边」。之前我们将 $c$ 统计成多个块，但这时候它们到一起去了，所以要将 $c$ 的块数减一。

其他情况注意最下面的颜色是和加边相反的，以及最上面的块和最下面的块是和外面的连成一个块，不做统计。

结合样例更好理解

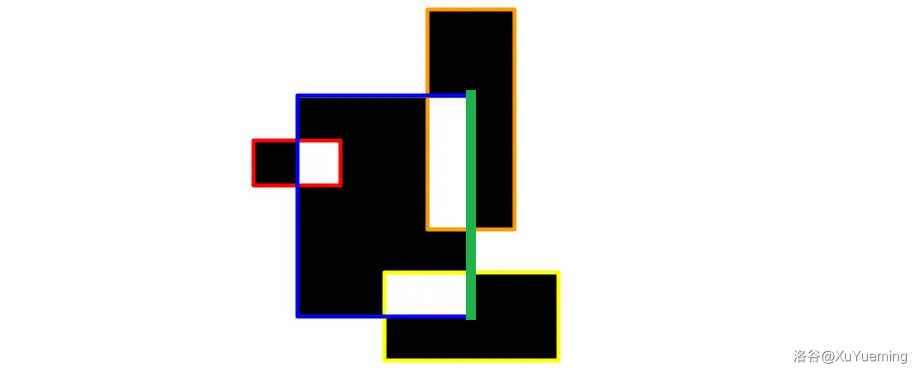
删去这条绿色的边。$l$ 下面横边数量 $1$ 是奇数，所以最下方颜色是黑色（而不是白色）。块数 $cnt=3$，但是最上面的黑色块属于橙色矩形，最下面的黑色块属于黄色矩形，这些块之前已经统计过了。所以让黑色块数加上 $\lfloor \frac{cnt-2}{2}\rfloor =0$，白色块数加上 $\lceil \frac{cnt-2}{2}\rceil =1$。

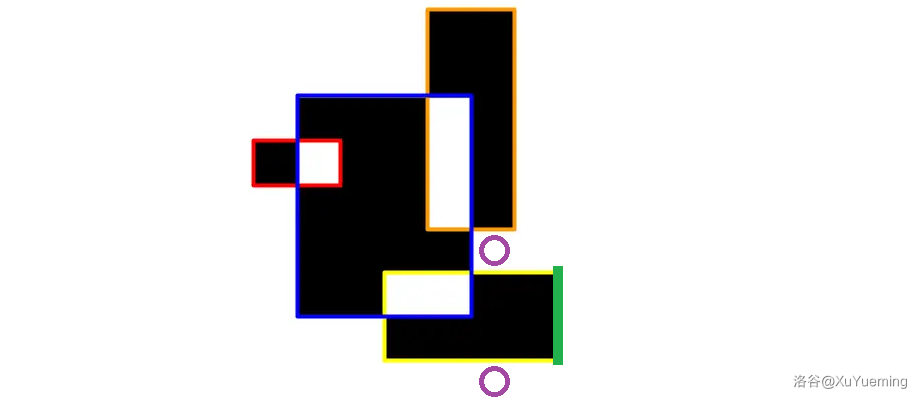
删去这条绿色的边，即为前文提到的「结束的边」。$l$ 下面横边数量 $0$ 是偶数，所以最下方颜色是白色。这种情况特殊在，两个紫色圆圈处，我们将它统计成两个白色部分，而实际上它是一个块，可以理解为在这里将它们合并了，所以将白色块数减一。

处理

这样就结束了吗？不不不，你可以看看下面的最简单的反例。

没错，只有一个矩形。我们会发现在删去右边的竖边时，不应该将白色块数减一。

这是为什么呢？我们发现这是因为白色是「背景」，本来就连在一起了。

那我们将白色块数加上矩形互相相交形成的连通块个数就行了，吗？但是还是不对，不光光只是外面的白色平面，我们考虑矩形完全包含的情况。

我们发现，处理里面红色矩形的时候，也会将黑色块数多减了一。此时，由于红色矩形和紫色矩形没有任何交点，也即不和紫色矩形相交，相当于红色矩形处在一个背景色是黑色的平面内，这是一个更小的子问题。

所以，我们在开始处理一个矩形互相相交的连通块时，首先看看它是处在一个黑色还是白色的平面内，将这个颜色数量加一，然后再处理这个子问题，这样就不会出现问题。

那么我们在预处理的时候，需要用并查集把相交的矩形合并起来。还是考虑扫描线的过程，对于一条竖边（无论是矩形左边还是右边），我们需要把此时依然存在的横边中，和竖边有交的那一部分对应的矩形，和这个竖边对应的矩形合并。发现由于我们做区间合并，序列被我们划分成了若干个连通块，每个连通块都被并查集合并到一起了。显然为了减少重复操作，我们对这样的连通块只用做一次就行了。于是可以用类珂朵莉树状物实现就行了。

时间复杂度 $\mathcal{O}(n(\log n+\alpha (n)))$。

代码

参考代码内注释可以帮助更好理解。

不压行，去掉注释仅 $110$ 行左右，其中还包含了很多空行，和 $21$ 行的树状数组板子。

#include <iostream>
#include <cstdio>
#include <set>
using namespace std;
 
const int N = 100010;
 
int n, T;
 
int L[N << 1], R[N << 1];
// L[i] ~ R[i] 是横坐标为 i 的竖边
 
int toleft[N << 1], bl[N << 1], p[N << 1];
// toleft[i] 是将一个矩形右边的竖边映射到左边的竖边
// bl[i] 是一个左边的竖边所在矩形的编号
// p[i] 是一条横边所对应的左边的竖边编号
 
struct node {
    mutable int l, r, cnt, who;
	// who 表示这一段区间在并查集上祖先都是 who
    inline friend bool operator < (const node& a, const node& b) {
        return a.l < b.l;
    }
};
// 这里的 cnt 用来优化常数
// 每次使用 yzh.query(l, r) 也是正确的
 
set<node> S;
// 用 set 维护目前出现的所有横边
// 一个 node 里都被 merge 成了一个连通块
using Iter = decltype(S.begin());
 
struct Bit_Tree {
    constexpr inline int lowbit(const int x) {
        return x & -x;
    }
    int tree[N << 1];
    inline void modify(int p, int v) {
        for (int i = p; i <= n; i += lowbit(i)) tree[i] += v;
    }
    inline int query(int p) {
        int res = 0;
        for (int i = p; i; i -= lowbit(i)) res += tree[i];
        return res;
    }
    inline int query(int l, int r) {
		--l;
		int res = 0;
		for (; r > l; r -= lowbit(r)) res += tree[r];
		for (; l > r; l -= lowbit(l)) res -= tree[l];
		return res;
    }
} yzh;
// 简单树状数组
 
int fa[N];
bool vis[N];
int get(int x) { return fa[x] == x ? x : fa[x] = get(fa[x]); }
void merge(int a, int b) { fa[get(a)] = get(b); }
// 并查集维护矩形连通性
 
signed main() {
    scanf("%d%d", &n, &T);
    for (int i = 1, x1, y1, x2, y2; i <= n; ++i) {
        scanf("%d%d%d%d", &x1, &y1, &x2, &y2);
        L[x1] = L[x2] = y1, R[x1] = R[x2] = y2;
        toleft[x2] = p[y1] = p[y2] = x1, bl[x1] = i, fa[i] = i;
    }
    n <<= 1;
    for (int i = 1; i <= n; ++i) {
		if (!toleft[i]) {
			static auto insert = [] (int x, int k) -> void {
				auto it = S.upper_bound({ x, 0, 0, 0 });
				if (it != S.begin()) {
					it = prev(it);
					if (it -> r > x) {
						// 将 it 分裂开来
						int l = it -> l, r = it -> r, w = it -> who;
						int lv = yzh.query(l, x - 1), rv = it -> cnt - lv;
						S.erase(it);
						if (lv) S.insert({ l, x - 1, lv, w });
						if (rv) S.insert({ x + 1, r, rv, w });
						// 空了的我们不放到 set 里
					}
				}
				yzh.modify(x, 1);
				S.insert({ x, x, 1, k });
			};
			
			insert(R[i], bl[p[L[i]]]);
			insert(L[i], bl[p[L[i]]]);
		}
		
		Iter cur = S.lower_bound({ L[i], 0, 0, 0 });
		for (Iter it = next(cur); it != S.end() && it -> r < R[i]; it = S.erase(it)) {
			merge(it -> who, cur -> who);
			cur -> cnt += it -> cnt;
			cur -> r = it -> r;
		}
		// 统统合并起来
		
		if (toleft[i]) {
			static auto erase = [] (int x) -> void {
				Iter it = prev(S.upper_bound({ x, 0, 0, 0 }));
				if (!--it -> cnt) S.erase(it);  // 空了的我们不放到 set 里
				yzh.modify(x, -1);
			};
			erase(L[i]), erase(R[i]);
		}
    }
    long long ans[2] = { 1, 0 };
    for (int i = 1; i <= n; ++i) {
        if (!toleft[i] && !vis[get(bl[i])]) {
			vis[get(bl[i])] = true;
			++ans[yzh.query(L[i]) & 1];
		}  // 表明是这个连通块第一次出现，将背景色块数加一
        if (!toleft[i]) { // 加边
            int cnt = yzh.query(L[i] + 1, R[i] - 1) + 1;  // 块数
            if (yzh.query(L[i]) & 1) {  // 最下面颜色是白色
                ans[0] += (cnt + 1) >> 1, ans[1] += cnt >> 1;
            } else {
                ans[1] += (cnt + 1) >> 1, ans[0] += cnt >> 1;
            }
            yzh.modify(L[i], 1), yzh.modify(R[i], 1);
        } else {  // 删边
            int cnt = yzh.query(L[i] + 1, R[i] - 1) + 1;
            if (cnt == 1) --ans[(yzh.query(L[i]) & 1) ^ 1];
            else if (yzh.query(L[i]) & 1) {
                ans[1] += (cnt - 2 + 1) >> 1, ans[0] += (cnt - 2) >> 1;
            } else {
                ans[0] += (cnt - 2 + 1) >> 1, ans[1] += (cnt - 2) >> 1;
            }
            yzh.modify(L[i], -1), yzh.modify(R[i], -1);
        }
    }
    if (T == 1) printf("%lld", ans[0] + ans[1]);
    else printf("%lld %lld", ans[0], ans[1]);
    return 0;
}

去掉注释、卡常后的代码，目前是正解里 rank1。

#include <cstdio>
#include <set>
using namespace std;
 
const int MAX = 1 << 25;
char buf[MAX], *inp = buf;
template <typename T>
inline void read(T &x) {
    x = 0; char ch = *inp++;
	for (; ch <  48; ch = *inp++);
    for (; ch >= 48; ch = *inp++) x = (x << 3) + (x << 1) + (ch ^ 48);
}
 
const int N = 100010;
 
int n, T;
int L[N << 1], R[N << 1];
int toleft[N << 1], bl[N << 1], p[N << 1];
 
struct node {
    mutable int l, r, cnt, who;
    inline friend bool operator < (const node& a, const node& b) {
        return a.l < b.l;
    }
};
 
set<node> S;
using Iter = decltype(S.begin());
 
struct Bit_Tree {
    int tree[N << 1];
    inline void modify(int p, int v) {
        for (int i = p; i <= n; i += i & -i) tree[i] += v;
    }
    inline int query(int p) {
        int res = 0;
        for (int i = p; i; i &= i - 1) res += tree[i];
        return res;
    }
    inline int query(int l, int r) {
		int res = 0;
		for (--l; r > l; r &= r - 1) res += tree[r];
		for (; l > r; l &= l - 1) res -= tree[l];
		return res;
    }
} yzh;
 
int fa[N];
bool vis[N];
int get(int x) { return fa[x] == x ? x : fa[x] = get(fa[x]); }
inline void merge(int a, int b) { fa[get(a)] = get(b); }
 
signed main() {
    fread(buf, 1, MAX, stdin), read(n), read(T);
    for (int i = 1, x1, y1, x2, y2; i <= n; ++i) {
        read(x1), read(y1), read(x2), read(y2);
        L[x1] = L[x2] = y1, R[x1] = R[x2] = y2;
        toleft[x2] = p[y1] = p[y2] = x1, bl[x1] = i, fa[i] = i;
    }
    n <<= 1;
    for (int i = 1; i <= n; ++i) {
		if (!toleft[i]) {
			static auto insert = [] (int x, int k) -> void {
				auto it = S.upper_bound({ x, 0, 0, 0 });
				if (it != S.begin()) {
					it = prev(it);
					if (it -> r > x) {
						int l = it -> l, r = it -> r, w = it -> who;
						int lv = yzh.query(l, x - 1), rv = it -> cnt - lv;
						S.erase(it);
						if (lv) S.insert({ l, x - 1, lv, w });
						if (rv) S.insert({ x + 1, r, rv, w });
					}
				}
				yzh.modify(x, 1);
				S.insert({ x, x, 1, k });
			};
			
			insert(R[i], bl[p[L[i]]]);
			insert(L[i], bl[p[L[i]]]);
		}
		
		Iter cur = S.lower_bound({ L[i], 0, 0, 0 });
		for (Iter it = next(cur); it != S.end() && it -> r < R[i]; it = S.erase(it)) {
			merge(it -> who, cur -> who);
			cur -> cnt += it -> cnt;
			cur -> r = it -> r;
		}
		
		if (toleft[i]) {
			static auto erase = [] (int x) -> void {
				Iter it = prev(S.upper_bound({ x, 0, 0, 0 }));
				if (!--it -> cnt) S.erase(it);
				yzh.modify(x, -1);
			};
			erase(L[i]), erase(R[i]);
		}
    }
    long long ans[2] = { 1, 0 };
    for (int i = 1; i <= n; ++i) {
        bool f = yzh.query(L[i]) & 1;
        int cnt = yzh.query(L[i] + 1, R[i] - 1) + 1;
        if (!toleft[i] && !vis[get(bl[i])])
            vis[get(bl[i])] = true, ++ans[f];
        if (!toleft[i]) {
            ans[!f] += (cnt + 1) >> 1, ans[f] += cnt >> 1;
            yzh.modify(L[i], 1), yzh.modify(R[i], 1);
        } else {
            if (cnt == 1) --ans[!f];
            else ans[f] += (cnt - 1) >> 1, ans[!f] += (cnt - 2) >> 1;
            yzh.modify(L[i], -1), yzh.modify(R[i], -1);
        }
    }
    if (T == 1) printf("%lld", ans[0] + ans[1]);
    else printf("%lld %lld", ans[0], ans[1]);
    return 0;
}

后记

比用欧拉公式，线段树加并查集的做法是不是好多了？

Updated at 2024.12.15：修复了预处理的错误，润色文章，优化可读性。