[BJOI2016] IP地址 题解

前言

来个不一样的做法，用到了 Trie 树和主席树，并且是可爱的在线算法。

题目链接：洛谷。

题目分析

对于一个查询 \(\texttt{ip}\)，只考虑所有前缀字符串规则。以时间建里横轴，匹配长度为纵轴，建出坐标系。易知坐标系中有 \(\Theta(n)\) 条线段。对于某一时刻 \(t\)，根据题意，生效的匹配就是越过 \(t\) 的纵坐标最大的那条线段对应的前缀。用样例画张图吧。

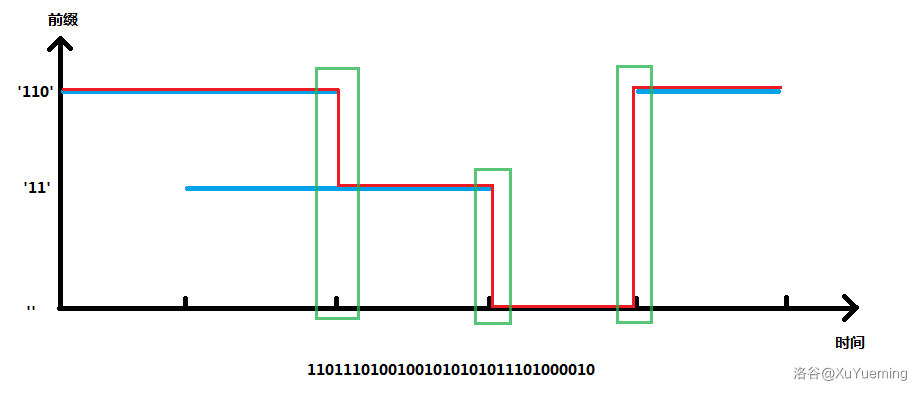
红色的线代表每一个时刻生效的匹配，绿色框内就是发生变化的时刻，分别是第 \(3\) 次操作后，第 \(4\) 次操作后，第 \(5\) 次操作后。

考虑使用 01-Trie 解决前缀。从根节点往下一直到匹配不上，每次将这个前缀出现的所有时段赋值为这个前缀的长度，就得到了红色的折线。最后查询 \([l, r]\) 内红色的线的纵坐标变化了多少次。

这个非常线段树啊，区间覆盖，合并信息也很容易，或者用珂朵莉树也可以。但是，直接这样做时间上是错误的，为什么？因为枚举这个前缀出现的所有时段是 \(\Theta(n)\) 的，可以轻松卡到 \(\Theta(nq \log n)\)。但是，原数据太水了，可以见这个帖子。

那么，做法呼之欲出了，预处理的时候把线段树可持久化就行了。但是要注意内存回收，注意结构体内存对齐，或者使用 #pragma pack(1)，空间有些紧的。

这个算法时间复杂度是 \(\Theta((n + q)(w + \log n))\)，空间复杂度是 \(\Theta(n (w + \log n))\)。

代码

略去了快读。

// #pragma GCC optimize(3)
// #pragma GCC optimize("Ofast", "inline", "-ffast-math")
// #pragma GCC target("avx", "sse2", "sse3", "sse4", "mmx")
#include <iostream>
#include <cstdio>
#define debug(a) cerr << "Line: " << __LINE__ << " " << #a << endl
#define print(a) cerr << #a << "=" << (a) << endl
#define file(a) freopen(#a".in", "r", stdin), freopen(#a".out", "w", stdout)
#define main Main(); signed main(){ return ios::sync_with_stdio(0), cin.tie(0), Main(); } signed Main
using namespace std;

#include <vector>
#include <bitset>

int n, q;

struct node{
	int son[2];
	vector<pair<int, int> > tim;
} tree[100010 * 20];
int tot;

void insert(char str[], int timer){
	int now = 0;
	for (int i = 0; str[i]; ++i){
		int t = str[i] - '0';
		if (!tree[now].son[t]) tree[now].son[t] = ++tot;
		now = tree[now].son[t];
	}
	tree[now].tim.push_back({timer, n});
}

void erase(char str[], int timer){
	int now = 0;
	for (int i = 0; str[i]; ++i){
		int t = str[i] - '0';
		now = tree[now].son[t];
	}
	int s = tree[now].tim.back().first;
	tree[now].tim.pop_back();
	tree[now].tim.push_back({s, timer});
}

struct President_Segment_Tree{
	struct node{
		int lson, rson;
		int val, lval, rval;
	};
	static node tree[200010 * 80];
	static int tot;
	static bitset<200010 * 80> tag;
	
	static inline void init(){
		tot = 0;
	}
	
	static inline int newNode(){
		int res = ++tot;
		tree[res] = {0, 0, 0, 0, 0};
		return res;
	}
	
	static inline int copyNode(int idx){
		int res = newNode();
		return tree[res] = tree[idx], tag[res] = tag[idx], res;
	}
	
	static inline void pushup(int idx){
		tree[idx].lval = tree[tree[idx].lson].lval;
		tree[idx].rval = tree[tree[idx].rson].rval;
		tree[idx].val = tree[tree[idx].lson].val + tree[tree[idx].rson].val + (tree[tree[idx].lson].rval != tree[tree[idx].rson].lval);
	}
	
	static inline void pushtag(int idx, int v){
		tag.set(idx);
		tree[idx].lval = tree[idx].rval = v;
		tree[idx].val = 0;
	}
	
	static inline void pushdown(int idx){
		if (!tag[idx]) return;
		pushtag(tree[idx].lson = copyNode(tree[idx].lson), tree[idx].lval);
		pushtag(tree[idx].rson = copyNode(tree[idx].rson), tree[idx].lval);
		tag.reset(idx);
	}
	
	int root[100010 * 20];
	
	void build(int &idx, int l, int r){
		idx = newNode();
		if (l == r) return;
		int mid = (l + r) >> 1;
		build(tree[idx].lson, l, mid);
		build(tree[idx].rson, mid + 1, r);
		pushup(idx);
	}
	
	void modify(int &idx, int trl, int trr, int l, int r, int val){
		if (trl > r || trr < l) return;
		idx = copyNode(idx);
		if (l <= trl && trr <= r) return pushtag(idx, val);
		pushdown(idx);
		int mid = (trl + trr) >> 1;
		modify(tree[idx].lson, trl, mid, l, r, val);
		modify(tree[idx].rson, mid + 1, trr, l, r, val);
		pushup(idx);
	}
	
	struct Q{ int val, lval, rval; };
	
	Q add(const Q & a, const Q & b){
		if (a.val == -1) return b;
		if (b.val == -1) return a;
		return {
			a.val + b.val + (a.rval != b.lval),
			a.lval, b.rval
		};
	}
	
	Q query(int idx, int trl, int trr, int l, int r){
		if (trl > r || trr < l) return {-1, 0, 0};
		if (l <= trl && trr <= r) return {tree[idx].val, tree[idx].lval, tree[idx].rval};
		pushdown(idx);
		int mid = (trl + trr) >> 1;
		return add(query(tree[idx].lson, trl, mid, l, r), query(tree[idx].rson, mid + 1, trr, l, r));
	}
} yzh;

President_Segment_Tree::node President_Segment_Tree::tree[200010 * 80];
int President_Segment_Tree::tot;
bitset<200010 * 80> President_Segment_Tree::tag;

void dfs(int now, int dpt = 0){
	for (const auto & [s, e] : tree[now].tim){
		yzh.modify(yzh.root[now], 1, n, s, e, dpt);
	}
	tree[now].tim.clear();
	tree[now].tim.shrink_to_fit();
	if (tree[now].son[0]){
		yzh.root[tree[now].son[0]] = yzh.root[now];
		dfs(tree[now].son[0], dpt + 1);
	}
	if (tree[now].son[1]){
		yzh.root[tree[now].son[1]] = yzh.root[now];
		dfs(tree[now].son[1], dpt + 1);
	}
}

signed main(){
	read(n, q);
	for (int i = 1; i <= n; ++i){
		static char op[5], str[50];
		read(op, str);
		if (*op == 'A') insert(str, i);
		else erase(str, i - 1);
	}
	dfs(0);
	for (int i = 1, l, r; i <= q; ++i){
		static char str[50];
		read(str, l, r);
		int now = 0;
		for (int j = 0; str[j]; ++j){
			int t = str[j] - '0';
			if (!tree[now].son[t]) break;
			now = tree[now].son[t];
		}
		write(yzh.query(yzh.root[now], 1, n, l, r).val, '\n');
	}
	return 0;
}