回文利器——回文自动机

前（che）言（dan）

回文树，也叫回文自动机，是2014年被西伯利亚民族发明的（找不到百度百科，从一篇博客里蒯过来的）

作为解决回文问题的大杀器，回文自动机功能强大，实现技巧充满智慧。——dalao

一个性质

一个长度为N的字符串最多有N个不同的回文子串。
为什么？

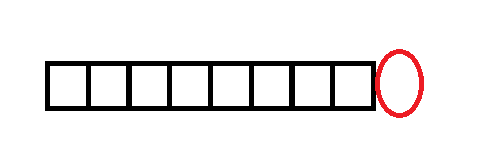
我们考虑加入一个字符能产生多少新的回文子串。

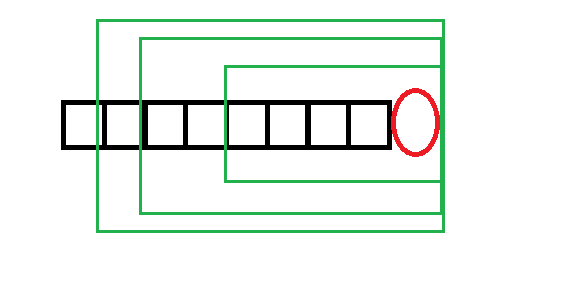
现在加入红圈位置的字符，假设绿框框起的都是回文串。然后我们发现一个神奇的事情

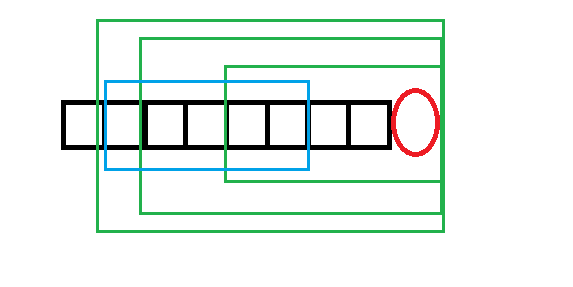
因为最大的绿框框起的串是回文的，所以蓝框框起的串和最小绿框框起的串是相反的。
然后又因为最小的绿框框起的是回文串（也就是说跟它相反的串就是它本身），所以蓝框框起的串和绿框框起的块是相同的。
也就是说这个最小绿框框起的串已经出现过了。不能提供一个新的本质不同回文子串。
所以，加入一个字符之后只有最长的一个回文串可能是一个新的本质不同的回文串。
所以可以证明：一个长度为N的字符串最多有N个不同的回文子串。
这个性质比较重要。

简述

回文自动机是一类可以接受字符串的所有回文子串的自动机。
状态数 \(O(n)\)
转移函数 \(O(n)\)
可以在线 \(O(n)\) 构造
回文自动机的一个节点代表一个回文子串。
因为刚刚的性质，所以回文自动机的状态数 \(O(n)\) 。

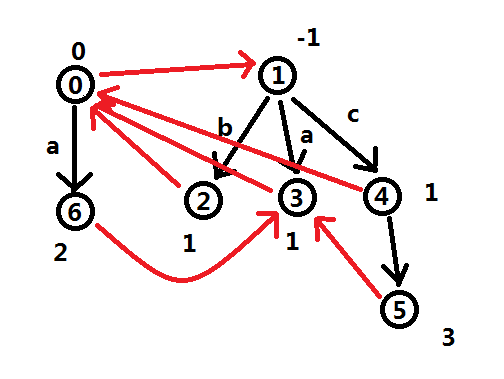
上图就是字符串bacaa的回文自动机。（节点上的数字是这个点的编号）
发现回文自动机有两棵树。一棵树代表长度为偶数的回文串，一棵树代表长度为奇数的回文串。
我们需要记录以下数值：
len[u] \(:\) \(u\) 节点代表回文串的长度。上图中在节点周围的黑色数字。
fa[u] \(:\) \(u\) 节点代表回文串的最长回文后缀代表的节点，上图中红色的边指向的就是自己的最长回文后缀。也就是说 \(fa[u]\) 其实就是上图的红边（ \(0\) 点到 \(1\) 点的红边没有上述意义，只是为了方便实现）一直跳 \(fa\) 就等于遍历 \(u\) 节点的所有回文后缀。
tran[u][c] \(:\) 转移函数，自动机必备的东西也就是上图中的黑色边，表示在 \(u\) 代表的回文串的两端加上字符 \(c\) 之后的回文串。
num[u] \(:\) 上图中并没有体现 \(num[u]\) ，代表 \(u\) 节点代表回文串的回文后缀个数。
L[i] \(:\) 并不是回文自动机上的东西，代表原字符串以 \(i\) 结尾的回文后缀长度。
size[u] \(:\) \(u\) 点代表的回文串的数量。

用途

维护了上面的这些东西。回文自动机可以求下面的东西：
1.求前缀字符串中的本质不同的回文串种类（就是节点数）
2.求每个本质不同回文串的个数（\(size\) 数组）
3.以下标i为结尾的回文串长度（\(L\)数组）

普通增量法构造

建议结合代码理解构造。
一开始只有两个点0,1。
所以

void init(){
        len[0]=0;fa[0]=1;len[1]=-1;fa[1]=0;
        tot=1;last=0;
        memset(trans[1],0,sizeof(trans[1]));
        memset(trans[0],0,sizeof(trans[0]));
}

这个应该不用解释。（PS：代码中tot为节点数，last为上次插入操作后的最长回文后缀长度，后缀自动机也有这个东西）

int new_node(int x){
    int now=++tot;
    memset(trans[tot],0,sizeof(trans[tot]));
    len[now]=x;
    return now;
}
void ins(int c,int n){
    int u=last;
    while(s[n-len[u]-1]!=s[n])u=fa[u];
    if(trans[u][c]==0){
        int now=new_node(len[u]+2);
        int v=fa[u];
        while(s[n-len[v]-1]!=s[n])v=fa[v];
        fa[now]=trans[v][c];
        trans[u][c]=now;
        num[now]=num[fa[now]]+1;
    }
    last=trans[u][c];size[last]++;
    L[n]=len[last];
}

增量法的主体函数—— \(ins\) 。
传两个参， \(c\) 代表当前插入的字符， \(n\) 代表当前插入字符在原串中的下标。
第一个 \(while\) 循环实际上是在寻找以当前位置为结尾的最长回文串。

while(s[n-len[u]-1]!=s[n])u=fa[u];

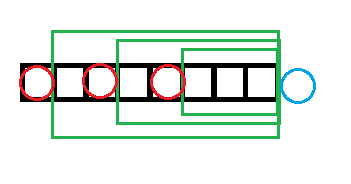
绿框框起的是回文串插入蓝圈位置的字符，从大到小枚举回文后缀看红圈位置的字符是否和蓝圈位置的字符相等。
然后判断以当前位置为结尾的回文串是否已经出现过。

if(trans[u][c]==0)

如果出现过直接维护一些值结束。

last=trans[u][c];size[last]++;
L[n]=len[last];

这应该能看得懂吧。。。
如果没有出现过，我们新建一个节点就行了。
但是我们还要维护一些量，比如新建节点的最长回文后缀。
所以我们接着进行第一个 \(while\) 差不多的工作——寻找以当前位置为结尾的第二长回文串后缀。来作为新建节点的最长回文后缀。
找到之后再维护一些量就行了。

int now=new_node(len[u]+2);
int v=fa[u];
while(s[n-len[v]-1]!=s[n])v=fa[v];
fa[now]=trans[v][c];
trans[u][c]=now;
num[now]=num[fa[now]]+1;

仔细研究我们发现，构造其实很精妙。
我们如果一直找不到以当前位置为结尾的回文串，在一直跳 \(fa\) 的时候最终会到达 \(1\) 节点。
我们看看 \(while\) 中的式子 \(s[n-len[u]-1]\) 当 \(u=1\) 的时候是多少？
因为 \(1\) 点的长度为 \(-1\)（\(len[1]=-1\)） ，发现 \(s[n-len[1]-1]\) 就是 \(s[n]\) 所以 \(while\) 最后一定会找到一个回文串也就是新加入的那一个字符。
假如第一个\(while\)找最长串就是这个字符了，你会发现你第二个 \(while\)找次长串 还是会找到这个字符，因为\(fa[1]=0,fa[0]=1\)。\(0\) 和 \(1\) 节点实际上是一个环。这样最后的维护还是正确的。
下面是完整的模板

struct PAM{
    int len[N],fa[N],size[N],num[N],tot,last,trans[N][27];
    void init(){
        len[0]=0;fa[0]=1;len[1]=-1;fa[1]=0;
        tot=1;last=0;
        memset(trans[1],0,sizeof(trans[1]));
        memset(trans[0],0,sizeof(trans[0]));
    }
    int new_node(int x){
        int now=++tot;
        memset(trans[tot],0,sizeof(trans[tot]));
        len[now]=x;
        return now;
    }
    void ins(int c,int n){
        int u=last;
        while(s[n-len[u]-1]!=s[n])u=fa[u];
        if(trans[u][c]==0){
            int now=new_node(len[u]+2);
            int v=fa[u];
            while(s[n-len[v]-1]!=s[n])v=fa[v];
            fa[now]=trans[v][c];
            trans[u][c]=now;
            num[now]=num[fa[now]]+1;
        }
        last=trans[u][c];size[last]++;
        L[n]=len[last];
    }
}pam;