Week10(线性DP)拿数问题、LIS&LCS

Week10(线性DP)拿数问题、LIS&LCS

 

 

 

 

 思路分析：

 　　LIS（longest increasing subsequence）最长上升子序列，意思是一个序列中递增的序列最大个数。首先要理解子串和子序列的概念。

     （1）字符子串指的是字符串中连续的n个字符，如abcdefg中，ab，cde，fg等都属于它的字串。

     （2）字符子序列指的是字符串中不一定连续但先后顺序一致的n个字符，即可以去掉字符串中的部分字符，但不可改变其前后顺序。如abcdefg中，acdg，bdf属于它的子序列，而bac，dbfg则不是，因为它们与字符串的字符顺序不一致。

　　求LIS是DP一个基本的运用，原理就是使用一个数组d[i]，表示以第i个数为结尾的最长子序列个数，求出每一个d[i]我们就可以求出答案了。而求d[i]

的状态转移方程是max(d[i],d[j]+1)，j<i .

　　LCS(longest common subsequence)最长公共子序列，是指一个两个序列的公共子序列S，是满足要求的子序列中最长的，我们叫S为最长公共子序列。求LCS也是动态规划（DP）一个基本的应用。首先我们定义d[i][j]，表示第一个序列前i个元素和第二个序列前j个元素的最长公共子序列的长度。d[n][m]就是我们所求的最终答案，而状态转移方程则为

 

 　　上述两个问题知道思路了代码就很好写了。

以下为代码：

 

#include <iostream>
#include <cstdlib>
#include <algorithm>
#include <string.h>

using namespace std;


int a[5010];
int b[5010];
int fa[5010];
int fb[5010][5010];

int n,m,ans=0;
int ans2=0;


int main(){
    
    cin>>n>>m;
    for(int i=0; i<n; i++) {
        cin>>a[i];
        fa[i] = 1;
    }
    for(int i=0; i<n; i++)
        for(int j=0; j<i; j++)
            if(a[j]<a[i])
                fa[i]=max(fa[i],fa[j]+1);
    for(int i=0; i<n; i++) 
        ans = max(ans, fa[i]);
    
    
    for(int i=0 ;i<m; i++){
        cin>>b[i];
    }
    
   memset(fb,0,sizeof(fb));
   
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            if(a[i-1]==b[j-1]) {
                fb[i][j]=fb[i-1][j-1]+1;    
            }else {
                fb[i][j]=max(fb[i-1][j],fb[i][j-1]);
            }
        }
    
    ans2=fb[n][m];
    
    cout<<ans<<" "<<ans2<<endl;
    return 0;
}

 

 

 

 

 

 

 思路分析：

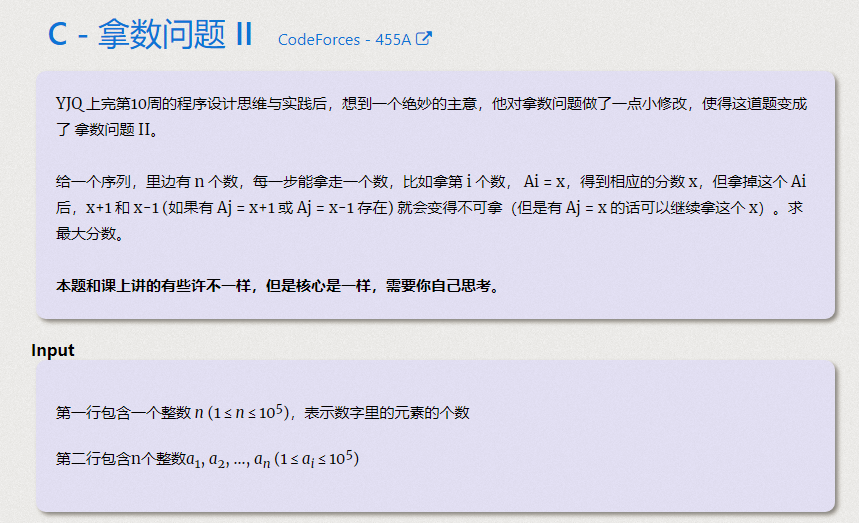
 　　对于课上讲的一般拿数问题，我们已经知道了它的动态表示和动态转移方程，但是这道题要求的不是相邻的不能拿，而是x+1和x-1不能拿。我们可以转化问题，将原来的序列排序，并记录每个数据出现的次数，并将这个数列填充成连续的，但是不记录填充的次数，这样，不能拿的数就必然相邻了，就可以成功将此问题转化成我们一般的拿数问题了。

 

以下为代码：

 

#include<iostream>
#include<algorithm>

#define LL long long 

using namespace std;

LL n;
LL ans;
LL a[100005];
LL dp[100005];
LL cont[100005]={0};

int main(){
    cin>>n;
    
    for(LL i=0;i<n;i++){
        cin>>a[i];
        cont[a[i]]++;
    }
    
    sort(a,a+n);
    
    for(LL i=a[0];i<=a[n-1];i++){
        dp[i]=max(dp[i-1],dp[i-2]+i*cont[i]);
        ans=max(ans,dp[i]);
    }
    cout<<ans<<endl;
    return 0;
}