Week16CSP模测M4
第四次CSP模测,本次测试是针对T1、T2和T4的模拟测试。T1、T4都拿满分了,但是T2全军覆没。总的来看,我好像这一段时间代码能力并没有进步了,反而前面有些知识点开始生疏了,例如T2的输出保留固定长度小数,我一时忘记了C++输入输出流中的 ...<<setiosflags(ios::fixed)<<... 和 ...<<setprecision(2)<<... 是怎么拼写的了,感觉类似的问题我还有不少。 再者我发现了我的读题能力是真的有待提高,首先是第一题就看了半天没看懂题目意思,就是题目描述里的最后一段话,真的是反复断句看了半天,结合案例连蒙带猜才勉强理解,因为给的样例太少了以知道最后交代码的时候我还不清楚到底有没有理解题意。然后就是T2直接看漏了题目信息,理解错了题意,不仅把一个很简单的题写复杂了,最后还是直接爆零。第三题是一个动态规划的题,属于这段时间做的很多的一类题了,一开始看到的时候毫无思路,甚至不知道用动态规划,详细题解见下文。
首先是T1,一开始被这道题的数据给唬住了,反复看样例、体面和数据范围,还是不很明白题意。其实就是判断一下一个数不同数位上总共有多少不同的数,任意一个数,最大值是10,我们一个个检查每一位就可以了, 总之,这道题很容易就AC了。


以下为代码:
#include<iostream> #include<string> #include<cstring> #include<cstdlib> using namespace std; bool b[10]; int main(){ int n,k; cin>>n>>k; int ans=0; long long temp; for(int i=0;i<n;i++){ memset(b,false,sizeof(b)); scanf("%lld",&temp); int cnt=0; while(cnt!=10&&temp>0){ int c=temp%10; temp=temp/10; if(b[c]==false){ b[c]=true; cnt++; } } if(cnt<k){ ans++; } } cout<<ans<<endl; }
第二题就很惨了,爆零,看了半天,原因竟然是看错了题目,题目要求选取的圆心在已知坐标点上,然而我看露了这句话,加上样例的圆心是以浮点数出现的,所以我想当然的以为圆心是计算出来的,不一定在坐标点上,然后爆零。
后来补题发现题目看错,其实圆心要求是输入坐标点,就是整数,(这里吐槽有误导性的样例)。给出的数据范围也很小,就直接枚举每一个点能覆盖的最小长度,然后最后取最小即可,注意一下长度相等的情况下优先考虑y坐标小的。

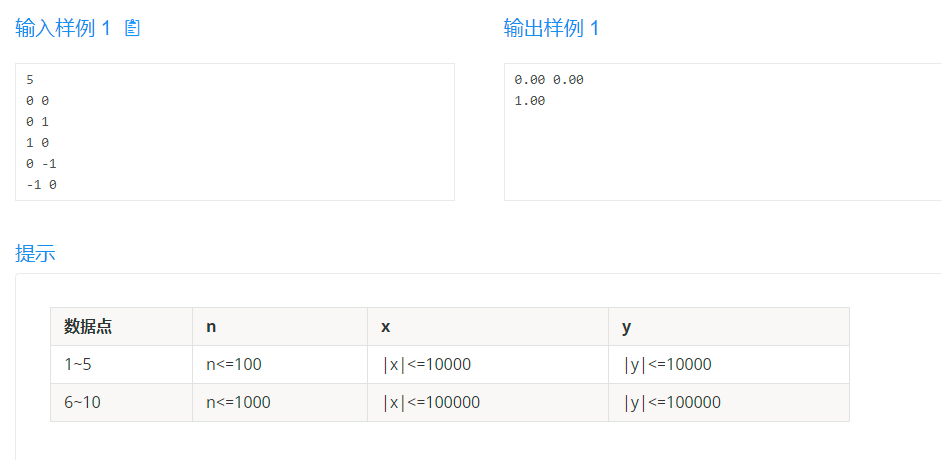
这道题本身真的不难啊,但是因为看错题而做错了真的感觉很可惜!
以下是补题阶段的AC代码:
#include<iostream> #include<cmath> #include<iomanip> #include<algorithm> #define ll long long using namespace std; const ll maxn=1e18; struct point{ int x; int y; }; bool cmp(point a,point b){ return a.y < b.y; } ll cal(point a,point b){ int t1=abs(a.x-b.x); int t2=abs(a.y-b.y); return pow(t1,2)+pow(t2,2); } point p[1010]; int main(){ int n; cin>>n; for(int i=0;i<n;i++){ int a,b; scanf("%d %d",&a,&b); p[i].x=a; p[i].y=b; } sort(p,p+n,cmp); // for(int i=0;i<n;i++){ // cout<<p[i].x<<" "<<p[i].y<<endl; // } point ans; ans.x=0;ans.y=0; ll r=0; ll ansd=maxn; for(int i=0;i<n;i++){ r=0; for(int j=0;j<n;j++){ ll temp=cal(p[i],p[j]); if(temp>r){ r=temp; } } // cout<<r<<endl; if(ansd>r){ ansd=r; ans.x=p[i].x; ans.y=p[i].y; } } int ta=ans.x; int tb=ans.y; cout<<ta<<".00"<<" "<<tb<<".00"<<endl; // cout<<setiosflags(ios::fixed); // cout<<setprecision(2)<<ta<<" "; // cout<<setprecision(2)<<tb<<endl; // cout<<setprecision(2)<<r<<endl; cout<<ansd<<".00"<<endl; return 0; }
第三题是一道动态规划的题。感觉还是很有水平的。一开始没有想到DP,一直在想能不能找到几种可能的前序或者后序序列,然后判断是否能成功构成二叉搜索树。但是后来发现要找到满足要求的前序序列太难了,如果采用枚举的方法,每次根据前序序列和中序序列,生产一棵树,并保证题目要求的时间复杂度为O(nlogn),但是总共有n!种不同的序列,即便可以稍微剪枝,但这也是感觉太大了行不通,最后想到这道题可能想考的是动态规划,想到状态转移方程就好做了。分析见下文。


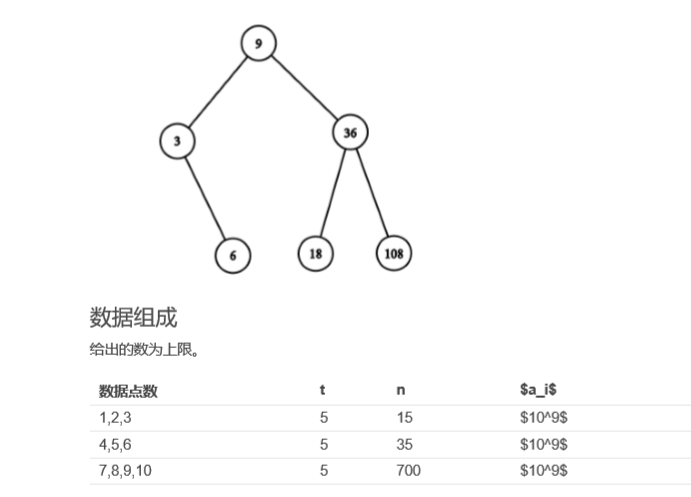
首先确定状态的表达,L[l][r] 表示r的左儿子可以是区间[l,r] ,即第l到r号元素,同理,R[l][r], 表示可以成为右孩子。对于每一种状态是否成立,我们要枚举每一种情况,即如果L[l][k]&R[k][r-1]&E[k][r] ,存在k,则可以成立L[l][r] ,对于R[l][r]也是同理,L[l+1][k]&R[k][r]&E[k][l]为真才成立。
一开始便初始化,然后再分别从长度为2开始(区间长度为1始终为真),进行DP。
最后只要判断是否存在根节点即可,即是否存在一个i使得L[1][i]&R[i][n]为真。
以下为代码:
#include<iostream> #include<string> #include<cstring> #include<cstdlib> using namespace std; int l,r,k; int a[710]; int L[710][710]; int R[710][710]; bool E[710][710]; int gcd(int a,int b){ return a%b==0?b:gcd(b,a%b); } int main(){ int t,n; scanf("%d",&t); for(int ii=0;ii<t;ii++){ memset(L,0,sizeof(L)); memset(R,0,sizeof(R)); memset(E,0,sizeof(E)); scanf("%d",&n); for(int i=1;i<=n;i++){ scanf("%d",&a[i]); } for(int i=1;i<=n;i++){ for(int j=1;j<=n;j++){ E[i][j]=(gcd(a[i],a[j])!=1)?1:0; } } for(int i=1;i<=n;i++){ L[i][i]=R[i][i]=1; } for(int len=1;len<=n;len++){ for(int i=len+1;i<=n;i++) for(int j=i-len;j<=i-1;j++) if(L[i-len][j]&&R[j][i-1]&&E[i][j]){ L[i-len][i]=true; break; } for(int i=1;i<=n-len;i++) for(int j=i+1;j<=i+len;j++) if(L[i+1][j]&&R[j][i+len]&&E[i][j]){ R[i][i+len]=true; break; } } bool flag=false; for(int i=1;i<=n;i++) if(L[1][i]&&R[i][n]){ flag=true; break; } if(flag){ cout<<"Yes"<<endl; }else{ cout<<"No"<<endl; } } }



