贪心题做题记录

贪心

贪心题合集，感觉不少都是结论题。 好吧其实不多

CF725F Family Photos

题意：有 \(n\) 对照片，Alice 和 Bob 轮流取，每一对照片只有取了第一张才能取第二张，如果连续两轮都不取就结束，每对照片对 Alice 和 Bod 的贡献分别是$ a_1,a_2,b_1,b_2$，两人都希望自己的总贡献-另一个人的总贡献尽量大，求最终的贡献差。

思路：对 \(a1+b1\) 和 \(a2+b2\) 的情况进行分类讨论。

如果 \(a_1+b_1<a_2+b_2\)：

1.\(a_1>b_2\)，那么有 \(a_1-b_2<a_2-b_1\)，\(b_1-a_2<b_2-a_1\)，因此两个人取第一张没有取第二张照片优，但是有 \(a_1-b_2>0\)，因此Alice一定会选择第一张，贡献为 \(a_1-b_2\)。

2.\(b_1>a_2\)，那么 Alice 取第一张两个人的差减小的比取第二张多，Alice 不会取第一张，而 Bob 取第一张会减小差距，所以一定会取第一张，此时 Alice 唯有取第二张，贡献为 \(a_2-b_1\)。

3.\(a_1\leqslant b_2\) 且 \(b_1\leqslant a_2\)，那么两个人先取的代价都为负，因此贡献为0。

如果 \(a_1+b_1\geqslant a_2+b_2\)，有 \(a_1-b_2\geqslant a_2-b_1\)，且 \(b_1-a_2\geqslant b_2-a_1\)，因此两人的策略都是取第一张。

这样一来，我们只用考虑唯一一种情况。为了统一加上 \(a_1\) 和减去 \(b_i\)，我们把照片权值变成 \(\frac{a_i+b_i}{2}\)，并在一开始就加上 \(\frac{a_i-b_i}{2}\)，那么这样每张照片对于 Alice 和 Bod 都是等价的，于是按价值排序后 Bob 取偶数位的价值即可。

trick：对于两个人轮流取，可以想办法把两个人的贡献统一，然后排序后间隔取。

CF1601D Difficult Mountain

题意：有 \(n\) 个人去爬山，山的高度是 \(d\)，每个人有两个属性 \(s,a\)，如果 \(s\geqslant d\) 那么它可以爬山，并把山高变成 \(\max(a,d)\)，求最多能让多少人登山。

思路：考虑对 \(\max(a,s)\) 和 \(s\) 进行双关键字排序，我们来证明一下这为什么是对的。

假设 \(s_i=\max(a_i,s_i)\)，那么对于 \(i\) 之前的人 \(j\)，一定有 \(\max(a_j,s_j)\leqslant s_i\)，\(i\) 一定可以爬；对于 \(i\) 之后的人 \(j\)，如果 \(\max(a_j,s_j)\) 都是 \(s_j\)，那么显然后面的人也可以爬，否则假如 \(a_k=\max(a_k,s_k)\)，再考虑 \(s_k\) 与 \(a_i\) 的关系，如果 \(s_k\geqslant a_i\)，这样没有影响，如果 \(s_k< a_i\)，那么 \(i\) 和 \(k\) 最多只能有一个人爬，而 \(a_k>a_i\)，所以让 \(i\) 爬一定更优，所以可以直接选择。

假设 \(a_i=\max(a_i,s_i)\)，那么如果 \(s_i<d\)，也就意味着 \(i\) 和之前的一个人只能有一个人爬，而 \(a_i>a_k\)，那么让 \(i\) 爬一定不优，于是直接不选即可。

复杂度 \(O(n\log n)\)。

trick：通过分讨求出两个元素之间的大小关系，然后就可以排序选取了。

CF875F Royal Questions

题意：有 \(n\) 个王子和 \(m\) 个公主。每个公主有两个喜欢的王子，编号分别为 \(a_i\),\(b_i\)，但一个王子只能娶一个公主（一个公主也只能嫁给一个王子）。每个公主有嫁妆价值为 \(w_i\)，求国王能够得到的嫁妆的最大值。

思路：考虑建边，边 \((u,v)\) 表示 \(u\) 把公主让给了 \(v\)，那么一个点的入度最多为 1，即形成了一个外向基环树森林。于是按 \(w_i\) 从大到小加边，用并查集维护连通性，并记录当前连通块是树还是基环树，如果两个点已经联通，那么如果原来是树，就可以选并变成基环树，否则只要不是两棵基环树就可以选择，如果两棵树合并就还是树，否则是基环树。

trick：对于选择最大的匹配，可以建图，转成在树或者基环树让边选择对应的点，然后贪心处理。

P6631 [ZJOI2020] 序列

题意：有长为 \(n\) 的序列 \(a\)，有 3 种操作，一是将 \([l,r]\) 中所有数减 1，二是将 \([l,r]\) 中下标为奇数的数减 1，三是将 \([l,r]\) 中下标为偶数的数减 1，你可以指定每次操作的类型和区间，求最少的操作次数让所有数都变成 0。

思路：把 \(l,l+2,l+4\) 这样的线称作从 \(l\) 开始的跳线，否则叫直线。首先考虑前两个位置，可以发现一定是从 \(1\) 开始 \(\min(a_1,a_2)\) 条直线和 \(a_1-\min(a_1,a_2)\) 条跳线，这样 \(a_1\) 就是 0 了，可以不管。

接着考虑第 2、3 个数。此时唯一的区别是可能有前面的线覆盖，因为如果能延用之前的线那么一定不劣。设前面的直线有 \(A\) 个，跳线有 \(B\) 个，那么如果 \(a_3>A+B\)，可以直接将 \(a_3\) 减去 \(A+B\)，否则就会有 \(K=A+B-a_3\) 条线无法延续下去。因为我们无法直接知道是保留直线还是跳线，我们可以先将 \(A,B\) 减去 \(K\)，然后在 3 处打上标记 \(K\) 表示可以使用 \(K\) 条线。可是如果 \(A,B\) 减成负数了怎么办？可以发现，如果 \(K>A\)，那么 \(B\) 至少得断掉 \(K-A\) 条，直接减去即可。

一直按这样推下去即可。

trick：递推顺次贪心。

P4577 [FJOI2018] 领导集团问题

题意：求树上LDS。

思路：可以类比序列上的LDS，每次找到第一个比 \(a_i\) 小的数，用 \(a_i\) 替换掉，唯一的问题是多个儿子进行合并的复杂度，于是用启发式合并就可以了。复杂度 \(O(n\log n)\)。

trick：类比传统模型，尝试套用一样的方法。

CF526G Spiders Evil Plan

题意：有一棵树，有边权，多次询问，每次给出 \(x,y\)，要求选出 \(y\) 条路径，使得形成一个包含 \(x\) 的联通块，求边权和的最大值。

思路：首先有结论，用 \(k\) 条路径就可以覆盖有 \(2k\) 个叶子的树。证明可以考虑先随意匹配再调整。回到原题上，就是要选不超过 \(2y\) 个叶子使得边权和最大。我们还可以发现，一定有一种最优解的方案使得直径的两端中至少有一端被选。于是我们以两个直径端点为根，在两棵树中分别查答案。

在一棵树中，因为已经钦定了根节点被选，那么我们就是要再选 \(2y-1\) 个叶子到根的链，同时让边权和最大。这启发我们用长链剖分，因为贪心地选取前 \(2y-1\) 长的链一定最优。

现在唯一的问题是如果 \(x\) 没有被选上怎么办。这时有两种情况，一种是我们放弃选择最后的第 \(2y-1\) 条链，然后选择 \(x\) 所在的链，另一种是先把 \(x\) 所在链选上，然后删去这条链向根延伸时碰到的第一个被选的点所在的链，然后删去这条链在这个点下面的部分即可。第二种情况可以直接树上倍增。复杂度\(O((n+q)\log n)\)。

trick：树上的贪心通常可以往长链、直径方面想。

P6831 [IOI2020]嘉年华奖券

题意：有 \(n\) 种颜色的奖券，每种 \(m\) 张，每张有价值 \(a[i][j]\)，有 \(k\) 轮，每轮第要从每种剩下的里面挑各挑一张，设这 \(n\) 张的中位数为 \(x\)，那么可以获得 \(\sum\limits_{i=1}^n|a_i-x|\) 的价值，求 \(k\) 轮总价值的最大值和方案。

思路：首先考虑，假如我们知道了我们总共用了哪些奖券，那么其中有 \(\frac{nk}{2}\) 个取正贡献，\(\frac{nk}{2}\) 个取负贡献，并且每一轮中取负贡献的比取正贡献的值小。这样就可以推出，一定存在一组最优解满足可以把这 \(nk\) 个数分成 \(k\) 组，使得每组中的 \(n\) 张奖券的颜色互不相同。

于是先要确定选哪些奖券。这一步可以直接贪心，先默认取负贡献，然后再贪心地把 \(\frac{nk}{2}\) 个变成正贡献即可。

接着就是如何构造方案。设一种颜色取正贡献的有 \(cnt_i\) 张，那么每一轮取 \(cnt_i\) 前 \(\frac{n}{2}\) 大的取正贡献，否则取负贡献，一直递归下去就可以了。

P3269 [JLOI2016] 字符串覆盖

题意：给定字符串 \(a\) 和若干子串，要求用子串覆盖一些匹配的位置，求覆盖集合的大小的最小、最大值。

思路：首先，用哈希求出每个串的所有出现位置。

先看最大值。可以考虑 \(n!\) 来枚举所有串起始位置的相对大小关系，然后 \(2^{n-1}\) 来判断两两是否重叠，再直接填就可以了。

再看最小值。首先，如果一个串是另一个串的子串，显然是把小串和大串重叠，于是可以不用考虑小串。于是可以状压 DP。设 \(f[i][S]\) 表示 \(S\) 中的字符串右端点最大的字符串右端点在 \(i\) 时覆盖的最小总长度，考虑枚举贴着右端点的串是 \(x\)，那么有转移

1.\(f[i][S]\leftarrow f[k][S/x]+len_x,(k<i-len_x)\)

2.\(f[i][S]\leftarrow f[k][S/x]+i-k,(i-len_x\leqslant k<i)\)

但是第二种转移如果超过了下界那么答案不会更优，于是可以把下界变成0，这样就相当于是前缀min，可以直接维护。

P4331 [BalticOI 2004] Sequence 数字序列

题意：给定一个整数序列 \(a_1, a_2, \cdots , a_n\)，求出一个递增序列 \(b_1 < b_2 < ··· < b_n\)，使得序列 \(a_i\) 和 \(b_i\) 的各项之差的绝对值之和 \(|a_1 - b_1| + |a_2 - b_2| + \cdots + |a_n - b_n|\) 最小。

思路：首先，如果严格递增，那么\(b_i=a_i\)；如果不增，那么就取中位数。

再考虑更一般的情况，很自然的想法就是把每一段不升的段取中位数，但是可能取完后不递增，这时需要继续合并，于是用可并堆来维护合并和求值。

trick：从特殊情况入手。

P4364 [九省联考 2018] IIIDX

题意：一棵树，要对树上的每个点标上给定的权值，满足每个点上的权值都 \(\le\) 子树内点的权值，并使这个棵树编号从小到大的权值字典序最大。

思路：情况分两种，一种是所有数都不相等，可以直接贪心放。

一种是所有数都相等，我们先考虑让本层答案最大，因此需要先为每个子树预留一定的数。具体的，我们把权值从小到大排序，然后用线段树维护每个权值左边还能取的权值个数，这样我们确定一个点 \(x\) 的权值时，需要给子树在 \(x\) 左边预留权值，就相当于是把后缀减 \(siz[x]\)。取一个点的权值时，就在线段树上二分出最大的权值满足其右边所有权值还能取的数量 \(\geqslant siz[y]\)。

P7417 [USACO21FEB] Minimizing Edges P

题意：构造新图G'，边数最短的满足若在 G 上 \(n\) 点能从点 1 走 \(k\) 步到达，则 G' 上也应同样满足；且不存在点 \(n\)，G' 上能走 \(k\) 步到达而在 G 上不能。

思路：想到了第一步，就是处理出到 \(i\) 的奇、偶最短路，这样就与原图无关了。

然后把这两个数当做一个二元组 \((x,y),x<y\)，那么有两种方式，一种是从 \((x-1,y-1)\) 连一条边，第二种是从 \((x-1,y+1)\) 或 \((x+1,y-1)\) 连过来。

于是可以贪心。按 \(x+y\) 为第一维，\(x\) 为第二维考虑，这样我们考虑 \((x,y)\) 时，如果 \((x-1,y+1)\) 没有传过来，就用第一种方式，因此有一部分 \((x,y)\) 用于满足需求，还有的向 \((x+1,y-1)\) 传，一直到 \(x+1=y\) 停止。这样传到边界是可以用 \(\dfrac{1}{2}\) 的代价消掉，就可以将原来的 2 降到 1.5。

trick：按一定方式给元素定序可以更好处理问题。

[AGC004F] Namori

题意：给定一个 \(N\) 个点，\(M\) 条边的图，没有自环，没有重边。其中 \(N-1\le M\le N\)，每个点初始是白色。每次操作可以处理一条边，其两个点如果颜色相同则都变成相反的颜色（黑变白，白变黑）。询问能否将每个点都变为黑色。如果能，输出最少的操作数；如果不能，输出 \(-1\)。

思路：转化成把树黑白染色，然后每次操作相当于对调黑白点的颜色，于是有解的条件是染色后黑白点数目相等。

先考虑树，那么一个点的权值就是子树里黑白点的个数之差，相当于考虑经过当前点连向父节点的边的数量，答案就是所有点的总和。

再考虑偶环基环树。考虑减掉一条边对答案的影响，相当于是这条边右边的点权值减 \(x\)，左边加 \(x\)，这样就可以转成数轴上找一个点到其他点距离和最小的点的问题，可以直接找中位数。

剩下的就是奇环基环树。此时不再是二分图，一定有一条边连接的两点的颜色相同，那么对这条边操作相当于是黑点数量 +2 或 -2，那么只需让答案增加黑点个数的一半即可。

trick：只有两种颜色的染色，可以考虑二分图的角度。

[AGC010E] Rearranging

题意：有一个 \(n\) 个数组成的序列 \(a_i\)。

高桥君会把整个序列任意排列，然后青木君可以进行任意次操作，每次选择两个相邻的互质的数交换位置。

高桥君希望最终序列的字典序尽量小，而青木君希望字典序尽量大。求最终序列。

思路：神仙题，那种想半天没有头绪结果一看题解发现好简单的题。

首先考虑如果先手已经操作完了后手应该怎么操作。发现一个性质，如果两个数不互质，那么显然这两个数的相对位置就不会变，于是可以把这样的位置间连边，字典序最大的一组拓扑序就是答案。

再考虑先手的策略。先手要做的就是对每一个连通块定向，使得最大拓扑序最小，可以直接贪心地每个点从小到大连边。这样可以保证每个连通块都是最优的。

trick：交换相邻 \(\rightarrow\) 考虑相对关系。

CF1073F Choosing Two Paths

题意：给出一个无根树，请从中选取 2 条链，其中任何一条链的端点不能被另一条链包含，请求出符合题意的链对，并使这两条链的公共的点的部分最长，在此基础上链长的和最大。

思路：首先，链交肯定是最长的一条链满足端点度数大于 2，可以直接按类似求直径的方法通过两遍 dfs 来解决。

最后求链长就直接求最长、次长链就行了。

trick：树上的贪心可以尝试直径和长链。

CF1214F Employment

题意：有一个长度为 \(m\) 的环形铁路，在铁路的某些点上有一些人或一些办公室，现在要求给每个人配一个办公室，让所有人的上班路程最短。人和办公室的数量都是 \(n\)。

思路：鉴定为无思维难度，但实现上不好写，细节多。

有稍微好写点的方法。先把 \(a,b\) 序列复制一份，于是变成了 \(\min\limits_{x=0}^{2n}\sum\limits_{i=1}^n|a_i-b_{i+x}|\)

考虑这个式子的差分，发现 \(a_i\) 对差分的贡献是 \(-2a_i[b_{i+x-1}<a_i<b_{i+x}]\)，\(b_i\) 同理，这样比较好写。

trick：有相减的贡献可以考虑差分。

CF1452F Divide Powers

题意：有一个只含有 2 的整数次幂的可重集合，你可以将 \(2^l\) 切成 2 个 \(2^{l-1}\)，带修，求最少的操作次数使得至少有 \(k\) 个元素不超过 \(2^x\)。

思路：思路还好理解，但是不太会实现。

我们发现有3种操作：

1.把 \(2^i\) 通过 \(2^i-1\) 次操作变成 \(2^i-1\) 个 1（\(i\in [0,x]\)）

2.把 \(2^i\) 通过 \(2^{i-x}-1\) 次操作变成 \(2^{i-x}\) 个 \(2^x\)（\(i\in(x,n]\)）

3.把 \(2^i\) 变成不超过 \(2^{i-x}\) 个不超过 \(2^{x}\) 的数（\(i\in (x,n]\)）

发现第二种的贡献比例大于 1，于是肯定先做二操作。如果还差超过 \(2^{i-x}\) 个，那么就用 3 操作，最后再用 1 操作。

复杂度 \(O(qn)\)。

CF1469F Power Sockets

题意：初始给出 \(n\) 条长度分别为 \(l_1,l_2,\dots,l_n\) 的链，以及一棵只有一个根节点的树，所有点初始都为白色。

• 每次操作可以用一条边将一条链中的一个点 \(u\) 和树上某个白点 \(v\) 连接起来，\(u,v\) 都变黑。一条链至多操作一次，也可以不操作。
• 操作完后树的权值为根节点到第 \(k\) 近的白点的距离。问操作方案所得树中最小的权值。

思路：想到了每次肯定是把链的中点和深度最浅的白点连起来，而且链肯定是从小往大或从大往小加。

没想到的是可以直接维护 \(f_i\) 表示第 \(i\) 层还剩的白点数，然后每次的操作就是区间加和查询最小的非0位置，可以直接线段树上二分。

也有更优雅的做法，即维护差分，然后双指针。

CF1493E Enormous XOR

题意：定义 \(g(x,y)=x\oplus\ (x+1)\oplus\dots\oplus\ (y-1)\oplus\ y\) ，\(f(l,r)\) 为所有满足 \(l\leq x\leq y\leq r\) 的 \(g(x,y)\) 的最大值，给定两个 \(n\) 位二进制数 \(l\) 和 \(r\) ，求 \(f(l,r)\)。

思路：真·诈骗题

首先，如果 \(l,r\) 的最高位不相等，那么答案就是全1，由\(10000\cdots\) 和 \(011111\cdots\)异或得来。

其次，如果 \(l,r\) 的最高位都是 0，又因为当 \(x\) 为偶数时，\(x\oplus (x+1)=1\)，因此最终答案一定是由 0 或 1 或 2 个数或 3 个数异或而来，而如果是两个数异或而来那么最高位是0，因此只能是1个数或 3 个数，这样最大的就是 \(r\)，这时只用判能否让答案为 \(r|1\) 就行了。

trick：从特殊情况入手。

CF1637H Minimize Inversions Number

题意：给定一个 \(1\sim n\) 的排列 \(p\)。 你可以进行下列操作正好一次：- 选定 \(p\) 的一个长度为 \(k\) 的子序列，并将其按照相同的顺序移动到 \(p\) 的最前面。对于 \(k=0,1,\cdots,n\)，分别求出 \(p\) 在操作后的最小逆序对数。

思路：贪心+推式子题。

首先，把一个数移到开头对逆序对的贡献是 \(-(\sum\limits_{j=1}^{i-1}[p_j>p_i]-\sum\limits_{j=1}^{i-1}[p_j<p_i])\)，记为 \(d_i\)，那么假设把 \({i_1,i_2\cdots i_k}\) 移到最前面的贡献就是 \(inv(p_1\sim p_n)-(\sum\limits_{j=1}^kd_j+((\binom{k}{2}-inv(q_{1\sim k}))-inv(q_{1\sim k})))\)，即最大化 \(\sum d-2inv(q_{1\sim k})\)。

我们发现这样还是不好处理，于是考虑找一些性质。有一个结论，如果 \(i<j,p_i>p_j\)，那么如果 \(i\) 在子序列里，那么 \(j\) 也在子序列里肯定不劣。于是式子的第二项可以写成 \(\sum\limits_{j=1}^k\sum\limits_{l=i_j+1}^n[p_l<p_{i_j}]\)，设 \(c_i=d_i-\sum\limits_{j=i+1}^n[p_j>p_i]\)，这样答案就是 \(\sum c\)，直接排序后从小到大取就行了。

trick：通过分析性质简化贡献形式。

P6072 『MdOI R1』Path

题意：一棵树，有边权，要选择两条简单路径，满足没有重合的点，且边权异或和之和最大。

思路：标算 \(O(n\sqrt{n}\log w)\)，但是被 \(O(n\log w)\) 的贪心碾了。

首先，可以通过设置点权来把边权和转成点权和，然后用01trie 取出异或和最大的路径，这时答案分两种情况：

1.这条路径是答案之一，那么就把剩下的子树每个求一遍答案然后取最大值就行，复杂度 \(O(n\log w)\)。

2.这条路径上的一部分边被分割开，那么就相当于是以其中一个端点为根，断开链上的一条边，可以两遍求出每个子树和剩余部分的答案，然后加起来即可，复杂度 \(O(n\log w)\)。

于是总复杂度就是 \(O(n\log w)\)。

trick：树上对路径的操作通常可以差分转成单点操作。

CF1027F Session in BSU

题意：有 n 场考试，每场考试你有两个时间点 \(a_i,b_i\) 可以考，你可以选择一天去考，然后经过你的合理安排，你需要将这n场考试都考掉，并且求出最少要多少太天才能考完，即考完的最后一天，如果无法做到将所有考试考完，那么就输出-1

思路：简单题。

考虑对每一对限制 \((a_i,b_i)\)，连双向边 \((a_i,b_i)\)，这样对于每一个连通块：

如果边数大于点数，那么即无解；

如果是一颗树，那么就有一个点可以不用选，因为要求尽量早，所以就选择最大的点不选；

如果是基环树，那么显然每个点都会被选上。

trick：对于匹配，可以建图，在树或者基环树上处理。

CF1329C Drazil Likes Heap

思路：想了半天怎么把这个操作简化，结果你告诉我可以直接贪？

因为是大根堆，所以每次如果能 \(f(1)\) 肯定 \(f(1)\) 最优，否则就尝试 \(a_2,a_3\) 中较大的那个，然后继续下去。这个过程可以用堆来维护，每次如果堆顶可以操作就操作，否则就弹出，然后加入左右孩子。

这就做完了？

trick：裸的贪心有时候不是那么好想。

CF1601E Phys Ed Online

思路：根据贪心，答案是 \([l,l][l,l+k],[l,l+2k]...\) 的最小值之和。我们设 \(f_l\) 表示 \(\sum\limits_i\min(l,l+ik)\)，那么设区间最小值所在位置为 \(p\)，那么有 \(ans=f_l-f_p+a_p(r-p+1)\)。关键在与 \(f\) 的求法，我们找到每个数后面第一个比他小的位置 \(nxt_i\)，那么 \(f_i=f_{nxt_i}+(nxt_i-i)a_i\)，这样就简单了。

CF1693E Outermost Maximums

题意：有一个长度为 \(n+2\) 的序列 \(a\)，其中 \(a_0=a_{n+1}=0\)，其余元素均给定。
你可以进行下面两种操作任意次：

1. 设 \(x\) 表示序列 \(a\) 最靠左的最大值的位置，则令 \(a_x\leftarrow \max_{i=0}^{x-1}a_i\)。
2. 设 \(y\) 表示序列 \(a\) 最靠右的最大值的位置，则令 \(a_y\leftarrow \max_{i=y+1}^{n+1}a_i\)。

你需要求出使序列 \(a\) 的所有元素均变成 \(0\) 所需的最少的操作总次数。

思路：考场上想到了错贪（其实就是正贪）。

贪心的思路就是对于每一轮，如果操作一的变成的数更小就进行操作一，否则就进行操作二。

考虑怎么维护这个过程。我们可以看成，从大到小考虑每个数，我们先把当前值的所有位置标记成 "未确定要赋成前缀最大值还是后缀最大值"，那么访问到一个更小的值的时候，如果这个值最左的出现位置位于一个未确定的位置的左侧，那么这个未确定位置肯定是赋成后缀最大值才更小，同理，如果这个值的最右位置位于一个未确定的位置的右侧，那么这个未确定的位置肯定赋成前缀最大值更小，于是我们可以维护这3种情况的分界点，分界点左侧是要赋成前缀最大值，中间是未确定，右侧要赋成后缀最大值。

实现上，用一个树状数组来维护每个位置是否有值，然后每加入一个值就分类讨论一下即可。

QOJ# 5378. 匹配问题

题意：数轴上有 \(n\) 个黑点，坐标为 \(a_i\)；\(n\) 个白点，坐标为 \(b_i\)。同时你有两个参数 \(la\) 和 \(lb\)，满足 \(n\ge 2\) 且 \(1\le lb<la\)。注意同一个位置可能有多个点。你需要找到一个 \(0\) 到 \(n−1\) 的排列 \(p\)，满足对于所有 \(i\)，有 \(a[i]\le b[p[i]]\le a[i]+la\)。你需要最大化满足 \(b[p[i]]\le a[i]+lb\) 的下标 \(i\) 的个数。数据保证存在一个合法的排列。

思路：神仙贪心题。

考虑按A从右到左匹配，考虑当前最右的没有匹配的位置 \(x\) 和最右边的满足 \(b[y]+lb\leqslant a[i]+la\) 的 \(y\)，那么考虑什么时候选择匹配 \(x\)。考虑 \(a\) 的右端点和 \(b\) 的左端点构成的序列，如果存在 \(z>y\) 使得 \(z\) 右边的右端点和左端点数量相等，那么选择了 \(y\) 就会使得剩下的无法匹配，这时就只能匹配 \(x\)，否则就匹配 \(y\)。

用线段树维护这个过程就是 \(O(n\log n)\)。

P6287 [COCI2016-2017#1] Mag

题意：一棵树有点权，一条路径的贡献是路径上点的点权之积除以路径上点数，求贡献最小的路径。

思路：推出了一些小结论，比如保留全 1 链，而且最多有一个非 1 权值，不过没发现只有 2 才有用。

结论：

1. 如果不存在魔力值为 1 的节点，答案为魔力值最小的节点的魔力值。
2. 如果存在魔力值为 1 的节点，答案只有可能是以下两种：全 1 链和两条长度相等的全 1 链中间由魔力值为 2 的点连接。

而我们可以不用管 2 的位置，因为这样不会影响答案，那么对每个点维护最长的 1 链和 2 链即可。

trick：对于贡献是乘积，可以多考虑 1 的作用。

[AGC032E] Modulo Pairing

题意：令 \(M\) 为一正整数。给出 \(2 N\) 个整数 \(a_1, a_2, \ldots , a_{2N}\)，满足 \(0 \le a_i < M\)。你需要把这 \(2 N\) 个整数分成 \(N\) 对，每一对 \((x, y)\) 的权值为 \((x + y) \bmod M\)。令一种分配方案的权值为每一对的权值的最大值，请问权值最小的分配方案的权值为多少？

思路：好题。

一开始的思路就是错的。。。

正解很神。

首先，把所有数从小到大排序后，我们的选择肯定形如：

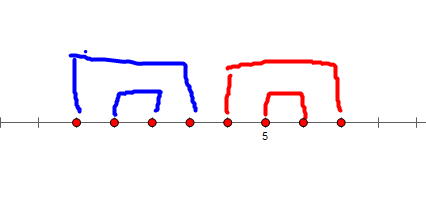
蓝线表示选择两个和 \(<mod\) 的数，红线表示选择两个和 \(\ge mod\) 的数。

证明：

显然，确定了哪些点连蓝、红线之后，他们之间一定是大的连小的，那么只用证明以下的情况不优：

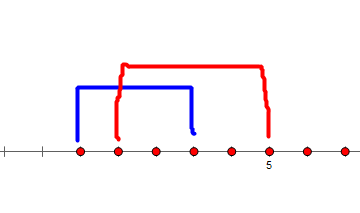
设点为 \(a,b,c,d\)，我们有 \(a+c<mod,b+d\ge mod\)，答案为 \(\max(a+c,b+d-mod)\)，那么调整后答案为 \(\max(a+b,c+d-mod)\)，而因为 \(c+d-mod<c\le a+c\)，于是调整后一定不劣，这样就能证明了。

于是我们二分蓝、红线的分界点即可。

trick：对于求匹配让 max 最小，通常是小的和大的进行匹配

[AGC053D] Everyone is a winner

题意：有一场 \(n\) 个参赛者、\(n\) 道题的比赛。参赛者被编号为 \(1\) 至 \(n\)。我们知道每一名参赛者解决每一道题目需要的时间，其只可能是 \(1/2/3\) 分钟。在这 \(n\) 道题目中，有 \(A_i\) 道题目需要参赛者 \(i\) 花费 \(1\) 分钟解决，有 \(B_i\) 道题目需要参赛者 \(i\) 花费 \(2\) 分钟解决，有 \(C_i\) 道题目需要参赛者 \(i\) 花费 \(3\) 分钟解决。

假设每名参赛者都能够自由决定做题顺序，请确定如下的条件是否能够对于所有参赛者 \(1\le i,j\le n\) 都成立：

• 令 \(S\) 为参赛者 \(i\) 完成前 \(i\) 道题目的时间，\(T\) 为参赛者 \(j\) 完成前 \(i\) 道题目的时间。条件即为 \(S\le T\)。

具体的说，在忽略切换题目的时间的情况下，需要确定是否对于每个参赛者 \(i\)，其为所有人中第一个（可能为并列）完成前 \(i\) 道题目的人。

思路：又是一道不会证明的题。

对于第 \(i\) 个人，如果我们知道了前 \(i\) 题是什么题，那么前 \(i\) 题和后 \(n-i\) 题肯定都是倒序来的，于是考虑维护 \(T_i\) 表示对第 \(i\) 个人前 \(i\) 道题的限制，一开始就是每个人都倒序。

我们倒序考虑每个人，此时就是对于第 \(i\) 个人，要在满足时间不超过 \(T_i\) 的情况下最大，且最大化耗时为 1 的题目数量。

然后就不知道为什么可以证明不用考虑一个人对后面的人的贡献。

然后发现每个人都是一个斜率不超过 3 的折线，直接维护 3 种斜率的直线即可。

设 \(x,y,z\) 为 3 种耗时的题目的数量，那么有 \(x+y+z=i,x+2y+3z=t\)，那么 \(y=3i-2x-t,z=t+x-2i\)，每次更新时暴力从 \(T_i\) 开始枚举复杂度就是 \(O(n)\) 的。

CF360E Levko and Game

题意：你和你的朋友在一张有 \(n\)（\(n\le 10^4\)）个点， \(m+k\)（\(m \le 10^4\)，\(k\le 100\)）条边的带权有向图上玩一个游戏。一开始你们分别处在 \(S_1\) 和 \(S_2\) 上，你们需要到达 \(T\)。你可以将给定的 \(k\)(\(\le 100\)) 条边的权值修改为 \([L,R]\) 中任何数。在开局时,每条边的权值都在 \([L,R]\) 中。问你是否能先到达\(T\)，如果不能，能否达成平局。

思路：可能算小清新贪心题？（总是想不出来贪心题）。

每条边被改后显然是 \(l,r\) 中的一个。

首先考虑怎么让 \(s_1\) 赢。

对于一条边，如果 \(dis(s_1,t)\ge dis(s_2,t)\)，那么 \(s_1\) 肯定不会走，于是改成 \(r\) 可以让 \(s_2\) 走得更远；如果 \(dis(s_1,t)<dis(s_2,t)\)，那么这时 \(s_2\) 不会走这条路，那么改成 \(l\) 显然会让 \(s_1\) 更优。

这样就可以判断 \(s_1\) 能不能赢。

接着就是考虑能不能平。

如果 \(dis(s_1,t)>dis(s_2,t)\)，那么 \(s_1\) 肯定不会走，于是改成 \(r\) 可以让 \(s_2\) 走得更远。

如果 \(dis(s_1,t)\le dis(s_2,t)\)，那么走这条路会平局或者 \(s_1\) 赢，于是 \(s_2\) 不会走，改成 \(l\) 肯定更优。

可以在 \(\text{dij}\) 的过程中来更新边权，可以做到 \(O(m\log n)\)。

trick：对于取值有上下界，通常用到的只有上界、下界两个取值。

P2501 [HAOI2006] 数字序列

题意：求把一个序列变成严格上升的序列需要改变的最少元素数量和每个数改变量的最小值。

思路：感觉基于最长上升子序列衍生出了很多有意思的题。

首先，通过经典的 trick，令 \(a_i\rightarrow a_i-i\) 就可以把严格转成不严格，那么第一问就是最长不下降子序列长度。

然后就是第二问。

有一个贪心结论：对于区间 \([l,r]\)，存在一个分界点 \(k\) 使得 \(a_i=a_l(i\le k),a_j=a_r(j>k)\)。

对于点 \(i\)，设其为最长不下降子序列的末尾时上一个是 \(pre_i\)，那么对于 \((pre_i,i)\) 中的 \(j\)，有 \(a_j<a_{pre_i}\) 或 \(a_j>a_i\)，那么对于其中的一个区间，根据两类位置的数量可以知道可以与某一边相等，然后就可以调整至就结论中的形式。

因为数据随机，所以复杂度大概是 \(O(n\log n)\)。

trick：对于取值有上下界，通常用到的只有上界、下界两个取值

P3564 [POI2014] BAR-Salad Bar

题意：有一个长度为 \(n\) 的字符串，每一位只会是 \(p\) 或 $j 。求一个最长子串，使得不管是从左往右还是从右往左取，都保证每时每刻已取出的 \(p\) 的个数不小于 \(j\) 的个数。

思路：有一堆做法。

这里记一个优于 \(O(n)\) 的做法。

首先，满足条件的子串首尾肯定都是 \(p\)，于是可以去除前导 \(j\)，然后维护前后缀 \(p,j\) 的数量，当后缀 \(p,j\) 数量相同时就清零，为了防止后缀对前缀的影响。

P3584 [POI2015] LAS

题意：有 \(n\) 个人围成一圈，每个人的左边和右边都有一个食物，每个食物都有不同的热量，每个人可以吃掉他左边或者右边的食物，假如有 \(2\) 个人同时选择了一个食物，那么两个人会同时吃掉这个食物并平分这个食物的热量，否则自己一个人独自吃掉这个食物，现在需要每一个人吃到的热量是位于自己左边食物的热量和右边食物的热量的最大值，你需要给出每个人吃食物的方案。若无解，则输出 NIE。

思路：好像可以直接贪心。

首先把必须选某一边的处理掉，可以用队列维护。

剩下的直接选择两边较大的那个即可。

P4809 [CCC2018] 最大战略储备

思路：抽象题。

直接把所有边排序后从小到大选择，每条边被选择的次数就是当前另一维还剩多少。

trick：如果是常见模型的拓展可以从模型的处理方法来拓展。

P2519 [HAOI2011]problem a

题意：一次考试共有 \(n\) 个人参加，可能出现多个人成绩相同的情况。第 \(i\) 个人说：“有 \(a_i\) 个人成绩比我高,\(b_i\) 个人成绩比我低。”请求出最少有几个人没有说真话。

思路：首先定义一个人的排名是严格高于他的人数加1，然后就可以把每个限制改成：“我是第 \(a_i+1\) 名，算上自己共有 \(n-a_i-b_i\) 个人与我同分”，然后变成区间 \([a_i+1,n-b_i]\) 表示与第 \(i\) 个人分数相同的区间，并把这个区间的权值定义为区间长度与所有 \(a_j=a_i+1，j=n-b_i\) 的 \(j\) 的个数的较小值。然后我们就把问题转化成了要选出若干不交的区间，最大化权值和。

我们发现，对 \(f_i\) 做贡献的 \(j\) 要满足 \(r_j<l_i\),因此将所有区间按 \(r\) 排序后 \(j\) 就是一个前缀的形式，转移时二分出最大的 \(j\)，再维护一个前缀最大值即可完成转移。复杂度 \(n\log(n)\)。

trick：与排名有关，把不同分和同分分来考虑更清晰。

P2893 [USACO08FEB] Making the Grade G

题意：求把一个序列变成单调不降或单调不升的最小代价。

思路：有 \(O(n\log n)\) 的神仙做法。

考虑在维护序列的同时用优先队列维护当前修改过的序列的最大值，对于当前的数 \(x\)，那么先加入优先队列中，如果 \(x\) 比堆顶要小，我们就把 \(y\) 修改成 \(x\)，那么先加入优先队列中。

考虑为什么这样做是对的。如果有逆序对 \((i,j)\) ，那么 \(j\) 肯定不会减小，而我们也钦定了 \(j\) 不会减小，于是到达了下界。

现在有一个问题，如果修改后 \(y\) 前面的最大值大于 \(x\) 了，那么是否可以构造到达下界。我们可以把 \(x,y\) 都改成 \(y\) 前面的最大值，这样代价还是 \(y-x\)，于是可以到达下界。

trick：对于单调，可以考虑逆序对的影响。

P4409 [ZJOI2006] 皇帝的烦恼

题意：给定 \(n\) 个集合的大小，问在相邻集合没有交集的情况下，并集的最小大小。

思路：有很厉害的贪心做法。首先，答案肯定不小于相邻两项的和。其次，一个元素最多出现在 \(\left\lfloor\dfrac{n}{2}\right\rfloor\) 个集合里，于是答案有下界 \(\dfrac{\sum siz}{\left\lfloor\dfrac{n}{2}\right\rfloor}\)，这样就做完了。

trick：分析问题的上下界。

P8099 [USACO22JAN] Minimizing Haybales P

题意：给一个长度为 \(N\) 的数组 \(a\)，若相邻两数之差的绝对值不超过 \(K\) 则可以交换，问能得到的所有 \(a\) 中字典序最小的一个。

思路：考虑假设已经求出了 \(1\sim i-1\) 的答案，考虑新加进来的数，它能移动到的范围是最长的后缀满足所有数都在 \([h_i-k,h_i+k]\) 中，要最小化字典序，就要放在最左的满足 \(h_j>h_i\) 的数的左边。

以上操作都可以用平衡树维护，复杂度 \(O(n\log n)\)。

[AGC016D] XOR Replace

题意：给定序列 \(a\) 和 \(b\)，每次可以把 \(a\) 序列的一个数变成 \(a\) 序列的异或和，求把 \(a\) 变成 \(b\) 的最少的操作次数。

思路：发现第一次把一个数 \(a_i\) 变成异或和 \(S\) 后，此时的异或和是 \(a_i\)，因此每次操作相当于是把一个数变成上次被操作的数。简化一下，就相当于把异或和当做第 \(n+1\) 个数，每个操作可以把一个数和最后一个数交换。首先可以简单判断是否有解。接着考虑怎样让操作次数最小。发现这很类似排列的置换问题，于是考虑每对不同的 \(a_i,b_i\)，让 \(a_i\) 向 \(b_i\) 连边，最终答案即为边数 + 联通块数 -1。证明很简单，因为在同一连通块内可以用边数次完成，而从一个连通块到另一个连通块要花1的代价，一开始就在的连通块不用花这 1 的代价。复杂度 \(O(n\log n)\)。

trick：添加与全局相关的元素简化情况。

[AGC023F] 01 on Tree

题意：给出一棵 \(n\) 个节点的树，以及一个空序列。

• 每个节点上有一个取值在 \(\{0, 1\}\) 中的数。
• 每次你可以选择没有父亲节点的点删除，并且将这个节点上的数字放在当前数列末尾。
• 请你求出这个数列可能得到的最小逆序对数。

思路：对于两个点，假设管辖的 0,1 分别有 \(a_0,a_1,b_0,b_1\) 个，那么先选 \(a\) 的贡献就是 \(a1\times b_0\)，否则就是 \(a_0\times b_1\)，即当 \(\dfrac{a_1}{a_0}<\dfrac{b_1}{b_0}\) 时选择 \(a\) 在前。

于是用优先队列维护当前点的 \(\dfrac{a_1}{a_0}\) 的值，每次选择最小的和父节点合并即可。

trick：Exchange Argument

CF888G Xor-MST

题意：两点的边权是点权异或和，求 MST。

思路：可以贪心。如果建出 Trie 树，那么对于一个点的两个儿子，只需两边分别联通后，选一边的点，在另一边查异或最小值然后连起来就可以了。

P3457 [POI2007] POW-The Flood

题意：给定一张地势图，所有的点都被水淹没，现在有一些关键点，要求放最少的水泵使所有关键点的水都被抽干。

思路：首先，如果一个点周围比它低的点有抽水机，那么就不需要再放了。

于是可以把所有点按高度排序，如果从小到大依次判断四周连出去的点中是否有抽水机。这一步可以用并查集维护，把高的点放入四周低的点的并查集中，然后如果没有抽水机，就加一个抽水机。

trick：按照一定顺序对元素排序后再处理问题。

P9128 [USACO23FEB] Fertilizing Pastures G

题意：有 \(N\) 个顶点的树，经过节点之间的每一条边都需要 \(1s\)。每个顶点一开始的权值均为 \(0\)，第 \(i\) 个点的权值的增长速率为 \(a_i/s\)。FJ 从 \(1\) 号顶点出发遍历整棵树。当 FJ 走到某个节点时，若该节点的权值为 \(x\)，则需要支出大小为 \(x\) 的费用。（当然，只需在第一次经过该节点时需要支出。）

给出一个参数 \(T\):

• 若 \(T=0\)，FJ 必须回到 \(1\) 号节点。

• 若 \(T=1\)，FJ 可以在任意节点结束他的遍历。

求遍历所有节点的最小时间和此时需要付出的费用。

思路：假设我们当前已经求出了一个点的所有儿子的费用 \(f[i]\) 和增长速率和 \(s[i]\)，那么考虑相邻的两个 \(a,b\)，如果 \(a\) 在前，那么代价是 \(f[a]+f[b]+siz[a]s[b]\)，否则代价是 \(f[a]+f[b]+siz[b]s[a]\)，那么如果 \(siz[a]s[b]<siz[b]s[a]\)，即 \(\dfrac{siz[a]}{s[a]}<\dfrac{siz[b]}{s[b]}\) 时，\(a\) 在前更优。

于是就可以直接按照 \(\dfrac{siz[x]}{s[x]}\) 从小到大来取。

trick：exchange argument。

P8293 [省选联考 2022] 序列变换

题意：你手里有一个长度为 \(2 n\) 的合法括号序列 \(s\)。\(s\) 的每一个左括号有一个权值。形如 \(\texttt{(A()B)}\)（其中 \(\texttt{A}\)、\(\texttt{B}\) 均为合法括号序列，下同）的结构是你喜欢的，而形如 \(\texttt{(A)(B)}\) 的结构是你不喜欢的。你有两种操作来改变括号之间的位置。

这两种操作如下：

• 操作 1：交换形如 \(\texttt{p(A)(B)q}\) 的串中 \(\texttt{A}\) 和 \(\texttt{B}\) 之间的两个括号，变换为 \(\texttt{p(A()B)q}\)（其中 \(\texttt{p}\)、\(\texttt{q}\) 为任意串，可以为空，但不一定分别为合法括号序列，下同），它的代价为 \(x\) 乘 \(\texttt{(A)}\) 中第一个左括号的权值加上 \(y\) 乘 \(\texttt{(B)}\) 中第一个左括号的权值，其中 \(x, y \in \{0, 1\}\)；
• 操作 2：交换形如 \(\texttt{pABq}\) 的串中的 \(\texttt{A}\) 和 \(\texttt{B}\)，变换为 \(\texttt{pBAq}\)，这个操作不需要代价。

你现在想知道的是，将 \(s\) 变换为一个不包含你不喜欢的结构的括号序列至少需要多少代价？

思路：终于来写括号序列了。

首先是把括号序列转成括号树，那么操作 1 相当于是把拿出一个点的两个儿子 \(u,v\)，将 \(v\) 的儿子挂到 \(u\) 上，然后将 \(v\) 挂到 \(u\) 上，代价是 \(xa_u+ya_b\)，操作 2 就是可以任意交换儿子的权值。最终的状态就是整棵树是一条链。

其次，我们可以从上到下贪心，这样可以把尽量把贡献最小的节点向下传。

因为 \(x,y\) 的取值都只有 0/1，考虑分类讨论。

当 \(x=0,y=0\) 时，答案显然是 0。

当 \(x=0,y=1\) 时，考虑一个点的所有儿子，我们我们每次留下来的点不做贡献，那么每次留下来权值最大的即可，可以用 \(\text{multiset}\) 维护。

当 \(x=1,y=1\) 时，和上一种差不多，都是留下最大的点，不同之处在于先把其他点挂在最小的点上再挂到最大的点上，也可以用 \(\text{mulitset}\) 维护。

当 \(x=1,y=0\) 时，就不一定是留下来最大的点了，因为我们可以通过把最大的点不断下传来避免最大值做贡献。假设我们知道了留下来哪个点，那么剩下的步骤和上一种情况是一样的，代价是最小值乘上 \(siz-2\) 加上被留下来的值。那么除了被下传到最后一层的点，其他点都会做贡献，那么总贡献就是所有权值和减去下传到最后一层的点的权值加上每一层的最小值乘上 \(siz-2\)。于是我们在每一层要留下的点都不是最小值或者最大值。

当 \(siz=1\) 时，可以不用考虑。

当 \(siz>2\) 时，可以把最小值和最大值都下传。

当 \(siz=2\) 时，我们可以从全部的 \(siz\) 入手。全部的 \(siz\) 形如 \(2,2,2,>2,\cdots ,>2,\cdots,2,1\)，而且可以发现 \(siz=2\) 的层的代价就是留下来的点，那么代价就是所有点权值和减去下传的权值，从而有了枚举下传的权值的做法，复杂度是 \(O(n^2)\)。

考虑优化。我们可以从小到大枚举下传的点的权值，然后实时维护当前的权值下传后作为最小值的范围，可以做到 \(O(n\log n)\)。结合前面的下传最小值和最大值的结论，我们可以直接模拟下传最小值或者最大值的情况，就可以做到 \(O(n)\)。

trick：括号序列 \(\rightarrow\) 树。

P5290 [十二省联考 2019] 春节十二响

题意：给你一棵有 \(n\) 个节点的树，要求你将一个长度为 \(n\) 的序列划分成若干段，使得任意一段中没有两个数满足它们在树上是祖先——后代关系。请你求出每一段最大值之和的最小值。

思路：可以直接贪心，每个点维护一个堆表示选择的集合，每次合并用启发式合并即可。

「JOISC 2014 Day1」有趣的家庭菜园

题意：有一个序列 \(a\)，每次可以交换相邻两个数，求最小的交换次数使得序列是单峰的。

思路：从小到大考虑每个数，此时一个数左右两边比他大的数肯定是连续一段，那么直接将这个数移动到较短的那一段的端点即可，这样不仅单次是最优的，而且不会影响后面的数，所以是正确的。

复杂度 \(O(n\log n)\)。

trick：交换相邻项，可以按照冒泡的方法顺次考虑。

「JOISC 2014 Day4」挂饰

题意：JOI 君有 N 个装在手机上的挂饰，编号为 \(1\ldots N\)。 JOI 君可以将其中一些挂饰装在手机上。
JOI 君的挂饰有一些与众不同——其中的一些挂饰附有挂钩，你可以将其他挂饰挂在挂钩上。i 号挂饰有 \(A_i\) 个挂钩。每个挂件要么直接挂在手机上，要么挂在其他挂件的挂钩上。直接挂在手机上的挂件最多有 1 个。
此外，每个挂件有一个安装时会获得的喜悦值，用一个整数来表示。如果 JOI 君很讨厌某个挂饰，那么这个挂饰的喜悦值就是一个负数。
JOI 君想要最大化所有挂饰的喜悦值之和。

思路：根据 A,B 的正负性分类。

1. A>0,B>0，选择这些挂饰不仅会让答案变优，而且挂钩的数量也不会减少。
2. A=0,B>0，这些挂上后就不能再挂东西了，可以放在最后处理。
3. A>0,B<0，这些就是用来增加挂钩的数量的，那么对于每种挂钩的数量，我们只需知道挂饰最大的代价。

总结一下，就是先求出第一类贡献，然后用背包求出第三类挂饰的贡献，然后对于每种数量的挂钩，我们按贡献从大到小取第二类挂饰即可。复杂度 \(O(n^2)\)。

「JOISC 2015 Day 1」卡片占卜

题意：有 ABCDE 5 个数，表示有一个序列 \(a\)，顺次有 A 个 1，B 个 0，C 个 1，D 个 0，E 个 1，有 \(n\) 个区间，每次操作可以反转一个区间的 01，求最小的把序列变成全 1 的次数。

思路：做过类似的题目 Password，做法是大致相同的，就是用图论建模。

考虑对于一种操作 \([l,r]\)，连边 \(l\rightarrow r+1\)，这样我们可以用最短路求出反转任意区间的最小代价。

因为只用反转两个区间，反转的方式很少，可以简单判断。

trick：区间操作差分成单点操作。

「JOISC 2015 Day 4」防壁

题意：给定 \(n\) 个区间，有 \(m\) 次操作，每次要求所有区间在 \(p_i\) 处重合。对每个区间求出它的最小移动距离。

思路：神仙题。

首先，每个防壁的移动是独立的，每次移动是 \(O(1)\) 的，那我们就有了 \(O(nm)\) 的暴力做法。

接着我们先去掉一部分无用的激光。假设有连续 3 次激光的大小关系相同，如 \(p_i\le p_{i+1}\le p_{i+2}\)，那么我们在从覆盖 \(p_i\) 移动到覆盖 \(p_{i+2}\) 的过程中一定会经过 \(p_{i+1}\)，于是我们可以把 \(p_{i+1}\) 删掉。现在我们的 \(p\) 序列一定是波浪形的。

从上一步受到启发，如果防壁的长度极小，每一次都会移动 \(|p_{i+1}-p_i|\)，代价很好计算，进一步的，如果每一步都需要移动，我们是很容易求出总代价的，于是我们就要想办法变成每一步都要移动。

如果有 \(|p_{i+1}-p_i|\ge r-l\)，那么我们就一定要移动，否则我们尝试删掉一些点。我们考虑特殊的情况，\(|p_{i+1}-p_i|\) 是全局最小，不妨设 \(p_i\le p_{i+1}\)，那么我们从覆盖 \(p_{i-1}\) 到覆盖 \(p_{i+2}\) 的过程中，左端点一定会经过 \(p_i\)，那么此时就覆盖了 \(p_{i+1}\)，于是我们发现 \(p_i,p_{i+1}\) 没有贡献，可以删去。

注意边界情况。

1. 如果没有 \(p_{i-1}\) 和 \(p_{i+2}\) 那么不用删掉这两个点；
2. 如果没有 \(p_{i-1}\)，那么就不能删掉 \(p_{i+1}\)，因为左端点不一定在 \(p_i\)；
3. 如果没有 \(p_{i+2}\)，同上，不能删掉 \(p_i\)。

这个过程中我们要至少 3 个点，如果不到 3 个点可以暴力操作。

去掉了 \(|p_{i+1}-p_i|<r-l\) 的情况后，就可以简单的通过 \(\sum\limits_{i=2}^n(|p_{i+1}-p_i|-len)=\sum\limits_{i=2}^n|p_{i+1}-p_i|-(n-1)len\) 来求答案了。

上面的删除是按照 \(|p_{i+1}-p_i|\) 从小到大删除的，又因为防壁是独立的，我们可以按长度从小到大处理，这样我们需要删除的一定不会减少，每个 \(|p_{i+1}-p_i|\) 就只会被删掉一遍。

那么我们可以用可删除堆来取出最小的 \(|p_{i+1}-p_i|\)，用链表维护删除。复杂度 \(O(n\log n+m\log m)\)。

P3615 如厕计划

思路：首先找合法的充要条件。比如从后往前看，如果最后两个人都是男生，那么显然是不行的；我们一直推下去，就可以得出，如果把男生当做 1，女生当做 -1，那么条件就是后缀和不大于 1。

然后考虑我们怎么重排最优。我们的目的就是让男生尽量靠前，女生尽量靠后，那么可以每次把最后面的一个不合法的男生移动到开头，这样会让中间所有女生的代价加 1，会让后缀和加 1，那么我们需要 \(maxsuf-1\) 次，于是最终代价就是 \(maxsuf-1\)。

trick：找充要条件。

「JOISC 2016 Day 3」电报

题意：给出 N 个点，每个点的出度均为 1，给出这 N 个点初始指向的点 \(A_i\)，和改变这个点指向的目标所需要的价值 \(C_i\)。
求让所有点强连通的最小花费。

思路：发现考虑连边不好处理，但是考虑删边就更方便一些。如果一个点的入度大于 1，那么就需要删到只剩一条入边，我们肯定是贪心地保留最大的入边。

问题是可能会有环，那么我们就需要断掉一条环边，选择一条最大的非环边，那么就求出每个点最大的入边和不在环上的最大入边，取差最小的一个就行了。

复杂度 \(O(n)\)。

trick：添加不好处理，可以考虑变成删除。

「JOISC 2016 Day 4」最差记者 2

思路：到了贪心策略，而且是对的，只不过有线性做法，但是看不懂。

因为是要让改动尽量少，那么就是要让匹配的数量尽可能多，那么就直接找到能匹配的范围内有没有同国家的，有就直接匹配，否则就需要修改。复杂度 \(O(n\log n)\)。

「JOISC 2017 Day 1」烟花棒

题意：有 N 人站在一条数轴上。他们人手一个烟花，每人手中的烟花都恰好能燃烧 T 秒。每个烟花只能被点燃一次。
1 号站在原点，i 号 \((1\le i\le N)\) 到 1 号的距离为 \(X_i\)。保证 \(X_1=0，X_1, X_2, \dots, X_N\) 单调不降（可能有人位置重叠）。
开始时，K 号的烟花刚开始燃烧，其他人的烟花均未点燃。他们的点火工具坏了，只能用燃着的烟花将未点燃的烟花点燃。当两人位置重叠且其中一人手中的烟花燃着时，另一人手中的烟花就可以被点燃。忽略点火所需时间。
求至少需要以多快的速度跑，才能点燃所有人的烟花（此时可能有些人的烟花已经熄灭了）。

思路：显然可以先二分答案，关键是怎么判断是否合法。

有十分高妙的判定方法。首先，根据贪心，如果一个人会把另一个人点燃，那么这一个区间中的人都会被这个人点燃。因此，两个点 \((i,j)\) 可以在 T 秒内相遇当且仅当两点之间的距离大于 \(2tv(j-i)\)，那么我们可以先把 \(a_i\) 减去 \(2tvi\)，这样两点是否可达就可以直接判断。

判定分为两步。先从 \(k\) 开始往两边拓展，求出从 \(k\) 开始往左右各能拓展多远，然后从两端开始往中间拓展，最后如果一开始拓展的区间包含后面能拓展的区间就说明有解，否则就无解。本质就是从点燃区间 \([k,k]\) 开始拓展到其他区间，最后判断是否能够点燃区间 \([1,n]\)。

「JOISC 2019 Day1」馕

题意：给定长度为 M 的馕，和 N 个人，第 i 个人吃馕的第 j 米可以获得 \(V_i,j\) 的收益，现在需要将长为 M 的馕分成 N 段，每个人吃一段，使得每个人获得的收益至少为这个人吃掉整个馕的收益的 \(\frac{1}{N}\)，切的位置可以是分数。

思路：贪心好题。

考虑贪心。每次我们选择一个人肯定是要让它刚好取到 \(\dfrac{\sum v}{n}\) 最好，于是可以先求出每个人取 \(x\) 份最少需要多长，记为 \(p[i][x]\)，然后每次把当前段分给 \(p[i][x]\) 最小的人，这样前一段的结尾必然不超过 \(p[i][x-1]\)，这一段合法，而且也可以为后面留出更多的空间。容易看出，这样做必然是有解的。