构造题做题记录

1|0构造

感觉上很大一部分的构造题的构造过程可以画图，应该是一个不错的思考方向。

1|1P8098 [USACO22JAN] Tests for Haybales G

题意：有一个长为 $n$ 的不降的整数数组和一个整数 $k$,你不知道这个数组和这个整数，但你知道对于每个下标 $i$ 满足 $x_{j_i}\le x_i+k$ 的最大下标 $j_i$通过 $j$ 数组，构造一个任意数组 $x$ 和整数 $k$ 满足上述条件。

思路：考虑把这些关系放在树上，即$i\to j_i+1$，那么根一定是$n+1$，现在的限制是每个点比儿子的值大超过$k$，那么就想到每一层是$de{p}_i\ast k+r$，而$r$需要满足的是儿子的$r$比自己小，同层的$r$编号大的更大，那么就遍历儿子时先遍历大的，再令$r=K-dfn[i]$即可。

trick:遇到每个点有唯一前驱的条件，把树建出来问题可能会更好处理。

1|2[AGC018F] Two Trees

题意：给定两棵都是$N$个节点的有根树$A,B$，节点均从$1..N$标号。我们需要给每个标号定一个权值，使在两棵树上均满足任意节点子树权值和为$1$或$-1$输出任意一种解，需要判断无解。

思路：先声明取值只有 $-1,0,1$。

首先考虑每个最终权值的奇偶性，如果在两棵树上不同就无解。

接着考虑怎么构造。

我们把一对权值为$(1,-1)$的点当成一对匹配点，这样如果一个点有偶数个儿子，那么这些点可以一一匹配，否则就把当前点和未被匹配的一个儿子匹配。这样在两棵树上匹配的点对连边，容易发现是一个二分图，于是直接黑白染色就可以了。

trick：遇到确定权值的题，可以考虑通过缩小可选值域范围作为切入点。

1|3[AGC027F] Grafting

题意：给定两棵 $n$ 个节点的树 $A,B$，你需要对 $A$ 执行若干次操作，每次操作选择一个叶子节点，删除连接这个叶子的边，并将这个叶子节点连向任意一个另外的点，每个点只能被选择一次，求使得 $A,B$ 相同的最小的操作次数。

思路：首先，发现是无根树，于是考虑转成有根树。我们发现，如果进行完第一次操作，那么可以把第一次操作的点当成根，原因是这个点之后不会再做修改。

接着考虑构造。我们发现，根据只操作叶子的限制，在A树上，一个点必须比父节点先被操作，而在B树上必须后被操作，于是可以用拓扑排序求出一组合法解。

枚举第一次操作是$O(n^2)$的，于是总复杂度是$O(T{n}^3)$。

trick:从边界情况入手。

1|4[ARC095F] Permutation Tree

题意：给定一棵树 $\mathrm{T}$， 要求构造一个排列 $p$ 。对于每一个 $p_i$ ，找到最大的 $j$ 使得 $p_j<p_i$，然后在 $i,j$ 间连边。问是否可以构造出与 $\mathrm{T}$ 同构的树。如果可以，则给出字典序最小的排列。

思路：先考虑怎么生成排列。按权值从小到大枚举，把当前位置和最大值连边，并且更新最大值。

我们发现在连边过程中，会形成一阶毛毛虫，即一条链上挂一堆点，而且链上的点权值更大，下标更小。于是我们求出最长链及链上每个点的度数，假设当前已经有$S$个点已经排好，那么肯定是让$S+1$尽量靠前，于是就把当前链上的点放在$S+1+d_i$就行了。

1|5Largest Smallest Cyclic Shift

题意：定义 $f(S)$ 为：对于一个字符串 $S$，每次将它最左边的字符放置到字符串末尾生成的字符串集合中，字典序最小的字符串。例如：对于 $S$ 为 babca 的情况，$f(S)$ 即为 babca、abcab、bcaba、cabab、ababc 中最小的那个，即 ababc。

你需要构造一个字符串 $T$，共包含 $X$ 个字符 a、$Y$ 个字符 b 和 $Z$ 个字符 c，使得 $f(T)$ 尽可能大，输出这个 $f(T)$。

思路：设 $f(a,b,c,sa,sb,sc)$ 表示还剩 $a$ 个 $sa$，$b$ 个 $sb$，$c$ 个 $sc$ 时的答案，那么如果 $a,b,c$ 中只有两个有值，那么好处理；如果 $a>b+c$，那么在 $sb,sc$ 前面加上 $sa$ 再处理，如果 $a>c$ 那么这时 $sb$ 变成了 $sa+sc$，而 $sb$ 为 $sc$，其他情况可以类似处理。

1|6CF232C Doe Graphs

题意：$0$ 级 Doe 图是一个点，$1$ 级 Doe 图是两个点加一条边，$k$ 级 Doe 图是一个 $k-1$ 级 Doe 图加上一个编号全加了 $k-1$ 级 Doe 图大小的 $k-2$ 级 Doe 图再加上 $(1,|D_{i-1}|+1),(|D_{i-1}|,|D_{i-1}|+1)$ 两条边。给一个 $n$ 级 Doe 图，$m$ 次询问，每次查询 $a$ 和 $b$ 两点间的最短路。

思路：核心就是求出从某个点到1和$D_n$的最短路，然后递归求解$a,b$之间的距离$f(a,b,n,len)$。

如果$a,b⩽fib[n-1]$，那么就处理$f(a,b,n-1,2)$。

如果$a,b>fib[n-1]$，那么就处理$f(a-fi{b}_{n-1},b-fi{b}_{n-1},n-2,len-1)$

否则就有3种情况，$a\to 1\to |D_{n_1}|+1\to b$，$a\to |D_{n-1}|\to |D_{n-1}|+1\to b$，$a\to 1\to |D_{n-1}|\to b$。

1|7CF521E Cycling City

题意：给定无向图，问是否能找到两点满足这两点之间至少有 3 条完全不相交的简单路径。

思路：原条件等价与 dfs 树有一条边都被两条非树边。求出 dfs 树后，对于剩下的非树边，可以暴力覆盖，因为如果一条边被覆盖两次那么就找出了答案。细节略多。

trick:在无向图上的构造可以找出 dfs 树进行处理。

1|8CF566E Restoring Map

题意：给你一棵树每个点距离不超过 2 的点集，求出一颗满足条件的树。

思路：首先，如果两个点的邻居集合交集大小为2，那么交集中的点之间显然是有边的。这样所有非叶节点之间的连边都会被处理到，于是只用考虑每个非叶节点挂在哪里。

求出每个非叶节点的邻域，如果一个叶子节点的邻居集合和其相等，那么就挂在这个点上。

还有一个小点，就是对于每个叶子节点，包含了这个点的最小的集合就是这个点对应的集合。

1|9CF650E Clockwork Bomb

题意：给出两棵 $n$ 个节点的树，每次操作可以把第一棵树的一条边删掉然后连另外两个点，且必须满足每次操作完之后仍是一棵树。问最少需要多少步操作才能把第一棵树变成第二棵树（是完全相同，并不是同构），并输出方案。

思路：感觉这道题的思路比类似题更自然。

首先，如果一条边在两棵树上都出现过，那么显然这条边不会被处理，因此我们找到了操作次数的下界为 $n-1-c$，$c$ 为相同的边数。

将这些边连接的点合并后，就可以每次选在第一棵树里的叶子，然后连边，再不断递归下去。

实现方法很神仙，把第一棵树 dfs 一遍，对于一个节点 $x$，如果一个子节点 $y$ 和 $x$ 不在同一个连通块里，那么就找到 $y$ 和所在的连通块里深度最小的点 $d$，合并 $d$ 和 $d$ 的父节点。

trick：分析答案的上下界对解题方法有一定的启发。

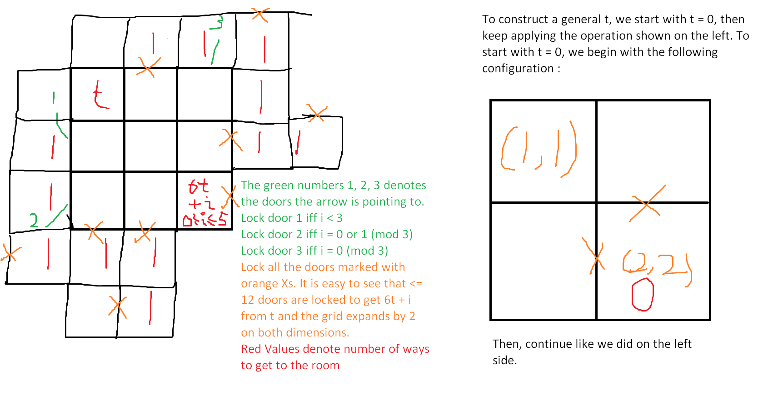
1|10CF715D Create a Maze

题意：有一个网格，你可以确定每条格线是否可以通信，要求最终从 $(1,1)$ 只向下向右走到 $(n,m)$ 的方案数为 k。

思路：和HBCPC的题几乎一样，做法有点小区别。

感觉说什么也不如这张图

构造题遇到大的数可以考虑按进制构造，而且不一定非要是二进制

1|11CF871E Restore the Tree

题意：有一棵树，你知道这棵树的 $k$ 个关键点与所有点的距离，要求还原出一棵满足条件的树。

思路：首先，显然是先求出所有关键点的虚树。可以任选一个点作为根，然后求出每个点的深度，这样就可以求出每个关键点及到根路径上的点的父节点。

再考虑不在虚树上的节点。我们找到离它距离最近的已经确定了的点，这样就可以再根据这个点的深度就可以知道树形态了。

1|12CF883B Berland Army

题意：$n$ 个点, $m$ 条有向边, 所有点的点权在 $1k$ 中且一部分点权已知, 希望确定一种方案满足:
1.对于所有由 $x$ 指向 $y$ 的边, $x$ 的点权大于$y$
2.对于 $i=1,2,...,k$ , 至少有一个点的点权为 $i$

思路：首先肯定是求出每个点可选权值范围 $[l_i,r_i]$，然后考虑填权值。我们从小到大枚举当前要填的权值 $x$，那么对于所有满足 $r_i=x$ 的 $i$，可以把权值填为 $x$，否则就找到最小的 $r_i$ 满足 $r_i>x$，把 $i$ 的权值填为$x$，这样就可以在满足权值大小关系的条件下尽量满足最后一个限制。

1|13CF1097E Egor and an RPG game

题意：设 $f(n)$ 表示满足所有长度为 $n$ 的排列都能被划分成 $k$ 个不相交的单调上升/单调下降子序列的 $k$ 的最小值，求出一种单调序列个数不超过 $f(n)$ 的划分方案。

思路：首先是结论：$f(n)$是满足$1+2+3\cdots x>f(n)$的最小的$x$。接下来考虑构造。

设当前LIS长度为 $l$，分两种情况。

一是 $l>f(n)$，那么 $f(n)$ 会减1，这样最多进行 $\sqrt{n}$ 次，这样复杂度是 $O(n\sqrt{n}\log n)$ 的

二是 $l⩽f(n)$，那么根据 $\text{Dilworth}$ 定理，最长反链等于最小链覆盖，于是直接找最小链覆盖即可。

对于找最小链覆盖的方法，可以发现在用二分求LIS的过程中就自然找出了LDS划分，这样就行了。

1|14CF1225F Tree Factory

题意：给出一棵树，每次操作可以将一个节点从它的父亲节点重新连到它的兄弟节点上，求将这棵树退化成链的最少步数，输出操作后遍历链的编号，最少操作次数，及每次操作的节点编号。

思路：因为感觉和深度相关，而且显然答案的下界是$n-maxdep$，因此考虑用长剖，这样操作时不需要操作最长链，就可以实现最小步数。

trick:同样是可以分析答案的上下界。

1|15CF1227G Not Same

题意：给定大小为 $n$ 的序列 $a$ ， 满足 $1⩽a_i⩽n$，你需要执行至多 $n+1$ 次操作使得所有数变为 $0$ ，每次操作你可以把一个子集的元素都 $-1$ ， 要求每次操作的子集互不相同。

思路：如果往矩阵方面想应该很容易想出来。（才看见输出的就是矩阵）

考虑把数列拆成 $(n+1)\times n$ 的01矩阵，那么每个数就代表着这一列的和是多少，而且要求每一行不相同。

我们把全 $n$ 数列的构造出来，那么矩阵大概是这个样子

$$\begin{array}{cccccccccc}& 0& 1& 1& 1& 1& 1& \cdots & 1& 1\\ & 1& 0& 1& 1& 1& 1& \cdots & 1& 1\\ & 1& 1& 0& 1& 1& 1& \cdots & 1& 1\\ & 1& 1& 1& 0& 1& 1& \cdots & 1& 1\\ & 1& 1& 1& 1& 0& 1& \cdots & 1& 1\\ & 1& 1& 1& 1& 1& 0& \cdots & 1& 1\\ & & & & & & & \cdots \\ & 1& 1& 1& 1& 1& 1& \cdots & 0& 1\\ & 1& 1& 1& 1& 1& 1& \cdots & 1& 0\\ & 1& 1& 1& 1& 1& 1& \cdots & 1& 1\end{array}$$

这启示我们可以第 $i$ 列从第 $i+1$ 个数开始填，但是还需先把所有数从大到小排序，因为排序后，对于任意两行 $i,j(i<j)$，如果要满足这两行相等，那么要求 $(j,i-1)=(i,i-1)=1$，而 $(i,i)=0$，$(j,i)$ 显然为 1，这样就不相等了。

1|16CF1375H Set Merging

题意：给定长度为 $n$ 的序列 $a$，最初有 $n$ 个集合 $\{a_1\},\{a_2\},\dots ,\{a_{n-1}\},\{a_n\}$。

• 接下来给定 $q$ 个询问，每次询问给出 $l,r$，你需要通过若干次操作制作出集合 $\{a_l,a_{l+1},\dots ,a_{r-1},a_r\}$。注意：操作过程中集合总数不能超过 $2.2\cdot {10}^6$。
• 操作是指：你可以合并两个集合 $A,B$，但要满足 $\underset{u\in A}{max}u<\underset{u\in B}{min}u$。注意：合并后集合 $A,B$ 依然存在。

思路：有两种主流做法，一种是值域分块，一种是线段树。没有看懂值域分块的做法，只会线段树的做法。

首先考虑最朴素的暴力，就是把所有的数排序后依次合并，接着可以考虑把这一步放在值域线段树上维护，每次往底层分治下去再合并。

然后考虑优化，即如果一个区间之前已经被合并出来过那么就可以不用额外处理，这样可以证明复杂度是对的，因为层数大于 $\frac{Q}{2}$ 的即使跑满也不到 $2^{n+\frac{Q}{2}}$，剩下的最多是 $q{2}^{n-\frac{Q}{2}}=2^{n+\frac{Q}{2}}$。

trick:遇到合并可以往分治方面去想。

1|17CF1474E What Is It?

题意：给定一个 $n$，你需要构造一个排列 $\{p_i\}$ 和一个操作序列。每次操作你可以交换 $i$ 和 $p_i$，并获得 $(p_i-i{)}^2$ 的贡献。你需要最大化总贡献。

思路：想到了大概，就是拆成构造一个长为 $n$ 的置换环，然后就不太好构造了。

接下来的构造就是 $1\to n\to n-1\cdots \lfloor \frac{n}{2}\rfloor +1\to n\to 2\cdots \lfloor \frac{n}{2}\rfloor$，可以达到 $(n-1{)}^2+2((n-2{)}^2+(n-3{)}^2\cdots )$ 的上界。

证明可以考虑，$(n-1{)}^2$ 最多被贡献一次，而且 $(n-2{)}^2$ 最多被贡献两次，接着的数因为前面的已经到了上界因此最多贡献两次。

trick:同样是可以分析答案的上下界。

1|18CF1500C Matrix Sorting

题意：给你两个 $n\times m$ 的矩阵 $A,B$（$1\le n,m\le 1500$），矩阵的元素均为 $[1,n]$ 内的整数。每一次操作你可以选定一列作为每一行的关键字，按照关键字从小到大的顺序把所有行排序得到一个新矩阵。这里使用的排序是稳定的，即如果有两行的关键字相同，则按照在原矩阵的先后顺序排序。要求构造一组方案。

思路：离谱题。没人知道这个做法为什么是对的，但是它就是对的。

首先每一列至多被操作一次。先在B中随机找一个不降的序列作为最终序列，然后再找满足对于每个相同数的连续段的相对次序都合法的列进行操作，用bitset优化即可。

1|19CF1592F1/2 Alice and Recoloring

思路：自己和同学推出来了只用1、4操作，然后发现两次4操作不如6次1操作，于是以为只需要用1操作。

实际上可能会用一次。

有一个没想到的简单trick：令 $b[x][y]=a[x-1][y-1]\oplus a[x-1][y]\oplus a[x][y-1]\oplus a[x][y]$，这样1操作相当于单点翻转，4操作相当于翻转4个点，于是直接判有没有满足条件的4操作然后把答案减1就行了。

对于F2，每一行、列只会用一次，这样直接求一个匹配就可以了。

trick：遇到对整体的操作，要想办法变成对单点的操作，通常可以用差分来转化。

1|20CF1599A Weights

题意：给你一个长度为 $N$ 的质量为 $A_1$, $A_2$ ... $A_N$ 的数组 $A$。每个数组中的值表示各个砝码的重量。 所有砝码的质量均不相同。你可以把每个砝码放在天平的一边（左边或右边）。还有一个由字符 "$L$"和 "$R$"组成的字符串 $S$ ，意思是在放完第 $i$ 个砝码（不是 $A_i$ ，而是选择第 $i$ 个砝码）后，天平的左边或右边应该更重。 找出在天平上放置砝码的顺序，以便满足字符串 $S$ 的规则。

思路：想到了可以从小到大排序后LRLR放，不过对于更一般的情况没有太好的想法。

有一个结论，如果最后是R，那么第1,3,5,7...大的肯定放在右边。于是只需考虑顺序。

可以从后往前倒推，如果连续的两个相等就填最小的否则就填最大的，用双端队列即可。

trick：从边界情况入手。

1|21CF1599J Bob's Beautiful Array

题意：你有一个长度为 $n$ 的数组 $B$，你需要构造一个长度为 $n$ 的数组 $A$，使得 $B$ 中每一个元素都能由 $A$ 中两个位置不同的元素相加得到。

思路：神仙题。

我们倒着考虑。如果我们构造出了答案序列 $x$，那么我们把所有 $x_i+x_j\in A$ 的 $i,j$ 之间连边，就是一个基环树，这样只要构造出环问题就迎刃而解。

首先，如果有偶数，那么如果有至少两个奇数或者没有奇数，那么可以直接构造一个大小为3的奇环。

否则就需要构造一个偶环。考虑把这个偶环上的边黑白染色，那么就要求黑边的权值和等于白边的权值和，即 $A$ 中存在两个大小相等的不交集合的大小相等。可是直接背包显然是不现实的。我们发现，$(\genfrac{}{}{0ex}{}{13}{27})>13\times {10}^6$，这就意味着任意长度不小于27的序列都存在合法解，于是我们取前 $min(n,27)$ 个，再折半搜索就可以了。

trick：一个元素与若干其他元素相关可以考虑建图处理。

1|22P7115 [NOIP2020] 移球游戏

题意：给定 $n+1$ 个栈，栈的高度限制为 $m$。初始时前 $n$ 个上每个有 $m$ 个球，最后一个为空。球分为 $n$ 种颜色，每种恰好 $m$ 个。一次操作可以把一个栈顶的元素弹出放到一个另一个栈顶，但是不可以使栈溢出或下溢。现要把同种颜色的球移动到同一个栈上，你需要构造一个在 820000 次操作内的方案。

思路：终于来写移球游戏了。

自己想到了一个神秘方法，每次选择一个代价最小的颜色归位，不知道能不能过。

有一个分治的做法。首先，假设当前只有两列，设第一根柱子上颜色为 1 的有 $a$ 个，那么可以进行4不操作：

1. 把第二根柱子的前 $a$ 个放到第三根上。

2. 把第一根的所有 1 放到第二根上，颜色为 0 的放到第三根上。

3. 把第二根上的 1 放到第一根上，再把第三根的 0 放到第一根上，把第二根剩余的放到第三根上，再把第一根的 0 放到第二根上。

4. 最后把第三根上的 01 放到第一、二根上就行了。

trick：对于类似排序的问题，可以考虑转成 01，也不能忘了归并排序。

1|23[AGC030C] Coloring Torus

题意：给定一个数字 $K$，你需要构造一个 $n\times n$ 的矩阵 $A$，需要满足以下条件：

• $n\in [1,500]$。
• $\mathrm{\forall }i,j\in [1,n],A_{i,j}\in [1,K]$ 且为整数。
• $\mathrm{\forall }v\in [1,K],\text{exist}i,j\in [1,n],A_{i,j}=v$。
• 设 $cn{t}_{i,j,v}$ 表示 $A_{imodn+1,j},A_{i,jmodn+1},A_{(i-2)modn+1,j},A_{i,(j-2)modn+1}$ 四个数中等于 $v$ 的数的个数。那么对于矩阵中任意两个数 $A_{i,j}$ 和 $A_{x,y}$，若 $A_{i,j}=A_{x,y}$，则需要满足 $\mathrm{\forall }v\in [1,K],cn{t}_{i,j,v}=cn{t}_{x,y,v}$。
  求出任意一个合法的方案即可。

思路：巧妙的构造题。

想到了沿对角线放。

正解就是沿着对角线放，大概长这样：

$$\begin{array}{cccccc}1& 2& 3& 4& \dots & n\\ 2& 3& 4& \dots & n& 1\\ 3& 4& \dots & n& 1& 2\\ 4& \dots & n& 1& 2& 3\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ n& 1& 2& 3& \dots & n-1\end{array}$$

这样还是需要$K\times K$的矩阵，不过我们发现可以每一个对角线可以间隔放两种数，就像这样：

$$\begin{array}{cccccc}1& 2& 3& 4& \dots & n\\ 2& 3& 4& \dots & n+1& 1\\ 3& 4& \dots & n& 1& 2\\ 4& \dots & n+1& 1& 2& 3\\ ⋮& ⋮& ⋮& ⋮& ⋮& ⋮\\ n& 1& 2& 3& \dots & n-1\end{array}$$

1|24[ARC089E] GraphXY

题意：给出一个$A\times B$的矩阵，其中第$i$行第$j$列元素为$d_{i,j}$。试构造一个有向图，满足：

1、有向图点数$\le 300$；

2、图中没有自环和重边；

3、图中边有边权，边权为 $[0,100]$ 中的整数，或者是未知数X或Y；

4、对于所有$x\in [1,A],y\in [1,B]$，满足当未知数$X=x$，$Y=y$时，图中$S$到$T$的最短路为$d_{x,y}$。

思路：小清新构造题。

设 $f[i][j]$ 表示 $S$ ~ $T$ 的路径上有 $i$ 个 $x$ 和 $j$ 个 $y$ 时其余边的最小可能长度，那么有 $f[i][j]$ 可以推出 $d[x][y]=min(f[i][j]+ix+jy)$，从这个可以推出 $f[i][j]=max(d[x][y]-ix-jy)$，如果求出 $f[i][j]$ 但是不满足条件，那么就无解，否则就一定有解。

考虑怎么构造。其实比较自然，因为钦定了经过多少条 $x,y$ 的边，所以可以构造两条长为 100 的链，对于一对 $(i,j)$，从 $x$ 链的 $i$ 号节点连一条 $f[i][j]$ 的边连向 $y$ 链上的倒数第 $j$ 号节点即可。

trick：如果构造遇到未知数，可以通过 DP 等方式求出未知数的线性组合的贡献。

1|25CF1329D Dreamoon Likes Strings

题意：我们称一个字符串 $s_1,s_2,\dots ,s_n$ 是美丽的，当且仅当对于任意 $1\le i<n$，$s_i\ne s_{i+1}$。初始时，Dreamoon 有一个字符串 $a$。在每一步内，Dreamoon 可以选择 $a$ 的一个美丽的子串，然后移除它，再将剩余的字符按照原来的顺序连接起来。要求用尽可能少的步数使得 $a$ 变成空串。

思路：神仙转化题。

一开始想到了一堆复杂度很高的DP，都过不去。

正解先是一步转化。把所有相邻且相等的位置拿出来组成一个新串，相当于是把可以随意被消掉的部分去掉了。此时对于原串的操作相当于是把新串的一个字符去掉或者消掉相邻的两个不相同字符，这样剩下只需对原串再进行一次操作即可。

转化完后就比较容易了。可以理解成一个类似匹配的问题。设所有字符中出现次数最大的为$x$，如果$2cn{t}_x⩾sum$，那么就让所有其他字符消去$x$，再直接消$x$，否则就每次找两个相邻且不同的字符消掉直到变成第一种情况。

具体实现可以用栈。有点小细节。

trick：简化无用的状态。

1|26CF1481F AB Tree

题意：给定一棵 $n$ 个节点的树，根为 $1$ ，每个节点会分配到一个字符 a 或 b。

要求整棵树中字符 a 的数量为 $x$ ，字符 b 的数量为 $n-x$ 。

定义节点 $v$ 上的字符串：

• 若 $v$ 是根节点，则 $v$ 的上的字符串为根节点分配到的字符。

• 否则，$v$ 上的字符串为父节点上的字符串的末尾加上 $v$ 分配到的字符。

请为每个节点分配字符，在满足字符 a ，b 数量要求的前提下，使得所有节点上的字符串的种类最少。

思路：又是背包题。

自己想的是尽量让靠近根的颜色一样，结果是尽量让每一层的颜色一样，确实是更优。

首先，假设有一种选取方法使得一些层数对应节点数之和为 $x$ ，那么就可以直接处理，答案为 $maxdep$，否则会有一层节点既有 A 又有 B，你我们的任务就是让每一层的非叶节点尽量为一种颜色。我们发现存在构造使得可以达到 $maxdep+1$ 的上界。

具体地，对于每一层，我们先考虑非叶节点，设节点数为 $l$，剩下可以用的字符有 $res$ 个，那么首先有 $l⩽\frac{res}{2}$，因此一定能找到一种颜色使得可以填完这些非叶节点。接着考虑叶子节点，如果可以用和刚刚一样的颜色就用，否则就和剩下的节点都用同种颜色。这样只会有一层的叶子节点会不一样，因此答案就是 $maxdep+1$。

trick：分析答案的上下界。

1|27CF1667C Half Queen Cover

题意：给定一个 $n\times n$（$1\le n\le {10}^5$）的棋盘，将第 $i$ 行第 $j$ 列的坐标记作 $(i,j)$。至少需要多少个半皇后，才能使棋盘上每个格子都被攻击到？输出它们的坐标。

注：一个点$(c,d)$ 能够被处于 $(a,b)$ 的半皇后攻击到，当且仅当 $a=c$ 或 $b=d$ 或 $a-b=c-d$。

思路：一开始把题目看错了，推了半天推不出来。

其实思路比较简单，就设答案为 $k$，那么把前 $k$ 行 $k$ 列用皇后填满，考虑同时把剩下的 $2(n-k)-1$ 个对角线填满，如果达到上界的话就是 $k\ge 2(n-k)-1$，即 $k\ge \lfloor {\displaystyle \frac{2n+1}{3}}\rfloor$。

然后考虑像马走日字一样放 $(1,1),(3,2),(5,3)\cdots$，这样可以覆盖非负的对角线，然后再在偶数行也用类似的方法就行了。

trick：分析答案的上下界，考虑用一些实际方法（经验）来构造。

1|28P6726 [COCI2015-2016#5] POPLAVA

题意：使得柱状图的容量为 $X$ 。如果不存在，则输出 $-1$。否则输出任意一种方案

思路：考虑最大容量，那么就是把 $n-1,n$ 放在两边，这样容量就是 ${\displaystyle \frac{(n-1)(n-2)}{2}}$。

接下来考虑怎么构造。在 $n,n-1$ 之间的柱子，每个的贡献是 $n-1-i$，于是我们就是要用 $\{1,2,\cdots ,n-2\}$ 构造出 $X$，令剩下的不做贡献即可。这一步可以每次选择最大的可以放进来的柱子，可以证明是对的。

trick：不妨先假设一定可以构造出来，再证明。

1|29P7007 [CERC2013] Rubik's Rectangle

题意：有一个 $h\times w$ 的棋盘，每个位置上有一个在 $[1,h\times w]$ 的整数，且没有重复。每次操作可以翻转一行或一列（顺序上翻转）。输出一行一个操作序列，使得操作后矩阵满足从上到下，从左到右递增。

思路：套路和魔方很像的构造题。

首先，可以发现 $(x,y),(n-x,y),(x,n-y),(n-x,n-y)$ 这 4 个格子无论怎么操作都还是在这 4 个位置上，于是我们就只用可以每一组怎么操作。

对于 $\left[\begin{array}{cc}a& b\\ c& d\end{array}\right]$，如果操作 $a$ 所在的点，就是 RCRC 或者 CRCR，会让 $b,c,d$ 顺时针或逆时针旋转，于是每次先把 $a$ 归位，然后把 $b$ 归位，最后判 $c,d$ 是否合法即可。

trick：找出等价类。

1|30CF1559D2 Mocha and Diana (Hard Version)

题意：给定图 $A$，$B$，每次操作可在两图内加边 $(u,v)$，要求两图仍为森林。求最大操作次数和一种方案。

思路：首先可以证明，最终一定有一个图只有一个连通块。

如果 A 中连通块数大于 1，那么对于任意两个连通块，在 B 中一定都联通，于是 B 中一定只有一个连通块，否则 A 就是一个连通块。

因此可以随意加所有可行边。

这样做是 $O(n^2\alpha (n))$ 的。考虑怎么优化。

我们把所有点都与一个点连边，然后把剩下的不与这个连通块连通的随意匹配即可。

1|31code_festival_2017_quala_d Four Coloring

题意：给一个 $n\times m$ 的网格，要求 4 染色，使得任意一对曼哈顿距离为 $d$ 的格子颜色不同。

思路：考虑转成切比雪夫距离，那么相当于是一个点和一个正方形边框中的点颜色不同，于是可以分成 $d\text{time}d$ 的网格，每个大网格中的点的颜色一样，这样只要相邻两个大网格颜色不同即可。

trick：曼哈顿距离和切比雪夫距离的相互转化。

1|32[AGC027D] Modulo Matrix

题意：构造一个 $n\times n$ 的矩阵，要求满足：每个元素不超过 ${10}^{1}5$ 且互不相同，对于任意两个相邻的数 $(x,y)$，$max(x,y)\mathrm{mod}min(x,y)$ 必须相等。

思路：我也不知道这么人类智慧的做法是怎么想出来的。首先，把这个矩阵黑白染色，钦定白格子的数是所有相邻的数的 $\text{lcm}+1$，那么可以很好的满足后两个条件。接着考虑用质数来填上面的数，不过这样做要用 $O(n^2)$个 质数，白格子的数可能超出范围，于是就要想办法用尽量少的质数来完成这件事。考虑这样一种构造，给每条黑格子所在的对角线分配一个质数，这个黑格子的数就是这两个质数的乘积，再简单调整一下顺序，这样就可以保证数字大小不超过 ${10}^{1}5$。

1|33CF612E Square Root of Permutation

题意：给定一个 $n$ 的排列 $p_i$，构造一个排列 $q$，使得对于任意 $1\le i\le n$，$q_{q_i}=p_i$。无解输出 $-1$。

思路：考虑有一个环 $p_1\to p_2\to p_3\to \cdots p_k\to p_1$，

如果 $k$ 是奇数，那么平方就是 $p_1\to p_3\to p_5\cdots p_k\to p_2\to p_4\cdots \to p_k-1$

如果 $k$ 是偶数，那么平方就是 $p_1\to p_3\to p_5\cdots p_k-1$ 和 $p_2\to p_4\to \cdots p_k$。

因此如果环长是奇数，可以直接还原出来，否则就需要两个大小相同的环拼起来。

trick：把构造的过程反过来考虑。

1|34CF512E Fox And Polygon

题意：n边形的一种“分法”是n - 3条不相交的对角线构成的集合。

每一步可以选择一条对角线（但不能是n边形的边）然后翻转这条对角线。

对于一条对角线AB，假设它的两边分别是三角形ABC和三角形ABD。“翻转”对角线AB，就是删除对角线AB，并添加对角线CD。

给定初始状态和终止状态，操作次数限制 20n 次。

思路：这种题有很经典的套路：找到一个中间状态，让初始状态和终止状态都变成中间状态。

在这一题中，中间状态可以就是所有对角线都与 1 相连。

考虑怎么构造。

如果 1 连了 $i$ 但没有连 $i+1$，下一个连的是 $j$，那么 $i,j$ 之间肯定有边，于是直接操作 $(i,j)$ 即可。次数为 $2(n-2)$。

trick：给定初始态和终止态，可以找到一个容易到达的中间态，让两个状态都变成中间态。

1|35CF468C Hack it!

题意：找到一对 $l,r$，满足 $[l,r]$ 中的数的数码和是 $a$ 的倍数。

思路：很巧妙的思维题。

我们发现，$f(x)+1=f({10}^{18}+x)$。记 $g_{l,r}=\sum _{i=l}^{r}f(i)$，那么可以发现$g_{1,{10}^{18}}\equiv g_{0,{10}^{18}-1}+1(\mathrm{mod}a)$，于是有 $g_{l,{10}^{18}-1+l}\equiv g_{0,{10}^{18}-1}+l(\mathrm{mod}a)$，于是记 $g_{0,{10}^{18}-1}\equiv p(\mathrm{mod}a)$，我们只需取 $l=a-p,r={10}^{18}+a-p-1$ 即可。

现在的问题是计算 $p$，可以发现就等于 $81\times {10}^{18}$，于是就做完了。

trick：考虑边界情况。

1|36P3599 Koishi Loves Construction

题意：构造 $1\sim n$ 的排列，① 求出能否满足 $n$ 个前缀和在模 $n$ 的意义下互不相同；② $n$ 个前缀积在模 $n$ 的意义下互不相同。

思路：对于第一问，如果 $n$ 是奇数，那么 $1\sim n$ 即可。否则可以发现奇数时是 $n-i+1$，否则是 $i-1$。

对于第二问，首先可以发现 1 一定在第一个，$n$ 一定在最后，而且 $\prod _{i=1}^{n-1}i$ 不是 $n$ 的倍数。

打表可以发现只有 1,4 和质数是有解的，而且可以构造出前缀积是 $1\sim n-1$，于是反过来用根据逆元来推是哪个数即可。

1|37P6831 [IOI2020]嘉年华奖券

题意：有 $n$ 种颜色的奖券，每种 $m$ 张，每张有价值 $a[i][j]$，有 $k$ 轮，每轮第要从每种剩下的里面挑各挑一张，设这 $n$ 张的中位数为 $x$，那么可以获得 $\sum _{i=1}^n|a_i-x|$ 的价值，求 $k$ 轮总价值的最大值和方案。

思路：首先考虑，假如我们知道了我们总共用了哪些奖券，那么其中有 $\frac{nk}{2}$ 个取正贡献，$\frac{nk}{2}$ 个取负贡献，并且每一轮中取负贡献的比取正贡献的值小。这样就可以推出，一定存在一组最优解满足可以把这 $nk$ 个数分成 $k$ 组，使得每组中的 $n$ 张奖券的颜色互不相同。

于是先要确定选哪些奖券。这一步可以直接贪心，先默认取负贡献，然后再贪心地把 $\frac{nk}{2}$ 个变成正贡献即可。

接着就是如何构造方案。设一种颜色取正贡献的有 $cn{t}_i$ 张，那么每一轮取 $cn{t}_i$ 前 $\frac{n}{2}$ 大的取正贡献，否则取负贡献，一直递归下去就可以了。

__EOF__

本文作者：Xttttr
本文链接：https://www.cnblogs.com/Xttttr/p/18015993.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！