网络流做题记录

1|0网络流做题记录

主要用来记录除了网络流24题之外的网络流题目。

1|1P4126 [AHOI2009]最小割

题意：对于每条边，求①这条边有没有可能在一种最小割中②这条边是不是一定在所有最小割中。

思路：首先看第一问。首先可以想到，如果一条边没有满流，那显然不能在最小割里。那如果满流的边一定在最小割里吗？其实不是。如果这两个点在同一个强连通分量里，那么可以让流沿着环流一遍，这样这条边就不满流了，不满足条件。于是，有可能在最小割里的充要条件是满流且两端不在同一个强连通分量里。

再看第二问，首先肯定也得满足满流的条件。其次，要满足源点可以到入点，出点可以到汇点，因为如果有一边到不了那说明在这条路径上存在一条同样可以被断掉的边，且也满足是最小割。因此可以推出，只有源点和入点在同一个强连通分量里，出点和汇点在同一个强连通分量里才能满足条件。这就是充要条件。

在实现上，先dinic再跑一编tarjan即可。

1|2P3731 [HAOI2017]新型城市化

题意： $n$ 个点 $m$ 条边的完全图的补图，对于每条边询问删掉这条边后原图最大团大小会不会增加。

思路：首先，因为题面中的限制，这个图可以被看成二分图，因此补图的最大团等于二分图最大独立集，证明可以考虑独立集里的点在原图中两两都有边，与一个团对应。又根据经典的结论，二分图最大独立集=点数-最小覆盖集=最大匹配，因此原题意就变成了求每条边删去后最大流是否改变。直接用上一题的做法即可。

1|3P5331 [SNOI2019]通信

题意：有 $n$ 个基站要通信，每个基站可以直接用 $w$ 的代价与控制中心相连，也可以选择前面一个没有没连过给基站，代价是 $| a_{i} - a_{j} |$ ，求最小总代价。

思路：首先有一个很明显的拆点后 $O (n^{2})$ 建边后跑费用流的做法，但 $n^{2}$ 条边肯定会T，于是考虑优化建边。例如，可以考虑把 $a_{i}$ 排序后依次相连，用累加差来表示代价，但这样不好确定每个点拆出来的点中哪个与这些点相连，于是考虑分治。对于区间 $(l, r)$ ， $(l, m i d)$ 的点拆除来的出点与表示代价的点相连， $(m i d + 1, r)$ 的点拆出来的入点与表示代价的点相连，然后跑费用流就可以了。

1|4P5192 Zoj3229 Shoot the Bullet|东方文花帖|【模板】有源汇上下界最大流

题意：~~（这题目怎么这么长）~~ 有 $n$ 天，每天最多拍 $D_{i}$ 张照片，有 $C_{i}$ 个取材对象，每个取材对象 $T_{i, j}$ 需要拍 $[L_{i, j}, R_{i, j}]$ 的照片，同时 $m$ 个少女中每个少女的照片数量不得少于 $G_{i}$ 。

思路：既然是模板那就按模板来写。

1|0无源汇上下界可行流

这是上下界网络流中最简单的一种，给定一个没有源点和汇点、每条边的流量有上下界的流量网络，问是否存在一种可行流使得流量平衡，即每个点的流入量等于流出量。我们的做法是，把它拆成两个网络，一个每条边的容量是下界（下界网络），另一个每条边的容量是上下界之差（差网络），这时条件就是两个网络的流量之和是一种可行流。首先，下界网络肯定得满流，但是这样不一定是可行流，于是可以通过差网络把这些不平衡的地方补上。具体地，我们在差网络中新设一个源点和汇点，如果一个点在下界网络里流入量比流出量多 $Δ$ ，那么就从在差网络中由源点向这个点连一条容量为 $Δ$ 的附加边，如果流出量比流入量多 $Δ$ ，就由这个点向汇点连容量为 $Δ$ 的附加边。这时再跑差网络的最大流，如果满足每条附加边都满流，那么这就是一个可行流；反之，就不存在可行流。

在代码实现的时候，不用把下界网络建出来，直接在差网络上跑就行。

1|0有源汇上下界可行流

虽然是有源汇，但其实很简单。我们考虑，如果汇点向源点连容量为 $i n f$ 的边，再跑无源汇上下界可行流，就等价与求了一个有源汇上下界可行流。

1|0有源汇上下界最大流

这才是一般在实际应用中使用的。要求最大流，我们可以在差网络中把附加边删掉，求残量网络的最大流，再加上之前的可行流就是答案。证明可以考虑我们新找的最大流一定是平衡的，再加上原来的可行流也是可行流。

在实现上，其实不需要真的把附加边删掉，因为除了汇点连向源点的边其他的都已经满流了，对答案没有影响，因此只需删汇点连向源点的边即可。

现在再来看这道题，其实建模很朴素，源点向每一天连 $[0, D_{i}]$ 的边，
每一天向每个少女连 $[L_{i, j}, R_{i, j}]$ 的边，每个少女向汇点连 $[G_{i}, i n f]$ 的边，然后跑有源汇上下界最大流即可。

1|5P4843 清理雪道

题意：求有向图最小链覆盖，每条链可以相交。

思路：一开始以为就是最小链覆盖，结果样例一直过不去，手推出来发现确实有问题，然后才发现问题。考虑建模，每条边最少被覆盖一次，于是可以源点向每个点连容量为 $i n f$ 的边。每个点向汇点连容量为 $i n f$ 的边，对于原图上的边 $(x, y)$ ，从 $x$ 向 $y$ 连 $[1, i n f]$ 的边，然后跑有源汇上下界最小流即可。等等，这里是最小流，不是最大流，那怎么求呢？

1|0有源汇上下界最小流

可以类比有源汇上下界最大流的做法，只是要从汇点到源点跑一遍最大流，再用可行流减去最大流就是答案。

1|6P4043 [AHOI2014/JSOI2014]支线剧情

题意：DAG最小链覆盖，要求每条链的开头是1号点，有边权。

思路：一开始以为就是上一题然后改流量，结果发现有边权不好处理。于是考虑用费用流。这时就需要用上有源汇上下界费用流

1|0有源汇上下界费用流

其实理论上是有源汇上下界最小可行费用流，也就是不一定是最大流。

具体做法其实和前面的很像。对于一条边 $(u, v, [l, r], c o s t)$ ，建边 $(u, v, r - l, c o s t)$ ，并且把答案加上 $l \times c o s t$ ，同样，如果 $i n [i] > o u t [i]$ ,建边 $(S, i, i n [i] - o u t [i], 0)$ ，反之则 $(i, T, o u t [i] - i n [i], 0)$ ，最后建边 $(T, S, i n f, 0)$ ，再跑 $(S, T)$ 的最小费用流，加上之前累计的答案即可。~~（确实是很像）~~

1|7P4553 80人环游世界

题意： $n$ 个城市，最多 $m$ 个人，每个人可以按 $1$ ~ $n$ 顺序选择若干个城市依次游历，每个城市恰好被 $v_{i}$ 个人经过，从 $i$ 到 $j$ 代价为 $w_{i, j}$ ，求最小代价。

思路：一开始想的时候在最小费用最大流和有源汇上下界最小费用可行流之间纠结，然后写了后者，发现过不了样例，于是就去写前者，发现建模其实很简单，只是要额外建一个点表示哪些人从哪个城市开始就可以了。

1|8CF277E Binary Tree on Plane

题意：平面上有 $n$ 个点，要求用这些点组成一个二叉树，且每条边都是从 $y$ 坐标大的点向 $y$ 坐标的点，权值是两个点的欧几里得距离，求最小总权值。

思路：比较简单的费用流建模。拆点，源点向1连容量为 $n - 1$ ，费用为0的边，除1以外的所有点向汇点连容量为2，费用为0的边，其他每个点向可以到的点连容量为 $1$ ，费用为 $d i s$ 的边，跑最小费用最大流，如果最大流 $\neq n - 1$ ，就无解，否则费用为答案。~~（有人写zkw一直寄但是一改成EK就过了，比较离谱）。~~

1|9P5030 长脖子鹿放置

题意：给一个 $N \times M$ 的棋盘，有一些格子是障碍，长脖子鹿按照“目”字攻击，求最多可以放多少个互不攻击的长脖子鹿。

思路：类似骑士共存问题，只是这次二分图判定标准是行（或列）的奇偶性。

1|10P4412 [SHOI2004] 最小生成树

题意：一张无向图，给定一棵生成树，求最小的修改边权的代价使得这棵生成树是最小生成树，代价定义为修改前后一条边的边权变化量的绝对值。

思路：首先，发现让这棵树成为最小生成树不好直接处理，但是判定是否为最小生成树却相对更容易。判定的思路也很简单，对于每一条非树边 $(x, y)$ ，树上 $x$ 到 $y$ 的路径上的任意一条边边权都不能超过这条非树边的边权。

显然，树上的边边权一定不会减小，非树边边权一定不会变大。于是对于一条非树边 $y$ 和在树上的一条边 $x$ ，有 $w_{x} + | Δ x | ⩾ w_{y} - | Δ y |$ ，即 $| Δ x | + | Δ y | ⩾ w_{y} - w_{x}$ 。那我们把每一条边当做一个点，点权就是原来的边权，发现原问题就是最小顶标号问题，直接求二分图最大权完美匹配可以了。

由于不会写KM算法，就写了费用流。

1|11CF884F Anti-Palindromize

题意：对于一个字串 $a$ ，若其长度 $m$ 为偶数，且对于 $\forall i \in [1, m]$ ，有 $a_{i} \neq a_{m - i + 1}$ ，则将其称为反回文串。现在有一个由 $n$ 个小写拉丁字母构成的字串 $s$ ，且 $n$ 为偶数。要求想用 $s$ 的一些排列构成一些反回文串 $t$ 。同时他称 $i$ 的美丽值为 $b_{i}$ ，且字串 $t$ 的美丽值 $A n s = \sum_{i = 1}^{s t r l e n (s)} b_{i} [s_{i} = t_{i}]$ ，请确定 $A n s$ 的最大值。

思路：一眼费用流，不过没想到可以直接暴力建边。

暴力建边就是建3层边，第一层是每个字符，第二层是二元组 $(x, c)$ 表示字符 $c$ 放在位置 $x$ ，第三层表示字符串的位置如果对上了的权值。直接跑最大费用最大流就行了。

1|12CF1288F Red-Blue Graph

题意：有一张二分图，左边有 $n_{1}$ 个点，右边有 $n_{2}$ 个点， $m$ 条边。每个点可能有一种颜色 R 或者 B，也可能没有，也就是 U。现在要给一些边染色，把边染成 R 要花费 $r$ 的代价，把边染成 B 要花费 $b$ 的代价，要求对于每个颜色为 R 的点，与之相邻的边中 R 的边严格多于 B 的边；对于每个颜色为 B 的点，与之相邻的边中 B 的边严格多于 R 的边。求花费最小的方案，输出任意一种，无解输出 $- 1$ 。其中 $1 \leq n_{1}, n_{2}, m, r, b \leq 200$ 。

思路：一眼流题，但是没想到竟是没写过的有源汇上下界费用流。

对于左边点，如果是R，那么由 $S$ 连下界为1的边；如果是 $B$ ，那么连向 $T$ 下界是1的边；如果是 $U$ ，由 $S$ 、向 $T$ 连下界是0的边；对于右边点同理。

最后连边 $(u, v, 0, 1, r), (v, u, 0, 1, b)$ 即可。

1|13CF1572D Bridge Club

题意：有 $2^{n}$ 个点从 $0$ 到 $2^{n} - 1$ 编号，每个点有点权，两个编号为 $u, v$ 的点之间有边当且仅当 $u$ 和 $v$ 有且仅有一个二进制位不相同。要求从这个图中选一个最多 $k$ 条边的匹配，使得被匹配所包含的 $2 k$ 个点点权和最大，输出这个最大点权和。

思路：牛逼题。

首先，容易发现是一个二分图，于是可以直接费用流。 $2 \times 10^{6}$ 的点， $2 \times 10^{7}$ 的边跑锤子啊。

正解就是发现 $k$ 很小，于是想办法优化边数。然后就惊奇的发现，每减少一条边最多会减少 $2 n - 1$ 个匹配，于是选边权最大的 $k (2 n - 1)$ 条边就行了。

trick：每减少一条边最多会减少 $2 n - 1$ 个匹配。

1|14P3227 [HNOI2013] 切糕

思路：自己只想到了建满边的做法，不知道能不能跑过去。

正确的建边方法是建若干条链。具体地，对于每个 $(x, y, z)$ ，建边 $(x, y, z) \leftarrow (x, y, z + 1)$ 边权 $v [x] [y] [z]$ ，然后考虑 D 的限制，那么就需要建边 $(x, y, z) \leftarrow (z \pm 1, y, z - d)$ 、 $(x, y, z) \leftarrow (x, y \pm 1, z - d)$ 边权为 inf，这样就可以保证相邻的链割掉的边距离不超过 D，然后跑最小割即可。

证明有点复杂，看不懂。

1|15P4298 [CTSC2008] 祭祀

题意：求 DAG 最长反链，求出一组解，判断每个点是否可能存在于最长反链上。

思路：好题。普及了很多之前不知道的和网络流相关的知识点（主要在构造方面）。

这一题要求出 DAG 最长反链，然后构造方案，并求出每个点是否可以在最长反链中。

首先，根据 $Dilworth$ 定理，偏序集最长反链等于最小链覆盖，于是求出 DAG 的传递闭包转成偏序集，然后就要求最小链覆盖。最小链覆盖的经典做法就是把一个点拆成两个点，相当于是一条长为 1 的链，然后不断合并，最后的链数就是最小链覆盖。合并的过程就是二分图匹配的过程，那么答案就是点数减去最大匹配。

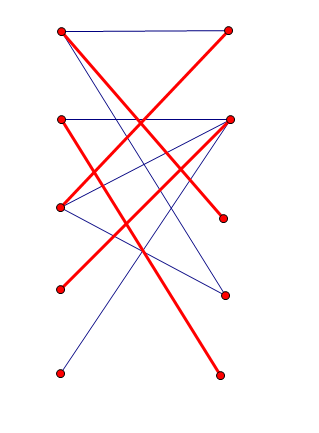
然后考虑怎么构造最长反链。首先考虑怎么构造二分图最大独立集。假设我们已经求出了最大匹配：

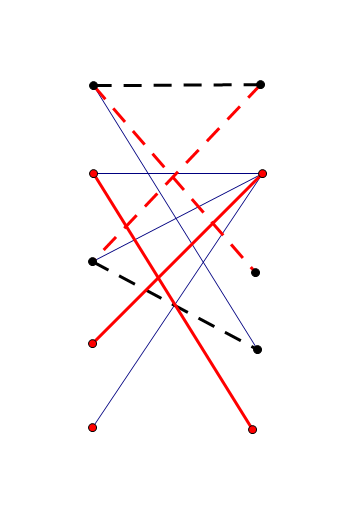
然后我们从右侧的未匹配点出发，每次只走非匹配边到左侧，只走匹配边到右侧，然后选取左边被走到的点和右边未被走到的点，发现这些点就是最小点覆盖：

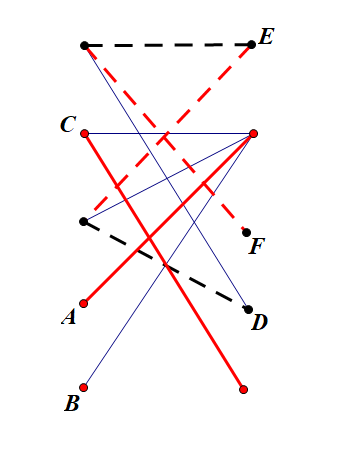
而最大独立集就是最小点覆盖的补集，于是左边未被走到的点和右边被走到的点就是最大独立集：

回到原题，可以证明一个点拆成的两个点如果都在最大独立集里那么这个点在最长反链上，于是可以求出第二问。

然后是第三问，删掉一个点和其相连的点后，如果最长反链只减小了 1 就表示这个点能在最长反链中。

1|16[ABC225G] X

题意：给定一个矩阵，你可以选定一些格子，得到这些格子的权值，但是你需要在这些格子中画 X，即连接两条对角线，但是对于格子 $(i, j)$ 和 $(i + 1, j + 1)$ ，倘若均需画线，你可以从 $(i, j)$ 的左上角直接画到 $(i + 1, j + 1)$ 的右下角，这算做一次画线，你的得分即为选定格子的权值和减去画线次数乘画线代价。

思路：因为是选或不选，考虑用最小割建模，即用总和减去最小割。那么要最小化不选的权值和画线的代价。

首先源点向每个点连 $a_{i, j}$ 的贡献，表示如果不选的代价。

对于一条连续选择的斜线，代价只用加在一处，于是可以把每个点向斜线前一项连一条容量为 $C$ 的边，如果不存在就是向汇点连边，这样代价就加在断开处，只会被算一次。

1|17CF793G Oleg and chess

题意：有一个 $n \times n$ 的矩阵，每行每列至多能放一个棋子，另外有 $q$ 个矩形的区域不能放棋子（这些矩形区域互不相交），问最多能放多少个棋子。

思路：线段树优化建边 + 网络流。

在这个限制下，每列的范围是若干区间，可以考虑用扫描线，然后新建点向这一列连边来优化建边，点数大概是 $O (n \log n)$ 的，然后跑网络流即可。

1|18P1963 [NOI2009] 变换序列

题意：给定 $i, a_{i}$ 的距离，求字典序最小的 $a_{i}$ 。

思路：可以把 $i$ 和可行的 $a_{i}$ 连边，那么我们要求的就是字典序最小的完美匹配，可以直接用匈牙利算法来解决。

在此题中，每个点左部点最多连两条边，所以直接倒着匹配就是字典序最小的方案。

1|19P2805 [NOI2009] 植物大战僵尸

题意：给定一个 $n$ 行 $m$ 列的图，每个点可以保护一些点，每个点有一个权值，如果要选择一个点的权值必须选择保护它的点和它右边的点，求最大权值。

思路：容易发现这就是最大权闭合子图的模型。最大权闭合子图是每个点有权值，如果要选择一个点就要选择这个点的所有出边，要求最大权值。

做法是对于每个点，如果权值非负，就由源点向这个点连边，否则就向汇点连边，边权就是点权的绝对值，然后对于原图中的边 $(u, v)$ ，连 $u \leftarrow v$ 的边，边权是 $i n f$ ，然后跑最小割，答案就是正点权和减去最小割。

为什么这样做是对的呢？首先，能被割掉的边一定是连向原点或者汇点的边，那么考虑与 $S$ 联通的集合 $X$ 和与 $T$ 联通的集合 $Y$ ，我们选择的点就是在 $X$ 中的点。对于一个正权点，如果划分到了 $Y$ 集合，就要付出 $v a l$ 的代价，而不选择相当于是去掉原来加上的代价；对于一个负权点，如果划分到了 $X$ 集合，那么代价是 $| v a l |$ ，相当于是加上原先负的代价。同时我们选择的点集 $X, Y$ 中也不会有连边，相当于是选择了 $X$ 中点的导出子图，于是这样做是对的。

回到这题，我们发现几乎是一样的，但是问题在于可能会出现环，于是可以建反图跑拓扑排序来去掉环的影响。

1|20CF1666K Kingdom Partition

题意：有一张图，你需要把点划分成 ABC 共 3 个部分，对于每条边，记边权为 $w$ ，代价如下：

如果连接两个 A 部分的点，代价是 $2 w$
如果连接两个 B 部分的点，代价是 $2 w$
如果连接 AC 两个部分的点，代价是 $w$
如果连接 BC 两个部分的点，代价是 $w$
求最小代价。

思路：一眼最小割模型，但是因为有 3 个部分不好建模。

我们把代价画出来，发现十分对称：

\begin{matrix} A & B & C \\ A & 2 & 0 & 1 \\ B & 0 & 2 & 1 \\ C & 1 & 1 & 0 \end{matrix}

我们考虑把每个点 $i$ 拆成 $p_{i}, q_{i}$ 两个，不然不好割成 3 个集合，然后连边 $(p_{x}, q_{y}, w), (q_{x}, p_{y}, w)$ ，设 XY 表示最后 $p_{i}$ 划分到 X， $q_{i}$ 划分到 Y，有：

\begin{matrix} S T & T S & S S & T T \\ S T & 2 & 0 & 1 & 1 \\ T S & 0 & 2 & 1 & 1 \\ S S & 1 & 1 & 0 & 2 \\ T T & 1 & 1 & 2 & 0 \end{matrix}

这时我们发现 ST 与 A 划分的代价相同，TS 与 B 划分代价相同，SS、TT 划分代价与 C 相同，这样就可以直接跑最小割来解决了。

1|21P8501 [NOI2022] 二次整数规划问题

题意：求一个序列 $x$ ，要求满足以下条件：

每个位置有限制 $[l_{i}, r_{i}]$ ，其中 $1 \leq l_{i} \leq r_{i} \leq k$ 。
有若干个限制，表示 $| x_{i} - x_{j} | \leq d$ 。

同时给出长为 $k - 2$ 的序列 $v_{2} \dots c_{k - 1}$ ，记 $G$ 为满足 $| x_{i} - x_{j} | \leq 1$ 的二元组 $(i, j)$ 个数，记 $c_{i}$ 表示 $x_{j} = i$ 的数量，那么权值定义为 $10^{6} G + \sum c_{i} v_{i}$ ，求满足条件的序列的权值最大值。

思路：绝世好题。

就从部分分开始吧。

1|0k=3

发现一个性质，就是如果一个元素的取值不固定，那么一定取 2 最优。

证明比较简单，因为把一个元素变成 2 不会影响第二类限制是否满足，而且这样不会让 $c_{2}$ 和 G 减小，那么就不会更劣。

于是就可以在 $O (n + m + q)$ 的时间里解决 $k = 3$ 。

1|0k=4

考虑能否延用 $k = 3$ 的做法。

这时有一个结论，对于任意的 $k$ 和非负 $k - 2$ 元组 $(c_{2}, c_{3}, \dots, c_{k - 1})$ ，每个非必须取 $1$ 和 $k$ 的元素取 $[2, k - 1]$ 一定不劣。

证明和上一个证明类似。

于是这时就只需判断每个元素是取 2 还是取 3。这时它们之间对 G 的贡献是一定的，于是每个数取 2 和取 3 对答案的贡献是线性的，于是一定是全取 2 或者全取 3 更优。

不过在确定每个元素的取值范围是要注意必须取 1 和 $k$ 的元素对其他元素的影响，可以用差分约束来求出每个元素最终的取值范围。

1|0特殊性质 A

因为选的数之间没有限制，因此需要考虑的取值范围只有 $[2, 3], [2, 4], [3, 4]$ 。

此时有结论，对于取值范围相同的元素，它们都取同一个数是最优的。于是只有 $2 \times 2 \times 3 = 12$ 种情况，直接计算即可。

复杂度 $O (n + m + q)$ ;

1|0特殊性质 B

这时可以考虑暴力枚举每个被限制的元素的取值，考虑在有限制的变量之间连边，那么对于每个连通块， $c_{2} + c_{3} + c_{4}$ 是定值，于是可以用一个二元组 $(c_{2}, c_{4})$ 来描述，可以在 $O (3^{m} m)$ 的时间内求出所有合法的 $O (m^{2})$ 个二元组。没有限制的元素可以像特殊性质 A 一样处理。

复杂度 $O (n + 3^{m} m + q m^{2})$ 。

1|0∑q 较小

我们可以把对 $G$ 的贡献看成每一对二元组之间一个选 2 一个选 4 会有 $10^{6}$ 的贡献，不满足限制的代价是 $\infty$ ，就相当于是两个元素差值大于 $b_{j}$ 就产生一定代价，发现这很像 [HNOI2013] 切糕的建模，于是可以直接用最小割。

1|0特殊性质 C

通过上一个做法，我们不难想到可以求出所有可能作为最优解的二元组 $(c_{2}, c_{4})$ ，于是可以用随机化。我们随机 $v_{2}, v_{3}, v_{4}$ 的取值，然后计算出最优的 $(c_{2}, c_{4})$ ，大概随 500 次左右就没问题。

1|0对于 100% 的数据

从特殊性质 C 我们不难发现，我们只关心哪些二元组 $(c_{2}, c_{4})$ 能取到最优解，其他的都不重要。

我们先把答案写成只有 $c_{2}, c_{4}$ 的样子。为了避免出现 $n$ ，我们不直接求答案，而是求 $(c_{2}, c_{4})$ 相对于 $(0, 0)$ 增量： $c_{2} (v_{2} - v_{3} + 2 \times 10^{6} c_{1}) + c_{4} (v_{4} - v_{3} + 2 \times 10^{6} c_{5}) - 2 \times 10^{6} c_{2} c_{4}$ ，可以写成 $- 2 \times 10^{6} (c_{2} - C_{1}) (c_{4} - C_{2}) + C_{3}$ ，于是就要最小化 $(c_{2} - C_{1}) (c_{4} - C_{2})$ 。

我们把二元组 $(c_{2}, c_{4})$ 放到平面上，设 $min c_{2}$ 为 $c_{2}$ 的最小值，那么我们一定可以取到 $(min c_{2}, min c_{4}), (min c_{2}, max c_{4}), (max c_{2}, min c_{4})$ ，同时所有点都在 $([min c_{2}, max c_{2}], [min c_{4}, max c_{4}])$ 内，这样求 $(c_{2} - C_{1}) (c_{4} - C_{2})$ 的最小值就相当于是把所有 $(c_{2}, c_{4})$ 平移后取横纵坐标乘积的最小值。

这时已经确定了的有左下、左上、右下 3 个点，于是只要矩形最后不是全部落在第三象限，取这 3 个点都最优，于是只用考虑矩形全部在第三象限的情况。

因为是坐标乘积最小，不难想到凸包，那么我们就需要求出凸包上的所有点，于是可以用 [BalkanOI2011] timeismoney | 最小乘积生成树的做法——分治求凸包上的点。具体地，假设当前要找到在 $(x_{1}, y_{1}), (x_{2}, y_{2})$ 间的凸包，那么就是要找到一个点 $(x, y)$ 满足 $(x_{1} - x_{2}, y_{1} - y_{2})$ 和 $(x, y)$ 的叉积最大，如果 $(x, y)$ 不在线段 $(x_{1}, y_{1}, x_{2}, y_{2})$ 上，那么其就是一个新的在凸包上的点，可以向两边递归下去。

那么问题就是每个元素取 2 有 $y_{1} - y_{2}$ 的贡献，取 4 有 $x_{2} - x_{1}$ 的贡献，要让总贡献最大。我们可以先都加上 $y_{1} - y_{2} + x_{2} - x_{1}$ ，于是取 2 有 $x_{2} - x_{1}$ 的代价，取 4 有 $y_{1} - y_{2}$ 的代价，取 3 有 $y_{1} - y_{2} + x_{2} - x_{1}$ ，要求最小代价。这时有影响的限制就是 $| x_{p_{j}} - x_{q_{j}} | \leq 1$ ，即这两个元素不能一个选 2 一个选 4。

于是考虑建立最小割模型。我们把每个元素拆成 2 个点 $p 1_{i}, p 2_{i}$ ，然后钦定割掉 $S \to p 1_{i}, p 1_{i} \to p 2_{i}, p 2_{i} \to T$ 分别代表取 2、3、4，那么每个限制就可以连边 $p 2_{i} \overset{\infty}{\to} p 1_{j}, p 1_{i} \overset{\infty}{\to} p 2_{j}$ 。这样我们跑一遍最小割就可以求出最优的 $(c_{2}, c_{4})$ 。

__EOF__

本文作者：Xttttr
本文链接：https://www.cnblogs.com/Xttttr/p/17391970.html
关于博主：评论和私信会在第一时间回复。或者直接私信我。
版权声明：本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【推荐】一下。您的鼓励是博主的最大动力！

posted @ 2023-05-11 19:14 Xttttr 阅读(38) 评论(0) 编辑收藏举报

刷新页面返回顶部

登录后才能查看或发表评论，立即登录或者逛逛博客园首页

相关博文：

· NOI真题记录

· 网络流24题做题记录

· 网络流与各种建模（I）

· 网络流与图匹配

· 二分图与网络流，ACMer需要掌握的一些模型

阅读排行：
· 地球OL攻略 —— 某应届生求职总结
· 周边上新：园子的第一款马克杯温暖上架
· Open-Sora 2.0 重磅开源！
· 提示词工程——AI应用必不可少的技术
· .NET周刊【3月第1期 2025-03-02】

公告

网络流做题记录

发表于 2023-05-11 19:14阅读：38评论：0推荐：0

做题记录

关注

跳至底部

昵称： Xttttr
园龄： 2年6个月
粉丝： 11
关注： 95

+加关注

随笔档案

阅读排行榜

评论排行榜

1. 2023中山纪中八校集训(1)

Xttttr

网络流做题记录

1|0网络流做题记录

1|1P4126 [AHOI2009]最小割

1|2P3731 [HAOI2017]新型城市化

1|3P5331 [SNOI2019]通信

1|4P5192 Zoj3229 Shoot the Bullet|东方文花帖|【模板】有源汇上下界最大流

1|0无源汇上下界可行流

1|0有源汇上下界可行流

1|0有源汇上下界最大流

1|5P4843 清理雪道

1|0有源汇上下界最小流

1|6P4043 [AHOI2014/JSOI2014]支线剧情

1|0有源汇上下界费用流

1|7P4553 80人环游世界

1|8CF277E Binary Tree on Plane

1|9P5030 长脖子鹿放置

1|10P4412 [SHOI2004] 最小生成树

1|11CF884F Anti-Palindromize

1|12CF1288F Red-Blue Graph

1|13CF1572D Bridge Club

1|14P3227 [HNOI2013] 切糕

1|15P4298 [CTSC2008] 祭祀

1|16[ABC225G] X

1|17CF793G Oleg and chess

1|18P1963 [NOI2009] 变换序列

1|19P2805 [NOI2009] 植物大战僵尸

1|20CF1666K Kingdom Partition

1|21P8501 [NOI2022] 二次整数规划问题

1|0k=3

1|0k=4

1|0特殊性质 A

1|0特殊性质 B

1|0∑q 较小

1|0特殊性质 C

1|0对于 100% 的数据

公告

Xttttr

网络流做题记录

搜索

常用链接

我的标签

随笔档案

相册

阅读排行榜

评论排行榜

推荐排行榜

最新评论