神经网络后馈算法剖析

在coursera中Ng的机器学习课程中，他介绍了神经网络中的前向传播算法以及后馈算法，但是对于后馈算法中，为什么要那么做，只用了一句需要使用复杂的数学来证明。我查阅了相关的资料，对这一部分的原理进行了学习，现将这部分知识记录下来，以供共同学习。

1、简单的线性模型中误差分析

使用一个大小为N的训练集对一个预测（分类）模型进行训练时，总误差为：

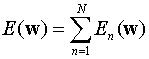  　　　　　　 ————（1）

而在一个线性模型中，第k个输出y_k是输入x_i的线性组合：

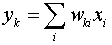　　　                  　　————（2）

其中，w_ki是第i个输入到第k个输出的边权。对于某个输入数据（另外一种讲法叫模式）n，它的误差函数被定义为：

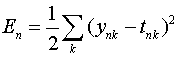　　　 　　————（3）

其中，y_nk为：

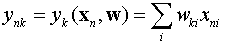　　————（4）

t_nk是输入数据n是先所打上的标签，即真实结果。

由（3）和（4）可求得：

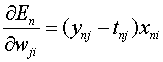　　   　　　  ————（5）

我们可以看到，误差对某个边权w_ji的偏导，等于这个边所连输出端的误差信号（y_nj-t_nj）与这个边所连输入端的变量的乘积。

2、神经网络的后馈算法

2.1 前馈过程

一个简单的神经网络模型如下图所示：

这个神经网络有1个输入层，2个隐层以及1个输出层；对于某个unit（神经元），它的输入等于各个前一层神经元的加权和：

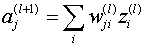　         　　　　————（6）

其中，带括号的上标表示层数，（6）也可以写成向量的形式：

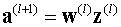　　　　                　————（7）

经过每个神经元activation函数h()的处理后，第l层第j个神经元的输出为：

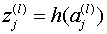　　　                    　　————（8）

需要注意的是，我们可以在每一层中，加入一个修正神经元，它的activation输出始终是+1。神经网络不断地重复（6）、（8），直到输出层产生相应的输出，神经网络的输出层神经元直接将输入加权作为结果输出，而不经过h()的处理。这是神经网络的前馈过程。

2.2 后馈过程

现在我们考虑后馈的过程，E_n对w_ji的偏导只通过输入a_i传导到神经元j，应用偏导的链式法则有：

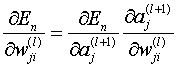　　　   　　————（9）

我们定义：

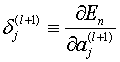　　　　　                 ————（10）

它表示(l+1)层神经元j的误差。而：

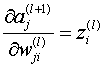　　　　                     　————（11）

将（10）、（11）代入（9），可得：

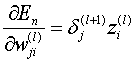　　　　　             ————（12）

（12）说明在神经网络中，误差对l层某个边权w_ji的偏导，等于这个边所连输出端（l+1层第j个神经元）的误差与这个边所连输入端（l层第i个神经元的输出）的乘积。（12）写成向量的形式为：

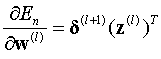　　　        　　————（13）

这个就是最终的结论！

2.3 误差的后馈传播

下面介绍如何计算。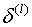

 

在输出层中，有：

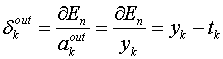　　　 ————（14）

而对于隐层或者输入层，有：

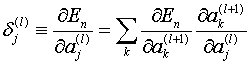　   ————（15）

（15）式实际上表示了一个误差后馈的过程，l层的误差是l+1层的误差通过w^(l)传递过来的。由于：

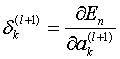　　                      　　　————（16）

由（6）、（7）式可得：

　　　　          　————（17）

（16）、（17）代入（15）可以得到：

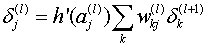　　　　　————（18）

（18）写成向量的形式为：

                                                                                            　　　　　　————（19）

其中.*表示点乘。

 

2.3 误差后馈总结

1. 将一个输入向量x_n输入到网络中，使用公式（6）、（8）前向转播；
2. 使用（14）式计算输出层的误差δ；
3. 后馈输出层的δ，并计算每一个隐层的δ。
4. 使用（13）计算所求的偏导。