# POJ1201_Intervals

题意：

---

有n个闭区间形如[ai, bi]，每个区间还附有一个数ci，

要求你构造一个整数集合Z，使得对于每一个区间，至少有ci个数x满足ai<=x<=bi

问：这样的整数集最少有几个数？

解：

---

因为0<=ai,bi<=50000

所以题意其实为从[0, 50000]中选出若干整数，使[ai, bi]区间中至少有ci个数被选

设s[k]表示从[0, k]之间选了几个数

显然有n个约束s[bi]-s[ai-1]>=ci

但是，只有这样的约束依然无法求出有意义的解，必须添加适当的隐性条件：

1、s[k]-s[k-1]>=0

2、s[k]-s[k-1]<=1 ===> s[k-1]-s[k]>=-1

k从0枚举到50000

然后因为最小的点为-1，所以以-1为起点求最长路，dis[50000]即s[50000]为答案

---

*为什么隐性条件至关重要？如图

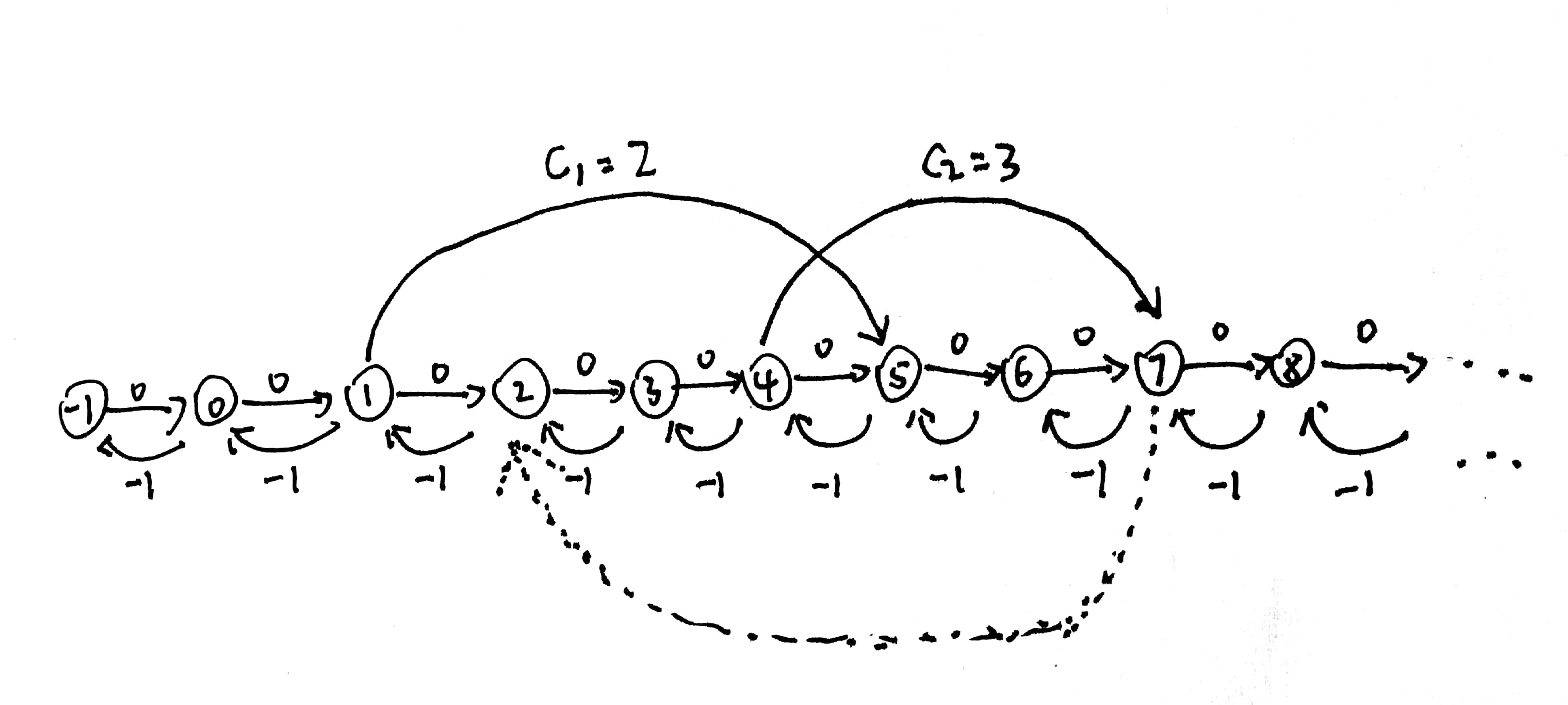
0<=s[k]-s[k-1]<=1的两个条件使得节点之间连成了可以向前也可以向后的链

其实可以发现，s[bi]-s[ai-1]>=ci只是连接了几个散点，如果没有两个隐形条件，图将不连通，最长路将无法开始

同时，缺少了0和-1这两种边中任意一种，也必将导致答案不正确

例如图上构造的数据

[a1 = 2, b1 = 5] c1 = 2
[a2 = 5, b2 = 7] c2 = 3

若没有0边，显然，-1点与其他点根本不可达

若没有往回走的-1边，最长路会求得为3，而正确答案为4

不要强行将极其抽象的东西进行解释，就如此题，纠结最长路在图上的求解过程具体对应什么含义是不可取的

我们只用知道少构造了边，就会导致答案错误，这就足够了

*为什么不会出现正环？

————图上的虚线边是一个例子，只有从后面的节点指向前面的节点，并且边权为正才会出现正环

而当7指向2时，ai=8，bi=2，此时bi-ai+1=-5，按照题意，ci应<=-5

但是题目又说ci>=1，矛盾，所以不存在这种情况，不存在正环

*为什么不用更多的隐性条件？比如0<=s[k]-s[k-2]<=2？

————你会发现，k->k-2一条长-2的边与k->k-1->k-2每边-1完全等价

多加各种边只会浪费时间，对答案不会有任何贡献

代码：

---

上文分析过，-1应该是最小的节点，所以从-1开始跑最长路

但是除非开map，否则我们不能实现head[-1]...的存储

经过分析，其实从0点开始遍历对结果无影响，所以代码与上文微有不同

代码实现也是艺术啊

#include <bits/stdc++.h>
using namespace std;
const int N = 50010;
int n;
int head[N], nxt[N << 2], edge[N << 2], ver[N << 2], tot;

void add(int u, int v, int w) {
    ver[++tot] = v; edge[tot] = w;
    nxt[tot] = head[u]; head[u] = tot;
}

struct node{
    int w; int num;
};
bool vis[N];
int dis[N];
void f_spfa() {
    queue<int> q;
    memset(dis, -0x3f, sizeof dis);
    dis[0] = 0;
    q.push(0);
    vis[0] = true;
    while (!q.empty()) {
        int x = q.front(); q.pop();
        vis[x] = false;
        for (int i = head[x]; i; i = nxt[i]) {
            int y = ver[i]; int z = edge[i];
            if (dis[y] < dis[x] + z) {
                dis[y] = dis[x] + z;
                if (!vis[y]) 
                    vis[y] = true, q.push(y);
            }
        }
    }
    return;
}
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int ai, bi, ci;
        scanf("%d%d%d", &ai, &bi, &ci);
        add(ai - 1, bi, ci);
    }
    for (int i = 1; i <= 50000; i++) {
        add(i, i - 1, -1);
        add(i - 1, i, 0);
    }
    // f_dij();
    f_spfa();
    printf("%d\n", dis[50000]);
}

dijkstra算法不能求单源最长路，将最长路边权取反，然后跑单源最短路可以达到相同效果

因为最长路时每个节点不止更新一次，所以只有spfa能跑最长路