Topology and Geometry Seminar

 

Slides: https://github.com/CubicBear/GeoTop

Here are the slides of the seminars about topology and geometry. The topics are selected to be more relative to representation theory (but it, unfortunately, ended in the middle so the representation part has no chance to be reflected). But anyway, I thought this would be an introductory resource to the geometry of fiber bundles. 

• Spectral Sequences (I)
• Spectral Sequence (II)
• Characteristic Classes (I)
• Characteristic Classes (II)
• K-theory (I)
• K-theory (II)
• Computation

---

 

• Equivariant Version (I)
• Equivariant Version (II)
• Sheaf theory (I)
• Sheaf theory (II)
• Intersection Homology and Perverse sheaves (I)
• Intersection Homology and Perverse sheaves (II)
• $\mathcal{D}$-modules (I)
• $\mathcal{D}$-modules (II)

Tips: the lectures with (I) are more important than the one with (II). 

Appendix: the topics in the plan and in the imagination. 

---

 

Lecture 1 to Lecture 7

Time: each Friday, 

> 20:00-21:30, chat from 19:30 (Beijing, UTC+8) 

> 15:00-16:30, chat from 14:30 (Moscow, UTC+3) 

Tencent Meeting: 765 3760 2473 (QR code)

 

Lecture 1 Spectral Sequences (I)

Slide: (TopGeo)Lecture1.pdf 

Date: 2020/9/18 

Introduction
Filtered complexes
Leray-Serre Spectral Sequences
Applications

The reflection of the first lecture is not that good, so I plan to change a little the style of lecturing. 

Lecture 2 Spectral Sequences (II)

Slide: (TopGeo)Lecture2(1).pdf 

 

Date: 2020/09/25 19:30-21:30 (Beijing, UTC+8) 14:30-16:30 (Moscow, UTC+3) 

Remind
Double complexes
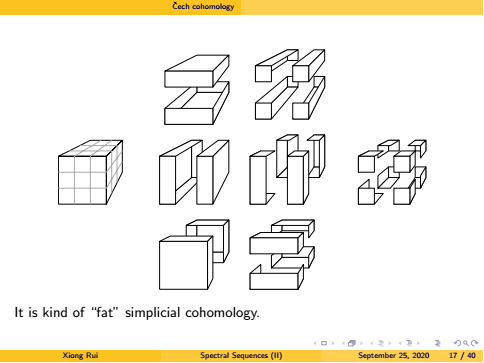
\v{C}ech cohomology
Grothendieck Spectral Sequences
Applications

Maybe this time is better. Purely reading the slide makes perfect. 

Lecture 3 Characteristic Classes (I) 

Slide: (TopGeo)Lecture3(3).pdf

 

Date: 2020/10/02

Vector Bundles
Classifying Vector Bundles
Chern Classes

There is some possibility that next time, some of the proof details will be omitted. 

Lecture 4 Characteristic Classes (II)

Slide: (TopGeo)Lecture4(3).pdf

Date: 2020/10/09

I will also simultaneously make one on skype if there will be some foreigners (I suggest to write to me if you are)

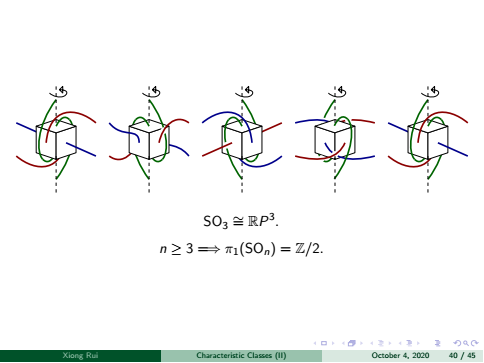
Axioms of Chern Classes
Chern Classes in Differential Geomtry
Chern Classes in Algebraic Geometry
General Characteristic Classes
Vector Bundles over Spheres

There is some problem with the slide, which is described at the beginning of the uploaded one. I will make a new one later. (It is uploaded)

Lecture 5 K-theory (I)

Slides: (TopGeo)Lecture5(2).pdf

Date: 2020/10/16

Definitions
Bott Periodicity
Chern Character
Thom isomorphisms
Atiyah--Hirzebruch Spectral Sequences

 

Lecture 6 K-theory (II)

Slide: (TopGeo)Lecture6.pdf 

Date: 2020/10/23

K in Algebra
K in Analysis
K in Algebraic Geometry
Higher K

 

Lecture 7 Computations

Slides: (TopGeo)Lecture7(2).pdf

Date: 2020/10/30

Trivial Bundles
Spheres
Projective Spaces
Determinant
Curves
Classifying Spaces
Flag Manifolds
Grassmannians
Classifying Spaces
Flag Manifolds
Grassmannians

In this lecture, the role of the spectral sequence is reflected. 

References

Note that the separated references are given at the end of each slide. Here are some general references. 

Benson. Cohomology and Representation, second volume.
May. A Concise Course in Algebraic Topology. 
Bott, Tu. Differential Forms in Algebraic Topology. GTM82. 
Broden. Topology and Geometry. GTM129. 
Husemoller. Fibre Bundles.GTM20. 
Fomenko, Fuchs. Homotopy Topology. GTM273. 
Milnor, Stasheff. Characteristic classes. 
Atiyah. K theory.

The first 7 lectures above are the basic part of our seminar. The lectures later will be more introductory with less proof. 

 

News: no more. It finished. 

 

---

Lecture 8 Equivariant Version (I)

Slides: (TopGeo)Lecture8(2).pdf

Record: Equivariant Version (I)

Date: 2020/11/14

Time: 18:00-20:00 (Beijing, UTC+8) 13:00-15:00, chat from 14:30 (Moscow, UTC+3) 

Tencent Meeting: 457 796 895 (QR code)

Equivariant Cohomology
Spectral Sequences
Fundamental Classes
Other Forms
Equivariant K-theory
Other forms

Ref: 

Goresky, Kottwitz, and Macpherson. Equivariant cohomology, Koszul duality, and the localization theorem.

Xiong. Comodule Structures, Equivariant Hopf Structures, and Generalized Schubert Polynomials. [arXiv] 

Fulton. Young Tableaux with Application in Algebra and Geometry. 

Guillemin, Sternberg, Brüning, Supersymmetry, and Equivariant de Rham Theory.

Deligne. Théorie de Hodge, III. 

Bernstein and Lunts. Equivariant sheaves and functors. 

Segal. Equivariant K-theory. 

Atiyah. Equivalent K theory and Completion. 

Chriss, Ginzburg. Representation Theory and Complex Geometry.

Lecture 9 Equivariant Version (II)

Slides: (TopGeo)Lecture9.pdf

Record: Equivariant Version (II) (it sucks)

 

Fixed Points and Tori
Localization Theorem (I)
Localization Theorem (II)
Localization Theorem (III)
Localization Theorem (IV)
Localization Theorem (V) 

Ref: 

Milne. Algebraic Groups.

Hsiang. Cohomology Theory of Topological Transformation Groups.

Chriss, Ginzburg. Representation Theory and Complex Geometry. (essentially, Thom's papers)

Goresky, Kottwitz, and MacPherson. Equivariant cohomology, Koszul duality, and the localization theorem.

Jantzen. Moment graphs and representations.

Kaji. Three presentations of torus equivariant cohomology of flag manifolds. [arXiv] 

Lecture 10 Sheaf Theory (I)

Slides: (TopGeo)Lecture10(2).pdf (also Github)

Time: Nov 28th, 18:00-21:00 (Beijing, UTC+8)

Tencent Meeting: 615 4671 9597

Sheaves
Morphisms
Examples
Functors
Examples

No references 

Lecture 11 Sheaf Theory (II)

Slides: (TopGeo)Lecture11(2).pdf (also Github)

Time: 2020/12/4 19:00-22:00

Tencent Meeting: 986 409 538

Homological Algebra
Realization of Topology (I)
Homological Algebra (II)
Realization of Topology (II)

References: 

Verdier. Dualité dans la cohomologie des espaces localement compacts. [pdf]

Borel, Moore. Homology theory for locally compact spaces. [pdf]

Lecture 12 Intersection Homology and Perverse Sheaves (I)

Kirwan, Woolf, An introduction to intersection homology.

Goresky, MacPherson. Intersection homology I. [pdf]

Brasselet. A walk in the world of perverse sheaves. Lecture 1 [Youtube], Lecture 2 [Youtube], Lecture 3 [Youtube]. 

Lecture 13 Intersection Homology and Perverse Sheaves (II)

Goresky, MacPherson. Intersection homology II. [pdf]

MacPherson. Intersection cohomology and Perverse Sheaves. [pdf]

Ginzburg. Geometric methods in the representation theory of Hecke algebras and quantum groups. [arXiv]

Hotta, Takeuchi, Tanisaki. D-Modules, Perverse Sheaves, and Representation Theory. 

Etingof. Introduction to Algebraic $\mathcal{D}$-module. [pdf]

Kirwan, Woolf, An introduction to intersection homology. 

Lecture 14 $\mathcal{D}$-modules (I)

Lecture 15 $\mathcal{D}$-modules (II)

See my note: DModules.pdf

---

 

Gallary