乘积和对偶
之前写过一篇『映射的度』,虽然现在看还是有点naive,不过我觉得这种形式不错。
代数拓扑中各式各样的乘积眼花缭乱,叉积,cup积,cap积,相交积。关于对偶的表述也随着乘积变得清晰。下面我们就来从各个角度介绍这件事。
目录
综述
对于拓扑空间$X$,记$C(X)$为奇异链复形。
对于拓扑空间$X,Y$,Eilenberg–Zilber 定理断言存在一对映射
$$P: C(X)\otimes C(Y) \to C(X\times Y)\qquad Q: C(X\times Y)\to C(X)\otimes_R C(Y),$$
使得他们给出两个链复形的同伦。具体的构造通常很有用,它们被称为Eilenberg–Mac Lane映射和Alexander–Whitney映射。于是我们可以定义
- 外积。$H^*(X)\times H^*(Y)\to H^*(X\times Y)$。由$C(X,Y)\to C(X)\otimes C(Y)$反变诱导。
- Cup积。$H^*(X)\times H^*(X)\to H^*(X)$。由对角映射$C(X)\stackrel{\Delta}\to C(X\times C)\to C(X)\otimes C(X)$反变诱导。
- Cap积。$H^*(X)\times H_*(X)\to H_*(X)$。由$\operatorname{Hom}(C(X),\mathbb{Z})\otimes C(X)\stackrel{\Delta}\to \operatorname{Hom}(C(X),\mathbb{Z})\otimes C(X)\otimes C(X)\stackrel{eva}\to C(X)$诱导。
这让上同调$H^*(X)$成为一个环,下同调$H_*(X)$成为一个$H^*(X)$模。他们在连续映射下表现良好,实际上,对于连续映射$f: X\to Y$,这诱导了环同态$f^*:H^*(Y)\to H^*(X)$,且诱导了$H^*(Y)$-模同态$f_*: H_*(X)\to H_*(Y)$,即满足投射公式
$$f_*(f^*(y)\cap x)=y\cap f_*(x)$$
其中$y\in H^*(Y)$,$x\in H_*(X)$. 具体的讨论可见[3](9.7.1), [2], [1].
以代数拓扑观之
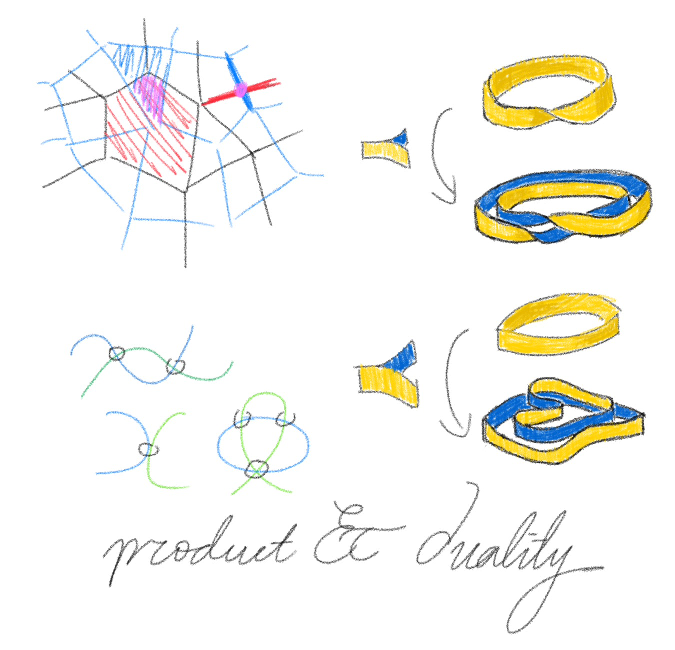
首先,撇去乘积不谈。古典的对偶定理来自一个非常经典经典的观察——对偶多面体(见第一张图)。如果有这样一个『多面体分解』,那么对应的『对偶分解』就十分有趣。如果记这个对偶是$D$,那么,例如在二维情况,
- $D(\textrm{顶点})=\textrm{面}$,
- $D(\textrm{楞})=\textrm{楞}$,
- $D(\textrm{面})=\textrm{顶点}$,
- $\textrm{顶点在楞上}\iff D(\textrm{楞})\textrm{在}D(\textrm{顶点})\textrm{上}$,
- $\textrm{楞在面上}\iff D(\textrm{面})\textrm{在}D(\textrm{楞})\textrm{上}$。
以上被带入$D$的都是多边形的组成零件。所以计算胞腔同调时边缘算子完全对偶,所以
$$H^2=H_0, \quad H^1=H_1\quad H^0=H_2. $$
这个观察自然非常美丽,但是需要我们认真考虑何时这是正确的。
- 首先对于$\mathbb{R}^2$,这就不对,这是因为取对偶时Hom把直和变成了直积。
- 其次对于闭圆盘$\mathbb{D}^2$,这也不对,因为边缘上无法严格对偶。
- 最后对于不可定向,这也不对,因为虽然拓扑意义上的边缘满足条件,但是我们不知道一条边给正号还是负号。
一个事实是,紧致n维流形必可剖分成有限n维多边形。所以Poincaré对偶定理是这样表述的
定理(Poincaré对偶)对于$n$维紧致可定向流形$M$,$H^{n-p}(M)\cong H_p(M)$.
实际上,cap积在此时非常具有几何意义,如果$x\in H^*(M)$,其对偶$D(x)$表成一个单形,$y\in H_*(M)$表成一个单形,那么$x\cap y$正是$D(x)$和$y$相交的部分(见第一张图),证明见[2] P197 1.9。既然有多边形分解,那么$M$本身就可以写成一些单形的和,记作$[M]$,成为正则元,那么这个同构根据几何意义,就是$ - \cap [M]$。这样的好处在于这样我们不必一直忙碌于寻找对偶,因为$\cap$积在连续映射的诱导下表现良好。
以上是最质朴的看法。比较现代的看法是
- 如果我们能局部证明对偶定理,那么把用Mayer–Vietoris序列粘一下,用点代数证明就可以了。不过『局部』是开的,我们需要一些修改。
- 局部能否粘起来,取决于同构的选取。既然我们知道$-\cap [M]$是这样一个同构,那么问题就是$[M]$能否粘起来。
能否整体粘起来其实就是可定向的表述。在代数拓扑中我们可以选择在每个点$x\in M$, 制作纤维$H^n(M,M\setminus x; \mathbb{Z})$,得到一个纤维丛$\Theta$. 如果考虑$\{\pm 1\}\subseteq \mathbb{Z}$这相当于把流形的两面撕开(见第二张图和第四张图)。可以证明
$$H_n(M,M\setminus A)\cong \Gamma_c(A,\Theta)$$
其中$A$是闭的,$\Gamma_c$表示紧支撑的截面(sections)组成的集合。具体细节参见[1] P340 第VI章 第7节。
以微分几何观之
换微分几何看。首先是de Rham理论断言,对于流形$M$,微分形式给出的上同调群(de Rham上同调)和奇异上同调($\mathbb{R}$系数)是一样的。且cup积和微分形式的外积相同——这是因为奇异上同调和de Rham上同调的乘积在$H^0$上是一致的。具体见[4] P212的过程和 P214 5.45的表述和前面的评注. 因为现在系数在域上,我们可以直接使用万有系数定理,得到
$$H^p(M,\mathbb{R})=H_p(M,\mathbb{R})^\vee$$
这里$\{*\}^{\vee}$表示对偶空间。
此时或许Poincaré对偶断言的同构有另一重看法。首先任何一个流形$M$都可以配一个Riemann度量。我们可以定义一个配对
$$H^p_{\rm de Rham}(M)\times H^{n-p}_{\rm de Rham}(M)\longrightarrow \mathbb{R}\qquad (\omega,\beta)\longmapsto \int_M \omega\wedge \beta. $$
这个和是有限的,如果这个流形$M$是紧致的。利用Hodge理论可以证明这是一个完美配对,从而$H^{n-p}(M)\cong (H^p)^\vee\cong H^p$. 具体细节见[4] P226 定理6.13.
如果我们记Poincaré对偶的映射是$D$,那么我们可以在同调群$H_*$上对偶于cup积定义相交积$\cdot$,其几何意义是单形的相交。我们直觉上希望对于好的情况,$X\cdot Y=\pm (X\cap Y)$,这里$X\cap Y$是集合论意义下的相交。这在微分几何中也有对应。对于曲面中的两条曲线(或者任意维数互补的两个嵌入自流形),当他们直截时,可以通过行列式定义正负决定我们要正号还是负号计算交点数目(图3是一些需要考虑的情况)。具体见 [5] P125 第3章 第15节。
以代数几何观之
最后我们用代数几何角度来看待这个问题。我们主要关注$\mathbb{C}$的情况。在代数簇(概形)上使用层的上同调(实际上在微分几何中我们也用了)是更为『一般』的考虑。有下面几个基本的定理。
Grothendieck消失定理. 如果$X$是$n$维noether拓扑空间,任意层$\mathscr{F}$,$H^{>n}(X,\mathscr{F})=0$.
定理(Serre). 如果$X$是noether拓扑空间,那么$X$仿射当且仅当$H^{>0}(X,\mathscr{F})=0$对所有拟凝聚层$\mathscr{F}$,当且仅当$H^1(X,\mathscr{F})=0$对所有拟凝聚层$\mathscr{F}$.
一种计算上同调方法是Čech上同调。回顾我们在拓扑中所作的『撕开两面』的纤维丛的最好替代就是最顶层微分形式丛$\omega_X=\bigwedge^{\operatorname{rank}} \Omega_X$. 由于代数几何的同调不是由单纯对象定义的,所以按『道理』不应该有『乘积』,也没有『下同调』。所以cap,cup积基本属于不可能了。但是我们希望能有类比,如果将cap积全部通过Poincaré对偶或者万有系数对偶过来只剩配对和上同调,再作一些类比$\mathscr{H}om(\mathscr{F},\omega_X)\times \mathscr{F}\to \omega_X$将会给出
$$\operatorname{Ext}^i(\mathscr{F},\omega_X)\times H^{n-i}(X,\omega_X)\to H^n(X,\omega_X)$$
希望这是一个完美配对,我们至少要求$H^n(X,\omega_X)=\mathbb{C}$,结果是
Serre对偶定理. 对于$\mathbb{C}$上的非奇异射影簇$X$,Cohen-Macaulay,等维数$n$,那么对所有凝聚层$\mathscr{F}$,都有
$$\operatorname{\mathscr{F},\omega_X}\cong H^{n-i}(X,\mathscr{F})^\vee. $$
或者写成
$$H^i(X,\mathscr{F})=H^{n-i}(X,\mathscr{F}^\vee \otimes\omega_X)^\vee. $$
以上内容可见[7]整个第三章。
最后还是提一下相交理论,我们想考虑两个子簇的相交,这也被视为是代数的乘积理论。
- 我们需要考虑链复形中$\ker d$的角色,应该是闭子簇/闭既约子概形。
- 因为代数簇是复的,所以出现的所有『(cycle, 类比于复形$\ker d$的元素)』其实是交换的——因为是复的,没有定向问题/因为复的,所以只有偶数维,此时分次交换性就是交换性。
- 然后我们需要一些等价关系,这被称为有理等价,粗略地说和定义同伦的方式类似。
- 建立乘法理论(相交积)。相交理论的大且基础的定理就是这样的乘法存在。
这样可以得到一个环,被称为周群(或周环)。我感到自己知识匮乏,还是多提一些历史抛砖引玉——实际上相关的问题由来已久,
- 早在18世纪,就已经有关于相交的Bezout定理;
- 19世纪Schubert做了相当多计算,不过理论基础值得怀疑;
- 20世纪伊始,这作为Hilbert 15问题被重新提出;
- 20世纪50年代,华裔数学家周炜良为我们搭建了周环的基本理论;
- 20世纪60年代,Grothendieck提出了Motive理论……
可以参见漂亮的教材[8]。
参考文献
[1] Bredon. Topology and Geometry.
[2] 姜伯驹. 同调论.
[3] Dieck. Algebraic topolog.
[4] Warner. Foundations of Differentiable Manifolds and Lie Groups
[5] Dubrovin, Fomenki, and Novikov. Modern Geormetry II. Geometry and Topology of Manifolds
[7] Hartshorne. Algebraic Geometry.
[8] Eisenbud and Harris. 3264 and All That.
后记
这些其实我一直没有搞得特别清楚,不过感觉毕业论文会大量地使用代数拓扑(或者说胞腔的那套理论),所以最近复习兼预习了一些。最早看得姜伯驹的Poincaré对偶的介绍,现在看感觉似乎太组合了……之后有机会我会再总结一篇示性类,这个目前我还蒙在鼓里。另外Bredon真的是好书——告诉你所有值得被知道的东西。
最近认识了一些兴趣相投的朋友,感觉开心。(´▽`ʃ♡ƪ)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号