[Bilingual]魔术农庄里的不变量 Invariants in Magic Farm

目录

Contents

 

 

 

近来，我在新生群里听说了这样一个有趣的问题。

Recently, I heard an interesting problem in freshmen group. 

很久以前，有三种羊，红羊，蓝羊，黄羊。

Long time ago, there were three kinds of animals, say red sheep, blue goat and yellow lamb. 

他们住在一个名为『魔术农庄』的农场。

They lived in a farm called Magic Farm.

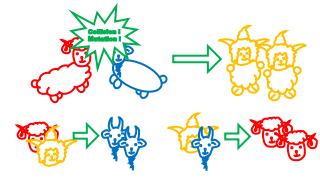如果两只不同色羊相撞，那么他们变成第三种颜色。

If two different animals collide, then they will convert into the other one species. 

有红蓝黄三色羊各15，19，20只，问最后会不会出现 所有绵羊同色的情况？

There are 15 red sheep, 19 blue goats and 20 yellow lambs respectively. Can all the animals become of same color at the end? 

问题的解决基于这样的一个简单的观察。

The solution of this problem is based on the simple observation as follow. 

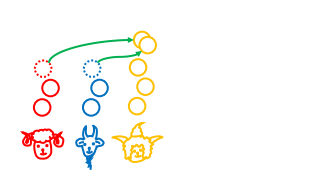每一次物种的转变，两物种的数量只差$\bmod 3$都是定值。

Each time of convertion of species, the difference of number of any pair of two species is a constant $\bmod 3$. 

但是现在，两两的差为$1,1,2\bmod 3$, 所以不论怎么基因突变，都不能有两种数量同时为零。

But now, the differences are $1,1,2\bmod 3$ respectively, so no matter how the gene mutations occur,  there can not have numbers of two species vanishing at the same time. 

 

 

选择$\bmod 3$并不是巧合，这背后有一些数学，下面要来揭示这一点。

Our choice of $\bmod 3$ is not a coincidence, and there are some mathematics behind it. We will illustrate it in the following context. 

记$a,b,c$分别是三种羊，以他们为基张成一个自由Abel群$a\mathbb{Z}+b\mathbb{Z}+c\mathbb{Z}$. 

Denote $a,b,c$ by three kinds of animals, consider $a\mathbb{Z}+b\mathbb{Z}+c\mathbb{Z}$, the free abelian group generated by them. 

那么任何羊的数量状态都是这个群中的一个元素。

Then any state of anmial's numbers is an element in this group. 

鉴于物种的变化，我们商掉关系$a+b-2c, a+c-2b, b+c-2a$. 

Taking into the consideration the change of species, we need to module the relation $a+b-2c, a+c-2b, b+c-2a$. 

这样，可以转化的状态就在商群中相等了。

Then, two states in which one can convert into the other one are equal in the quotient group. 

现在，我们需要一些计算。

Now, we need some calculation. 

$$\begin{array}{l}    \quad a\mathbb{Z}+b\mathbb{Z}+c\mathbb{Z}/(a+b-2c, a+c-2b, b+c-2a)     \\ = a\mathbb{Z}+b\mathbb{Z}+(2a-b)\mathbb{Z}/(a+b-2c, a+c-2b, b+c-2a)     \\     = a\mathbb{Z}+b\mathbb{Z}/(a+b-2(2b-a),b+(2b-a)-2a) \\  = a\mathbb{Z}+b\mathbb{Z}/(3a-3b) \\  = a\mathbb{Z}+(b-a)\mathbb{Z}/(3b-3a) \\ = a\mathbb{Z}+(b-a)\mathbb{Z}/3\mathbb{Z}\\ = \mathbb{Z}\oplus \mathbb{Z}/3\mathbb{Z}    \end{array}$$

在此映射下，$a\mapsto (1,0), b\mapsto (1,1), c\mapsto (1,-1)$. 

Under this isomorphism, $a\mapsto (1,0), b\mapsto (1,1), c\mapsto (1,-1)$. 

所以$15a+19b+20c\mapsto (54, -1)$, 不能等于任何$na,nb,nc$的像。

Therefore  $15a+19b+20c\mapsto (54, -1)$ which cannot equals to any image of $na,nb,nc$. 

同时，我们也发现，在这个问题中，有两个不变量，一个是羊的总数，一个是某两种羊数量之差$\bmod 3$. 

On top of that, we find that, in this problem, there are two invariants, the one is the total number of animals, and the other one is the difference $\bmod 3$ between certain two species. 

 

 

下面我们来看一个类似的问题。

Now, we turn to anthor similar problem. 

很久以前，有三种羊，红羊，蓝羊，黄羊。

Long time ago, there were three kinds of animal, say red sheep, blue goat and yellow lamb. 

他们住在一个名为『魔术农庄』的农场。

They lived in a farm called Magic Farm.

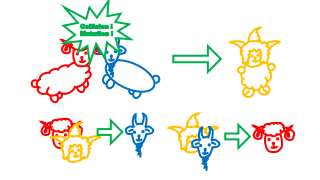如果两只不同的羊相撞，那么他们合体成另一个物种。

If two distinct animals collide, then they will blend into one animal of the other one species. 

有红蓝黄三色羊各15，19，20只，最终会全变成哪种颜色的羊？

There are 15 red sheep, 19 blue goats and 20 yellow lambs respectively. What kind of species will unify the farm at the end? 

这个问题显得怪怪的，似乎没有明显的线索显示最终的颜色是确定的。

This problem is weird, because it is not clear that the final color is determined in advance. 

如果我们只想知道最后能够是什么样子的，只需有下面的观察。

If we just want to know about one of the possible final stages, the following observation is sufficiant. 

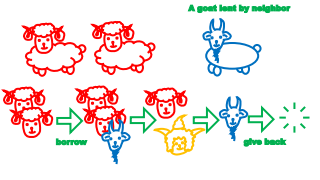如果我们有两只红羊，可以从邻居家借来一只蓝羊，最后可以变成一只蓝羊（然后我们再还回去）。

If we have two red sheep, we can borrow a blue goat from neighbor, then they can finally becomes one blue goat (and we can give it back to our neighbor).   

使用这个技巧，我们可以用不同颜色的羊作为引子，两个两个地除去相同颜色的羊。

Using this trick, we can cancell pair by pair of same species ultizing another species as trigger. 

最终，15，19，20只变成1，1，0只，于是最终变成的是黄羊。

Finally, 15, 19, 20 becomes 1, 1, 0. So the final species is the yellow lamb. 

 

 

如果我们沿着上面问题的思路，我们需要作如下计算。

If we follow the clue of the problem above, we need the following computation. 

$$\begin{array}{l}    \quad a\mathbb{Z}+b\mathbb{Z}+c\mathbb{Z}/(a+b-c,a+c-b,b+c-a) \\     = a\mathbb{Z}+b\mathbb{Z}+(a+b)\mathbb{Z}/(a+(a+b)-b, b+(a+b)-a) \\     = a\mathbb{Z}/2\mathbb{Z} + b\mathbb{Z}/2\mathbb{Z} \\      \cong \mathbb{Z}/2\mathbb{Z} \oplus \mathbb{Z}/2\mathbb{Z}\end{array}$$

其中$a\mapsto (1,0), b\mapsto (0,1), c\mapsto (1,1)$，所以$15a+19b+20c\mapsto (1,1)$. 

Where $a\mapsto (1,0), b\mapsto (0,1), c\mapsto (1,1)$. As a result, $15a+19b+20c\mapsto (1,1)$. 

注意到$na\mapsto (n,0), nb\mapsto (0,n), nc\mapsto (n,n)$，所以$15a+19b+20c\equiv nc$，且$n$是奇数。

Note that $na\mapsto (n,0), nb\mapsto (0,n), nc\mapsto (n,n)$, hence $15a+19b+20c\equiv nc$, with $n$ odd. 

有时无法判断最终的颜色，即$(0,0)$的情况。

Sometimes, the final speices is not determined, that is the case $(0,0)$. 

现在，最后剩下的可能是任何颜色。

Now, the remain kind of animals can be any speices.  

 

不变量令人惊奇地是Klein四元群。

The invariant is amazingly the Klein's group of order 4. 

阶数为2的体现已在上面『借羊』的例子中体现。

The fact that the order is 2 is demonstrated in the example of `borrowing a goat'. 

 

原始问题是

The original problem is

有红黄蓝三色绵羊各15 19 20只，两只异色绵羊可以同时变为第三色，问最后会不会出现 所有绵羊同色的情况？

There are 15, 19 and 20 sheep of color red, yellow and blue respectively. Any pair of sheep of different colors can convert into the rest one color simultaneously. Can all the sheep become of same color at the end? 

为了趣味起见，我编了一个故事。

To make it of more fun, I made a story. 

『类似的问题』是我自己题的。

The `similar problem' is raised by myself.  

这个问题的提法启发自给『孔明棋』。可以利用条带状染Klein四元群来确定最终落子位置。

The raising of this problem is inspired by the game `Peg Solitaire' , where we can know the final position by coloring with Klein group in striped pattern. 

    a b c    
    b c a    
a b c a b c a
b c a b c a b
c a b c a b c
    c a b    
    a b c    

图片是用powerpoint制作的。

The picture is made by powerpoint. 

感谢汤一鸣提供最初的做法，感谢刘奔和我讨论。

Thank for Tang Yiming for his original solution, and for Liu Ben for discussion. 

感谢妈妈的水彩笔。

Thank for my mom's markers. 

posted @ 2019-08-12 02:06  XiongRui  阅读(814)  评论(1)  编辑  收藏  举报