Characterization of Dynkin diagrams
Nowadays, I am reading D.J.Benson's nice book, volume I of Representations and cohomology. I found it has a nice description on Dynkin diagrams. So I want to make a note on it and on it here. If the application is successful, I will have more time on Mathematiques intersting me. If the time permits, I will make anther note about the relationship of root system and Dynkin diagrams.
Contents
- Dynkin diagrams and Euclidean diagrams
- Cartan matrix and characterization of Dynkin diagrams using subadditve functions
- Characterization using positive definity of Cartan's matrix
Dynkin diagrams and Euclidean diagrams
The following labeled graphs are called Dynkin diagrams
- $A_n$($n\geq1$)
![]()
- $B_n$($n\geq 2$)
![]()
- $C_n$($n\geq 2$)
![]()
- $D_n$($n\geq 4$)
![]()
- $E_6$
![]() ; $E_7$
; $E_7$![]() ; $E_8$
; $E_8$![]()
-
$F_4$
![]()
-
$G_2$
![]()
The foot index illustrates the number of nodes. And  ,
, 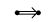 and
and  stands a edge labelled by $(1,1)$, $(2,1)$ and $(3,1)$ respectively.
stands a edge labelled by $(1,1)$, $(2,1)$ and $(3,1)$ respectively.
The following labeled graphs are called Euclidean diagrams
- $\tilde{A}_n$($n\geq 1$)
![]() ; $\tilde{A}_{11}$
; $\tilde{A}_{11}$![]() ; $\tilde{A}_{12}$
; $\tilde{A}_{12}$![]() .
. - $\tilde{B}_n$($n\geq 3$)
![]()
- $\tilde{C}_n$($n\geq 3$)
![]()
- $\tilde{D}_n$($n\geq 5$)
![]()
- $\widetilde{BC}_n$($n\geq 3$)
![]()
- $\widetilde{BD}_n$($n\geq 4$)
![]()
- $\widetilde{CD}_n$($n\geq 4$)
![]()
-
$\tilde{E}_6$
![]() ; $\tilde{E}_7$
; $\tilde{E}_7$![]() ; $\tilde{E}_8$
; $\tilde{E}_8$ ![]()
-
$\tilde{F}_{41}$
![]() ; $\tilde{F}_{42}$
; $\tilde{F}_{42}$![]()
-
$\tilde{G}_{21}$
![]() ; $\tilde{G}_{22}$
; $\tilde{G}_{22}$![]()
The sum of foot index illustrates the number of nodes.
Cartan matrix and characterization of Dynkin diagrams using subadditve functions
Definition. For a labelled graph $G=(V,E)$, defined its Cartan matrix $(c_{xy})_{x,y\in V}$ where $$c_{xy}=2\delta_{xy}-\sum_{\textrm{all edges }x\stackrel{(a,b)}\longrightarrow y} a$$where $\delta_{xy}=1$ if $x=y$ and vanishes if $x\neq y$. A function $n: V\to \mathbb{Z}_{>0}$ is called subadditive if $$\forall y\in V, \qquad \sum_{x\in V} n_xc_{xy}\geq 0$$ And is called additive if $$\forall y\in V, \qquad \sum_{x\in V} n_xc_{xy}= 0$$ Clearly, subadditivity implies additivity.
We will show that Dynkin diagram and Euclidean diagrams are the only finite connected diagrams admitting a subadditive function, and Euclidean diagrams are the only ones admitting an addtive function.
We need three lemmas.
Lemma 1. Any finite connected labelled graph $T$, either $T$ is a Dynkin diagram or there is a Euclidean diagram smaller than $T$. Where "smaller" means both "subgraph" and "smaller" in the numbers of the label. Note that in the definition of labelled graph, all the number in labels are taken to be positive integers.
Proof is just exclude the possibilities of not being Dynkin diagram.
Lemma 2. Suppose $T$ and $T'$ are connected labelled graphs and $T$ is strickly smaller than $T'$, if $n$ is a subadditve function on $T'$, then the restriction of $n$ over $T$ is subadditve but not additive.
Proof. For any vertex $y$ of $T$, we have $$0\leq \sum_x n_xc'_{xy}=2n_y-\sum_{\textrm{all edges } x\stackrel{(a,b)}\longrightarrow y\textrm{ in $T'$}}n_x a\geq 2n_y-\sum_{\textrm{all edges } x\stackrel{(a,b)}\longrightarrow y\textrm{ in $T$}}n_x a=\sum_x n_xc_{xy}$$Since $T$ is strictly smaller, the inequality can not achieve for some $y$. The proof is complete. $\square$
Lemma 3. Any finite connected labelled graph $T$, if $T^{\mathsf{op}}$ admits an additive function, then any subadditve function over $T$ is additive.
Proof. Assume $T^{\mathsf{op}}$ admits an additive function $n$, then $\sum c_{yx}n_x=0$. Then for any subadditive function $m$ over $T$, we have$$0=\sum_ym_y\bigg(\sum_{x} c_{yx}n_x\bigg)=\sum_{x}n_x \bigg(\sum_{y}m_yc_{yx}\bigg)$$The sum is a series of non-negetive integer, so we have $\sum_{y}m_yc_{yx}=0$. $\square$
And it suffices to prove there exists an additive function on each Euclidean diagrams. As following
(To check the additivity, just check that the sum of number "come in" equals to 2 times of the number of point. )
Now, we can conclude the discription of Euclidean diagrams and Dynkin diagrams
Theroem. If a finite connected labelled graph $T$ admits a subaddtive function iff $T$ is either a Dynkin diagram or a Euclidean diagram. If furthermore, $T$ admits an additive function iff$T$ is a Euclidean diagram.
Proof. By the above lemmas.
Characterization using positive definity of Cartan's matrix
Using the characterization above, one can easily deriver the following characerization
Theroem. Given a finite connected labelled graph $T$, let $C$ be its Cartan matrix. $C$ is semidefinite iff $T$ is either a Dynkin diagram or a Euclidean diagram. Furthermore, $C$ is positive definite iff $T$ is a Dynkin diagram.
Proof. For an Euclidean diagram, let $n$ be an additive function, note that the condition of additivity implies for any fixed $x$, $\sum_{y\neq x}\frac{n_y c_{yx}}{n_x}=-2$, then$$\begin{array}{rl}\sum_{x,y\in V}a_xa_yc_{xy} & =2\sum_{x\in V}a_x^2+\sum_{x\neq y} a_xa_yc_{xy} \\ & =-\sum_{x\in V}\frac{a_x^2n_yc_{yx}}{n_x}+\sum_{x\neq y} a_xa_yc_{xy} \\& = -\frac{1}{2}\sum_{x\neq y}\big(\frac{a_x^2n_yc_{yx}}{n_x}+\frac{a_y^2n_xc_{xy}}{n_y}\big)+\sum_{x\neq y} a_xa_yc_{xy} \\ & =-\frac{1}{2}\sum_{x\neq y} n_xn_yc_{xy}\big(\frac{a_x}{n_x}-\frac{a_y}{n_y}\big)^2\geq 0\end{array}$$ Then, it is not difficult to see that the Cartan matrix is positive definite for Dynkin diagram, merely because Dynkin diagrams are exactly the graph strictly smaller than Euclidean diagrams. To prove when $T$ is neither a Dynkin diagram nor a Euclidean diagram. By the lemma above, there are some Euclidean diagram $T'$ strictly smaller than $T$. If $T$ contains all points of $T'$, then $(n_x)$ such that $\sum n_xn_yc_{xy}<0$, otherwise, pick a point, say $v$, in $T$ but not in $T'$, then $n'_x=\begin{cases}n_x & \textrm{$x$ in $T$} \\ \epsilon & x=v \\ 0 & \textrm{otherwise}\end{cases}$, then $$\begin{array}{rl}\sum n'_xn'_y c_{xy} & =\sum n_xn_yc_{xy}+2\epsilon^2+\underbrace{\bigg(\sum_{x\in V}c_{xv}\bigg)}_{<0}\epsilon \\ & \leq 0+ 2\epsilon^2+\underbrace{\bigg(\sum_{x\in V}c_{xv}\bigg)}_{<0}\epsilon\end{array}$$Take $\epsilon$ sufficient small, the above is strictly negetive. $\square$






 ; $E_7$
; $E_7$ ; $E_8$
; $E_8$


 ; $\tilde{A}_{11}$
; $\tilde{A}_{11}$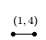 ; $\tilde{A}_{12}$
; $\tilde{A}_{12}$ .
. 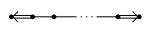
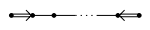




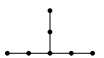 ; $\tilde{E}_7$
; $\tilde{E}_7$ ; $\tilde{E}_8$
; $\tilde{E}_8$ 
 ; $\tilde{F}_{42}$
; $\tilde{F}_{42}$
 ; $\tilde{G}_{22}$
; $\tilde{G}_{22}$

 浙公网安备 33010602011771号
浙公网安备 33010602011771号