【题解】赛艇 [THUPC2018] [P5447]
【题解】赛艇 [THUPC2018] [P5447]
传送门：赛艇 \(\text{[THUPC2018] [P5447]}\)
【题目描述】
给出一个只包含 \(01\) 的大矩阵和一长串运动轨迹，求该轨迹在大矩阵中只覆盖 \(0\) 的合法安放位置个数。
【分析】
一道 \(\text{FFT}\) 做字符串匹配的水题（没想到 \(\text{THU}\) 也会有我这个蒟蒻能做的题目 QAQ）。
还不会这种套路的强烈建议去康康这个，保准一遍看懂。
考虑先将运动轨迹对应的放到大矩阵的左上角（走过的位置设为 \(1\)，其他为 \(0\)），比如样例：
然后把大矩阵和运动轨迹分别折叠成一维数组 \(f,g\)，按照套路卷起来即可，具体实现如下：
设 \(PA(st)=\sum_{i=1}^{n \times m}f(st+i-1)g(i)\)，翻转 \(g\) 得到：\(PA(st)=\sum_{i=1}^{n \times m}f(st+i-1)g(n \times m-i+1)\) \(=\sum_{i+j=st+n \times m}f(i)g(j)\)，当 \(PA(st)=0\) 时可知 \(st\) 为一个合法匹配的起点。
为什么对一维匹配数组跑匹配就是对的呢？
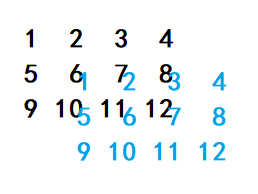
感觉起来不太好理解，画个图瞬间就懂了，如下（黑色为大矩阵，蓝色为轨迹矩阵，矩阵中的数字为对应在一维数组中的编号，假设实际运动轨迹只经过了蓝色数字 \(\{1,2,3,5,6,7\}\)）：
在上图中，匹配起点 \(st\) 为 \((2,2)\)，对应一维编号为 \(6\)，如果根据上面的 \(PA\) 定义式来看，轨迹矩阵中的 \(\{1,2,3,4,5,6,7\}\) 分别与大矩阵中的 \(\{6,7,8,9,10,11,12\}\) 进行了匹配，其中只有蓝色越界数字 \(4\) 对应了黑色越界数字 \(9\)，而剩下的 \(\{1,2,3,5,6,7\}\) 匹配情况都与上图完全吻合。
由于我们判断矩阵是否匹配只用关注未越界合法点，因此可以证明上述做法是正确的。
注意还有一个小问题：必须要保证轨迹矩阵的合法点（即 \(1\)）全部在大矩阵以内。这个可以通过改变 \(st\) 的枚举范围来实现。
时间复杂度为：\(O(nm\log (nm))\) 。
【Code】
#include<algorithm>
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=8388608+3,P=998244353,G=3,inf=2e9;char ch[5000003];
int n,m,T,ans,invG,minx=1,miny=1,maxx,maxy,f[N],g[N],tr[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
inline void NTT(Re *f,Re n,Re op){
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1){
Re len=p>>1,w1=mi(op?invG:G,(P-1)/p);
for(Re st=0;st<n;st+=p)
for(Re j=st,base=1;j<=st+len-1;++j){
Re tmp=(LL)base*f[j+len]%P;
f[j+len]=(f[j]-tmp+P)%P,(f[j]+=tmp)%=P;
base=(LL)base*w1%P;
}
}
}
inline void sakura(Re *f,Re n,Re *g,Re m){//卷卷卷
for(m+=n,n=1;n<=m;n<<=1);Re invn=inv(n);
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P;
NTT(f,n,1);
for(Re i=0;i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
inline int Poi(Re i,Re j){return (i-1)*m+j;}
inline void move(Re &x,Re &y,char op){x+=(op=='s')-(op=='w'),y+=(op=='d')-(op=='a');}
int main(){
// freopen("123.txt","r",stdin);
in(n),in(m),in(T),invG=inv(G);
for(Re i=1;i<=n;++i){
scanf("%s",ch+1);
for(Re j=1;j<=m;++j)f[Poi(i,j)]=(ch[j]=='1');
}
scanf("%s",ch+1);
for(Re i=1,x=1,y=1;i<=T;++i)
move(x,y,ch[i]),minx=min(minx,x),miny=min(miny,y);//获取最小坐标minx,miny得到相对差值cx,cy
Re cx=1-minx,cy=1-miny;g[n*m-Poi(maxx=1+cx,maxy=1+cy)+1]=1;//注意起点别忘了
for(Re i=1,x=1+cx,y=1+cy;i<=T;++i)
move(x,y,ch[i]),maxx=max(maxx,x),maxy=max(maxy,y),g[n*m-Poi(x,y)+1]=1;//获取最大坐标maxx,maxy方便判断越界
sakura(f,n*m,g,n*m);
for(Re i=1;i<=n-maxx+1;++i)
for(Re j=1;j<=m-maxy+1;++j)
ans+=(f[Poi(i,j)+n*m]==0);
printf("%d\n",ans);
}
