【学习笔记】动态规划—斜率优化DP(超详细)
【学习笔记】动态规划—斜率优化DP(超详细)
\(update\ 2020.6.19:\) 临近退役,终于来修锅啦QAQ(更正基础概念上的错误;\(\text{Latex}\) 规范化;重新排版;增加标题号;添加【关于单调性的研究】;添加 \(\text{CDQ}\) 维护斜率优化的例子)
【学习笔记】动态规划—各种 \(\text{DP}\) 优化
【前言】
第一次写这么长的文章。
写完后对斜优的理解又加深了不少(\(update\ 2020.6.19:\) 回过头来看这句话满是讽刺啊,明明这时候连基本的概念都没有理清....)。
本文讲解较详,只要耐心读下去,相信大部分 \(\text{OIer}\) 都能看懂。
斜率优化 \(\text{dp}\),顾名思义就是利用斜率相关性质对 \(\text{dp}\) 进行优化。
斜率优化通常可以由两种方式来理解,需要灵活地运用数学上的数形结合,线性规划思想。
对于这样形式的 \(\text{dp}\) 方程:\(dp[i]=Min/Max(a[i]∗b[j]+c[j]+d[i])\),其中 \(b\) 严格单调递增。
该方程的关键点在于 \(a[i]*b[j]\) 这一项,它既有 \(i\) 又有 \(j\),于是单调队列优化不再适用,可以尝试使用斜率优化。
一.【理解方式】
以 【模板】 玩具装箱 \(\text{toy [P3195]}\) 为例,两种斜优的理解方式。
设 \(S[n]=\sum_{i=1}^n(C[i]+1)\),用 \(dp[i]\) 表示装好前 \(i\) 个的最小花费,则转移方程为:\(dp[i]=min(dp[j]+(S[i]−S[j]-1-L)^2)\)。
为方便描述,将 \(\text{L}\) 提前加 \(1\),再把 \(min\) 去掉,得到状态转移方程:\(dp[i]=dp[j]+(S[i]−S[j]-L)^2\)。
化简得:\(dp[i]=S[i]^2-2S[i]L+dp[j]+(S[j]+L)^2-2S[i]S[j]\)
1.【代数法(数形结合)】
只含 \(\text{L}\) 的项对于每一个 \(i\) 的择优筛选过程都是完全一样的值,只含 \(Function(i)\) 的项在一次 \(i\) 的择优筛选过程中不变,含 \(Function(j)\) 的项可能会不断变化(在本题中表现为为严格单增)。
我们以此为划分依据,把同类型的项用括号括起来,即:\(dp[i]=(-2S[i]S[j])+(dp[j]+(S[j]+L)^2)+(S[i]^2-2S[i]L)\)
(1).【维护一个凸包】
设 \(j_1,j_2\) \((0 \leqslant j_1<j_2<i)\) 为 \(i\) 的两个决策点,且满足决策点 \(j_2\) 优于 \(j_1\),
有:\((-2S[i]S[j_2])+(dp[j_2]+(S[j_2]+L)^2)+(S[i]^2-2S[i]L) \leqslant (-2S[i]S[j_1])+(dp[j_1]+(S[j_1]+L)^2)+(S[i]^2-2S[i]L)\)
即:\((-2S[i]S[j_2])+(dp[j_2]+(S[j_2]+L)^2) \leqslant (-2S[i]S[j_1])+(dp[j_1]+(S[j_1]+L)^2)\)
划重点:此处移项需要遵循的原则是:参变分离。将 \(Function(i)\) 视作未知量,用 \(Function(j)\) 来表示出 \(Function(i)\) 。
移项得:\(-2S[i](S[j_2]-S[j_1]) \leqslant (dp[j_1]+(S[j_1]+L)^2)-(dp[j_2]+(S[j_2]+L)^2)\)
\(\because C[j] \geqslant 1\)
\(\therefore S[j+1] > S[j]\)
\(又 \because j_2 > j_1\)
\(\therefore S[j_2]-S[j_1]>0\)
\(\therefore 2S[i] \geqslant \frac {(dp[j_2]+(S[j_2]+L)^2)-(dp[j_1]+(S[j_1]+L)^2)} {S[j_2]-S[j_1]}\)
设 \(Y(j)=dp[j]+(S[j]+L)^2,X(j)=S[j]\),
即 \(2S[i] \geqslant \frac {Y(j_2)-Y(j_1)} {X(j_2)-X(j_1)}\)
显然等式右边是一个关于点 \(P(j_2)\) 和 \(P(j_1)\) 的斜率式,其中 \(P(j)=(X(j),Y(j))=(S[j],dp[j]+(S[j]+L)^2)\)。
也就是说,如果存在两个决策点 \(j_1,j_2\) 满足 \((0 \leqslant j_1<j_2<i)\),使得不等式 \(\frac {Y(j_2)-Y(j_1)} {X(j_2)-X(j_1)} \leqslant 2S[i]\) 成立,或者说 使得 \(P(j_2),P(j_1)\) 两点所形成直线的斜率小于等于 \(2S[i]\),那么决策点 \(j_2\) 优于 \(j_1\)。
划重点:斜优灵活多变,细节麻烦也多,所以尽量将问题模式化。
比如这里的最终公式,尽量化为 \(\frac {(j)-(j')} {(j)-(j')}\) 的形式,而不是 \(\frac {(j)-(j')} {(j')-(j)}\) ,虽然直接做一般也不会出什么问题,但这样子可以方便理解,方便判断凸包方向等等。
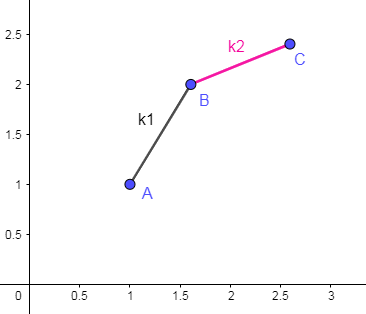
假设有酱紫的三个点 \(P(j_1),P(j_2),P(j_3)\),\(k_1,k_2\) 为斜率,如下图所示情况(三点分别为 \(A,B,C\)):
显然有 \(k_2 < k_1\)。设 \(k_0=2S[i]\),由上述结论可知:
\((a).\) 若 \(k_1 \leqslant k_0\),则 \(j_2\) 优于 \(j_1\) 。反之,若 \(k_1 > k_0\),则 \(j_1\) 优于 \(j_2\) 。
\((b).\) 若 \(k_2 \leqslant k_0\),则 \(j_3\) 优于 \(j_2\) 。反之,若 \(k_2 > k_0\),则 \(j_2\) 优于 \(j_3\) 。
于是这里可以分三种情况来讨论:
\((1).\) \(k_0 < k_2 < k_1\)。由 \((a),(b)\) 可知:\(j_1\) 优于 \(j_2\) 优于 \(j_3\) 。
\((2).\) \(k_2 \leqslant k_0 < k_1\)。由 \((a),(b)\) 可知:\(j_1\) 和 \(j_3\) 均优于 \(j_2\)。
\((3).\) \(k_2 < k_1 \leqslant k_0\)。由 \((a),(b)\) 可知:\(j_3\) 优于 \(j_2\) 优于 \(j_1\) 。
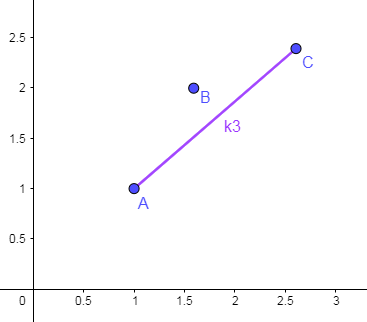
可以发现,对于这三种情况,\(j_2\) 始终不是最优解,于是我们可以将 \(j_2\) 从候选决策点中踢出去(删除),只留下 \(j_1\) 和 \(j_3\),删后的情况如下图所示:
我们要对某一个问题的解决方案进行优化改进,无非就是关注两个要点:正确性和高效性(很多时候高效性都体现为单调性)。
酱紫做的正确性是毋庸置疑的,因为在 \(j_1\) 和 \(j_3\) 其中必定有一个比 \(j_2\) 更优,所以删除 \(j_2\) 对答案没有任何影响。
那么高效性呢?自己在脑子里面 \(yy\) 一下,在一个坐标系的第一象限中(本题中 \(X(j)\) 和 \(Y(j)\)均大于等于 \(0\),至于为什么这里要说等于,下面会提到),有若干个离散的点,任取三点,如果左边斜率大于右边斜率,则形成了上述情况,必定会删点,因而消除这种情况。所以将最后留下来的点首位相连,其形成的各个线段斜率从左到右必定是单调递增的(有可能非严格递增,这个问题之后再讨论)。
如果学习过计算几何相关知识,会意识到这个过程其实与求凸包算法是类似的。(顺手丢一个广告:【学习笔记】计算几何全家桶)
实际上在图中选取最靠左下面、下面、右下面的点首位相连,就是最后留下来的点了,它们形成了一个下凸包,即凸包(又名凸壳)的下半部分(不严谨的讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边形,它能包含点集中所有的点——摘自百度百科)。
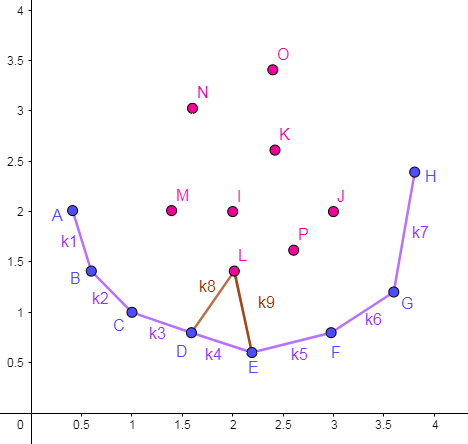
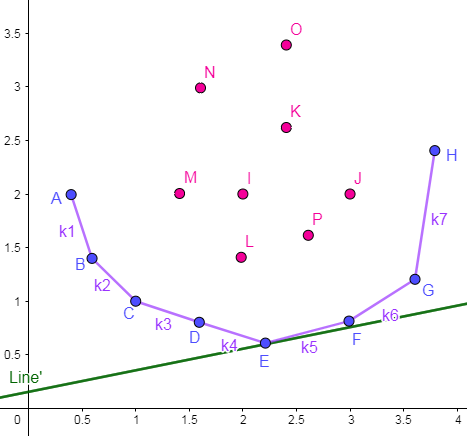
维护出的图形如下图所示:
可以尝试在凸包围起来的区域内任意取一点,其必定能在包围圈上找到两个点使得该点可被删除。如上 \(\text{L}\) 点,它与 \(D,E\) 两点形成了一个可删点图形。
注意:图中 \(C,D,E\) 故意画成了三点一线,而实际上点 \(D\) 是可以删去的,且严格凸包不允许存在这种情况。关于去重的细节问题后面会提到。
同理,如果把不等式 \(\frac {Y(j_2)-Y(j_1)} {X(j_2)-X(j_1)} \leqslant k_0[i]\) 改为 \(\frac {Y(j_2)-Y(j_1)} {X(j_2)-X(j_1)} \geqslant k_0[i]\),那么维护出来的就是一个上凸包。
(2).【寻找最优决策点】
在一次决策点的寻找中,易知下凸包点集里总会存在一点,使得它与左邻点形成的斜率小于等于 \(k_0\) ,与右邻点形成的斜率大于 \(k_0\) 。
例如上图中的 \(E\) 点,设 \(k_4 \leqslant k_0 < k_5\) 由于凸包上面的斜率呈单增态,那么有:\(k_1 < k_2 < k_3 < k_4 \leqslant k_0 < k_5 < k_6 < k_7\),所以决策点 \(E\) 优于其他所有点,即 \(E\) 就是 \(dp[i]\) 的最优决策点。
如果暴力查找的话,就是从第一个点开始向后扫描,找到第一个斜率大于 \(k_0\) 的线段,其左端点即为最优决策点。由于凸包上的斜率依次递增,可以二分快速得到这个点。
2.【线性规划】
先回顾一下模板题的 \(\text{dp}\) 方程:\(dp[i]=S[i]^2-2S[i]L+dp[j]+(S[j]+L)^2-2S[i]S[j]\)。
对其进行移项变化,变成形如 \(y=kx+b\) 的点斜式。
划重点:移项要遵循的原则是:把含有 \(function(i)*function(j)\) 的表达式看作斜率 \(k_0\) 乘以未知数 \(x\),含有 \(dp[i]\) 的项必须要在 \(b\) 的表达式中,含有 \(function(j)\) 的项必须在 \(y\) 的表达式中。如果未知数 \(x\) 的表达式单调递减,最好让等式两边同乘个 \(-1\),使其变为单增。
至于为什么说要让 \(x\) 的表达式单增,emm...其实是为了让一些较简单的问题模式化,不易出错,如果你非要单减,可以尝试倒序枚举,至于是否正确,具体实现需要注意的玄学问题等等,因为觉得太麻烦没有细想,我也不清楚会遇到什么问题。
例如此题,原 \(\text{dp}\) 方程可化为:
\((2S[i])S[j]+(dp[i]-S[i]^2+2S[i]L)=(dp[j]+(S[j]+L)^2)\)
其中 \(k_i=2S[i],\) \(x_i=S[j],\) \(b_i=dp[i]-S[i]^2+2S[i]L,\) \(y_i=dp[j]+(S[j]+L)^2\)。
其实也可以化为:
\((2S[i])(S[j]+L)+(dp[i]-S[i]^2)=(dp[j]+(S[j]+L)^2)\)
其中 \(k_i=2S[i],\) \(x_i=S[j]+L,\) \(b_i=dp[i]-S[i]^2,\) \(y_i=dp[j]+(S[j]+L)^2\)。
还可以化为 \(...\)
\(...\)
只要满足上述移项原则,对答案是没有任何影响的。
这里以第一种形式为例,先画出草图:
(1).【高中数学知识】
我们的目的是求出一个最优决策点 \(j\) 使得 \(dp[i]\) 最小,又因为 \(b[i]=dp[i]-S[i]^2\) ,所以就是要找到某个点使这条直线经过它时算出来的 \(b\) 最小,即是高中数学课本上的线性规划问题。
(2).【寻找最优决策点】
如图所示,点 \(E\) 即为最优决策点。显然,这个使得 \(b\) 最小的最优决策点位于下凸包点集中,且与上述代数法求得的点一致。
3.【两种思考方式的结合】
强烈推荐用线性规划思想主导思考过程,因为图形的变幻较直观,更重要的是:在某某变量不满足单调性时,通过图形可以迅速做出判断并改变策略(在后面【关于单调性的研究】中会详细解释)。
而代数法通常在不便于识别方程特征时起一个转换思维方向的作用,因为有些题可能会直接出现 \(\frac{Y(j)-Y(j')}{X(j)-X(j')}\) 的形式,需要通过一系列代数推导后再绘草图模拟决策。
二.【维护凸包】
实际上只要让维护的凸包方向相同,两种思考方式的代码是一模一样的。
用单调队列维护凸包点集,操作分三步走:
\((1).\) 进行择优筛选时,在凸包上找到最优决策点 \(j\) 。
\((2).\) 用最优决策点 \(j\) 更新 \(dp[i]\) 。
\((3).\) 将 \(i\) 作为一个决策点加入图形并更新凸包(如果点 \(i\) 也是 \(dp[i]\) 的决策点之一,则需要将 \((3)\) 换到最前面)。
在本题中步骤 \((3)\) 的具体操作为:判断当队尾的点与点 \(i\) 形成可删点图形时,出队直至无法再删点,然后将 \(i\) 加入队列。
在判断可删图形时有两种方法(以 下凸包 为例),一种是 slope(Q[t-1],Q[t])<=slope(Q[t],i),另一种是 slope(Q[t-1],Q[t])<=slope(Q[t-1],i),都表示出现了可以删去点 \(Q[t]\) 的情况(只要对边界、去重的处理足够严谨,两种写法是没有区别的)。其中 \(Q\) 是维护凸包点集的队列。
该做法时间复杂度为 \(O(n\log n)\),瓶颈在于二分寻找最优决策点。
三.【再优化】
运用决策单调性进行优化。决策单调性相关基础知识见 【学习笔记】动态规划—各种 \(\text{DP}\) 优化,这里只放一下定义:
设 \(j_0[i]\) 表示 \(dp[i]\) 转移的最优决策点,那么决策单调性可描述为 \(\forall i\leqslant i',j_0[i]\leqslant j_0[i']\)。也就是说随着 \(i\) 的增大,所找到的最优决策点是递增态(非严格递增)。
(1).【决策单调性证明】
还是以 玩具装箱 为例,来简单证一波决策单调性,方法采用四边形不等式。
显然,本题的转移方程呈现出了 \(dp[i]=min(dp[j]+w(i,j))\) 的形式,即 \(1D/1D\) 动态规划方程,其中 \(w(i,j)=(S[i]−S[j]-1-L)^2\)。
\(证明:设\) \(Q=S[i]−S[j]-1-L\)
\(\therefore w(i,j)=(S[i]−S[j]-1-L)^2=Q^2\)
\(\begin{aligned} \therefore w(i+1,j+1)=&(S[i+1]−S[j+1]-1-L)^2\\ =&((S[i]+C[i+1]+1)−(S[j]+C[j+1]+1)-1-L)^2\\ =&(Q+C[i+1]-C[j+1])^2 \end{aligned}\)
\(\begin{aligned} w(i,j+1)=&(S[i]−S[j+1]-1-L)^2\\ =&(S[i]−(S[j]+C[j+1]+1)-1-L)^2\\ =&(Q-C[j+1]-1)^2 \end{aligned}\)
\(\begin{aligned} w(i+1,j)=&(S[i+1]−S[j]-1-L)^2\\ =&((S[i]+C[i+1]+1)−S[j]-1-L)^2\\ =&(Q+C[i+1]+1)^2 \end{aligned}\)
\(\therefore w(i,j)+w(i+1,j+1)=2Q^2+2C[i+1]Q-2C[j+1]Q+C[i+1]^2-2C[i+1]C[j+1]+C[j+1]^2\)
\(\therefore w(i+1,j)+w(i,j+1)=2Q^2+2C[i+1]Q-2C[j+1]Q+C[i+1]^2+2C[i+1]+2C[j+1]+C[j+1]^2+2\)
\(\therefore w(i,j)+w(i+1,j+1)-w(i+1,j)+w(i,j+1)=-2(C[i+1]+1)(C[j+1]+1)\)
\(又 \because C[i],C[j] \geqslant 1\)
\(\therefore -2(C[i+1]+1)(C[j+1]+1) \leqslant -8\)
\(\therefore w(i,j)+w(i+1,j+1) \leqslant w(i+1,j)+w(i,j+1)\)
四边形不等式成立,所以此方程具有决策单调性。
证毕。
(2).【单调队列】
由于最优决策点递增,可以用单调队列对其进行维护。操作 \((2),(3)\) 不需要改动,操作 \((1)\) 改为:判断当队首的第一根线段斜率小于等于 \(k_0[i]\) 时就出队,直至斜率大于 \(k_0[i]\),此时的队首即为最优决策点。
正确性显然。因为随着 \(i\) 的变大,最优决策点 \(j_0[i]\) 也会跟着变大,如果已知某个点在当前情况下不够侑秀,那么在这之后也一定不会作为最优决策点,所以可以直接出队。
时间复杂度为 \(O(n)\) 。
(3).【再证决策单调性】
一样的,两种思路。
先观察 \(k_0[i]\) 的表达式:\(k_0[i]=2S[i]\) ,明显在本题中 \(k_0\) 呈单增态。
【代数法】
\(k_0[i]\) 递增就说明我们找到的第一个斜率大于 \(k_0[i]\) 的线段在不断地向后移,也就是说,如果我们找到了某一个最优决策点 \(j\),那么在下一次决策中,最优决策点 \(j'\) 必定在 \(j\) 的后面。
决策单调性得证。
【线性规划】
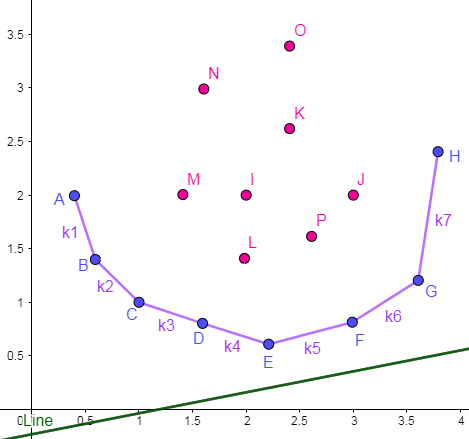
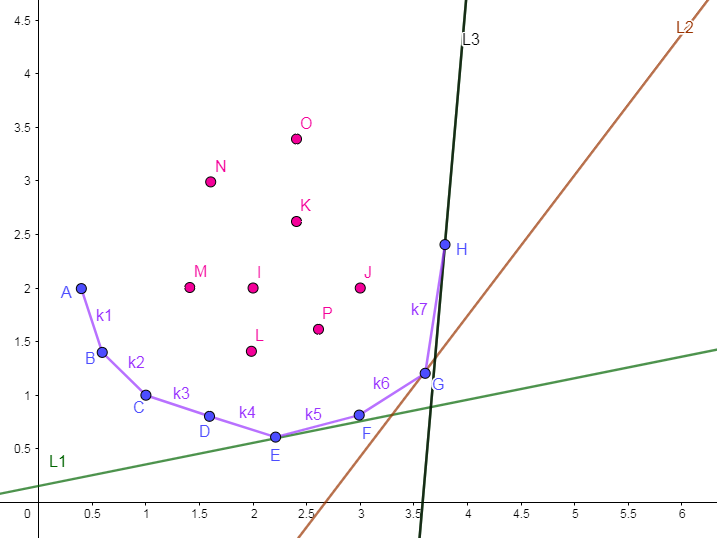
画出草图:
直线 \(Line_i\) 的斜率 \(k_0[i]\) 递增,
由图可知最优决策点在递增。
决策单调性得证。
【其他】
从这个角度来看的话,貌似决策单调性和 \(X(j),k_0[i]\) 的单调性是相通的?
于是一个结论就出现了:如果 \(X(j),k_0[i]\) 均单调不减,则该方程必定有决策单调性(自己瞎 \(yy\) 的,不敢肯定一定正确)。
四.【Code】
这道题 \(...\) 数据太水了 \(...\) 我一开始 \(\text{L}\) 忘了加 \(1\) 居然还过了 \(...\)
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register LL
const int N=5e4+5;
LL i,j,n,L,h=1,t=0,Q[N],S[N],dp[N];
//S[n]=∑C[i]+1, dp[i]=min(dp[j]+(S[i]-(S[j]+L+1))^2),++L
//dp[i]=S[i]^2-2*S[i]*L+dp[j]+(S[j]+L)^2-2S[i]*S[j]
//(2*S[i]) * S[j] + (dp[i]-S[i]^2+2S[i]L)=(dp[j]+(S[j]+L)^2)
// k * x + b = y
inline LL min(Re a,Re b){return a<b?a:b;}
inline LL X(Re j){return S[j];}
inline LL Y(Re j){return dp[j]+(S[j]+L)*(S[j]+L);}
inline long double slope(Re i,Re j){return (long double)(Y(j)-Y(i))/(X(j)-X(i));}//记得开long double
int main(){
scanf("%lld%lld",&n,&L);++L;
for(i=1;i<=n;S[i]+=S[i-1]+1,++i)scanf("%lld",&S[i]);
Q[++t]=0;//重中之重
for(i=1;i<=n;++i){
while(h<t&&slope(Q[h],Q[h+1])<=2*S[i])++h;//至少要有两个元素 h<t。出队判断时尽量加上等号
dp[i]=dp[j=Q[h]]+(S[i]-S[j]-L)*(S[i]-S[j]-L);
while(h<t&&slope(Q[t-1],Q[t])>=slope(Q[t-1],i))--t;//至少要有两个元素 h<t。入队判断时尽量加上等号
Q[++t]=i;
}
printf("%lld",dp[n]);
}
五.【各种玄学问题】
(ノ°ο°)ノ前方高能预警 (*°ω°*)ノ"非战斗人员请撤离!! *・_・)ノ
\((1).\) 写出 \(\text{dp}\) 方程后,要先判断能不能使用斜优,即是否存在 \(function(i)*function(j)\) 的项或者 \(\frac{Y(j)-Y(j')}{X(j)-X(j')}\) 的形式。
\((2).\) 通过大小于符号或者 \(b\) 中 \(dp[i]\) 的符号结合题目要求 \((min/max)\) 判断是上凸包还是下凸包,不要见一个方程就直接盲猜一个下凸。
\((3).\) 当 \(X(j)\) 非严格递增时,在求斜率时可能会出现 \(X(j_1)=X(j_2)\) 的情况,此时最好是写成这样的形式:return Y(j)>=Y(i)?inf:-inf,而不要直接返回 \(inf\) 或者 \(-inf\),在某些题中情况较复杂,如果不小心画错了图,返回了一个错误的极值就完了,而且这种错误只用简单数据还很难查出来。
\((4).\) 注意比较 \(k_0[i]\) 和 \(slope(j_1,j_2)\) 要写规范,要用右边的点减去左边的点进行计算(结合 \((3)\) 来看,可防止返回错误的极值),如果用的代数法理解,写出了 (X(j2)-X(j1))*k0<=Y(j2)-Y(j1) 或 (X(j2)-X(j1))*k0<=Y(j2)-Y(j1),而恰巧 \(j_1,j_2\) 又写反了,便会出现等式两边同除了负数却没变号的情况。当然用 \(k_0\) 和 \(\frac {Y(j_2)-Y(j_1)}{X(j_2)-X(j_1)}\) 进行比较是没有这种问题的。
\((5).\) 队列初始化大多都要塞入一个点 \(P(0)\),比如 玩具装箱 \(\text{toy}\),需要塞入 \(P(S[0],dp[0]+(S[0]+L)^2)\) 即 \(P(0,0)\),其代表的决策点为 \(j=0\)。
\((6).\) 手写队列的初始化是 h=1,t=0,由于塞了初始点导致 \(t\) 加 \(1\),所以在一些题解中可以看到 h=t=1 甚至是 h=t=0,h=t=2 之类的写法,其实是因为省去了塞初始点的代码。它们都是等价的。
\((7).\) 手写队列判断不为空的条件是 h<=t,而出入队判断都需要有至少 \(2\) 两个元素才能进行操作。所以应是 h<t 。
\((8).\) 计算斜率可能会因为向下取整而出现误差,所以 \(slope\) 函数最好设为 \(long\) \(double\) 类型。
\((9).\) 有可能会有一部分的 \(\text{dp}\) 初始值无法转移过来,需要手动提前弄一下,例如 摆渡车 \(\text{[P5017]}\)。
\((10).\) 在比较两个斜率时,尽量写上等于,即 <= 和 >= 而不是 < 和 >。这样写对于去重有奇效(有重点时会导致斜率分母出锅),但不要以为这样就可以完全去重,因为要考虑的情况可能会非常复杂,所以还是推荐加上 \((3)\) 中提到的特判,确保万无一失。
六.【关于单调性的研究】
划重点:注意是否具有单调性,不要盲目地使用单调队列进行维护。
(1).【X(j) 单增与单减】
将方程变为 \(\frac {Y(j_2)-Y(j_1)} {X(j_2)-X(j_1)} \leqslant k_0[i]\) 或者 \(\frac {Y(j_2)-Y(j_1)} {X(j_2)-X(j_1)} \geqslant k_0[i]\) 或者 \(kx+b=y\) 的形式,变化要遵循之前提到的原则,尤其是 \(X(j)\) 的单调性,结合图形会更好理解(目的是将单减的形式变为单增,方便维护)。
(2).【决策点横坐标 X(j) 不单调】
注意:\(X(j)\) 的单调性会影响凸包维护方式的选择。
如果决策点横坐标 \(X(j)\) 不存在单调性该怎么办(既不单增也不单减)?
(假设此时 \(k_0[i]\) 仍然单调)
此时维护凸包就不能用单调队列了,因为插入点时可能会插到凸包点集中间的某个位置,而队列是不支持这种操作的,需要用到平衡树维护或者用 \(\text{CDQ}\) 分治提供单调性(后面会讲到)。
这里有计算几何基础的话会更易理解,因为上面维护图形时的删点操作与水平序 \(\text{Graham}\) 扫描法求凸包是类似的,而扫描法的前提为:点集呈水平序,即点从左至右依次排列(体现为 \(X(j)\) 单调不减)。
(3).【待决策点斜率 K0[i] 不单调】
注意:\(k_0[i]\) 的单调性会影响寻找最优决策点方式的选择。
如果斜率 \(k_0[i]\) 不存在单调性该怎么办?
(假设此时 \(X(j)\) 仍然单调)
我们仍可以用队列维护凸包点集,但不知道每一次会在什么地方取得最优决策点,所以必须要保留整个凸包以确保决策有完整的选择空间,也就是说不能弹走队首,同时查找答案也不能直接取队首,只能使用二分。
- 【模板】 任务安排 \(3\)(可以证明该题不具有决策单调性)
(4).【X(j) 与 K0[i] 均不单调】
现在来看 \(k_0[i]\) 与 \(X(j)\) 均不单调的情况:
此时无法再用队列维护凸包了,但平衡树本就支持查询前驱、后继,直接把 \(k_0[i]\) 丢进去询问即可。
而 \(\text{CDQ}\) 就更有意思了:在 \((2)\) 中做法的基础上恰好还能再加一维偏序!
我们直接人为地排出单调性,像普通单调队列那样维护就可以了(代码放后面)。
七.【例题】
1.【预处理DP 初始值】
去年 \(noip\) 普及组的题(雾)。
【Code】
#include<cstdio>
#define Re register int
const int N=4e6+105;
int i,j,n,m,h=1,t=0,T,ti,ans=2e9,G[N],S[N],Q[N],dp[N];
inline int min(Re a,Re b){return a<b?a:b;}
// i
//dp[i]=min(dp[j]+ ∑(i-T[k]))
// k=j+1
//dp[i]=dp[j]+(G[i]-G[j])*i-(S[i]-S[j])
//(i) * G[j] + (dp[i]+S[j]-i*G[i]) = (dp[j]+S[j])
// k * x + b = y
inline int X(Re j){return G[j];}
inline int Y(Re j){return dp[j]+S[j];}
inline long double slope(Re i,Re j){return X(i)==X(j)?(Y(j)>Y(i)?2e9:-2e9):(long double)(Y(j)-Y(i))/(long double)(X(j)-X(i));}
int main(){
scanf("%d%d",&n,&m);
for(i=1;i<=n;T=-min(-T,-ti),++G[ti],S[ti]+=ti,++i)scanf("%d",&ti);
for(i=1;i<T+m;++i)G[i]+=G[i-1],S[i]+=S[i-1];
for(i=0;i<m;++i)dp[i]=G[i]*i-S[i];//提前处理dp初始值
Q[++t]=0;
for(i=m;i<T+m;++i){
while(h<t&&slope(Q[h],Q[h+1])<=i)++h;
dp[i]=dp[j=Q[h]]+(G[i]-G[j])*i-S[i]+S[j];
while(h<t&&slope(Q[t-1],Q[t])>=slope(Q[t-1],i-m+1))--t;
Q[++t]=i-m+1;//(j+1)+m<=i
}
for(i=T;i<T+m;++i)ans=min(ans,dp[i]);
printf("%d",ans);
}
2.【单调队列+二分】
【题目描述】
有 \(N\) 个任务等待完成(顺序不得改变),这 \(N\) 个任务被分成若干批,每批包含相邻的若干任务。从时刻 \(0\) 开始,这些任务被分批加工,第 \(i\) 个任务单独完成所需的时间是 \(T_i\) 。只有一台机器,在每批任务开始前,机器需要启动时间 \(S\),完成这批任务所需的时间是各个任务需要时间的总和(同一批任务将在同一时刻完成)。每个任务的费用是它的完成时刻乘以它的费用系数 \(F_i\)。请确定一个分组方案,使得总费用最小。
【数据范围】
\(T1:\) \(1 \leqslant N \leqslant 5000, 0 \leqslant S \leqslant 50,1 \leqslant T_i, F_i \leqslant 100\)
\(T2:\) \(1 \leqslant N \leqslant 10000, 0 \leqslant S \leqslant 50,1 \leqslant T_i, F_i \leqslant 100\)
\(T3:\) \(1 \leqslant N \leqslant 300000, 1 \leqslant S\leqslant 512,0 \leqslant F_i \leqslant 512,|T_i| \leqslant 512\)
(1).【T1】
设 \(ST[i]=\sum_{j=1}^i T[j],SF[i]=\sum_{j=1}^i F[j]\)
\(\text{dp}\) 方程很简单:\(dp[p][i]=min(dp[p-1][j]+(ST[i]+p\times S)(SF[i]-SF[j]))\),但是 \(O(n^3)\) 的时间复杂度连 \(T1\) 都过不了。
由于不知道每一次分段之前已经分了多少,所以需要用一维空间和一层循环来表示这个信息,从而知道 \(S\) 需要乘以多少。
那么可以反过来,用一种名为费用提前计算的经典思想来进行优化(据说这个叫未来 \(\text{dp}\)),每分出一批任务,那么对于这之后的每一个任务都需要多出一个 \(S\) 的时间,所以可以直接计算 \(S\) 对后面的影响。
即:\(dp[i]=min(dp[j]+ST[i](SF[i]-SF[j])+S(SF[n]-SF[j]))\)
压成了 \(O(n^2)\) 后,\(T1\) 就可以 \(\text{AC}\) 了,但它还能继续优化。
(2).【T2】
先转化为斜率式看看?
\((S+ST[i]) * SF[j] + (dp[i]-ST[i]*SF[i]-S\times SF[i]) = (dp[j])\)
其中 \(k=S+ST[i],\) \(x=SF[j],\) \(b=dp[i]-ST[i]\times SF[i]-S\times SF[i],\) \(y=dp[j]\) 。
决策点要使得 \(dp[i]\) 尽量小,且 \(S+ST[i]\) 和 \(SF[j]\) 都严格单增,所以直接用单调队列维护一个下凸包即可。
时间复杂度为 \(O(n)\) 。
【Code】
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register LL
const int N=1e4+5;
LL i,j,n,h=1,t=0,S,Q[N],ST[N],SF[N],dp[N];
//dp[p][i]=min(dp[p-1][j]+(ST[i]+S*p)*(SF[i]-SF[j]));
//dp[i]=dp[j]+ST[i]*(SF[i]-SF[j])+S*(SF[n]-SF[j]);
//(S+ST[i]) * SF[j] + (dp[i]-ST[i]*SF[i]-S*SF[i]) = (dp[j])
// k * x + b = y
inline LL min(Re a,Re b){return a<b?a:b;}
inline LL X(Re j){return SF[j];}
inline LL Y(Re j){return dp[j];}
inline long double slope(Re i,Re j){return (long double)(Y(j)-Y(i))/(X(j)-X(i));}
int main(){
scanf("%lld%lld",&n,&S);
for(i=1;i<=n;ST[i]+=ST[i-1],SF[i]+=SF[i-1],++i)scanf("%lld%lld",&ST[i],&SF[i]);
Q[++t]=0;
for(i=1;i<=n;++i){
while(h<t&&slope(Q[h],Q[h+1])<(S+ST[i]))++h;
dp[i]=dp[j=Q[h]]+ST[i]*(SF[i]-SF[j])+S*(SF[n]-SF[j]);
while(h<t&&slope(Q[t-1],Q[t])>slope(Q[t-1],i))--t;
Q[++t]=i;
}
printf("%lld",dp[n]);
}
(3).【T3】
因 \(F_i\) 可等于 \(0\),\(X(j)\) \((\) 即 \(SF[i])\) 非严格递增,所以需要特判 \(X(j_1)=X(j_2)\) 的情况(但仍具有单调性,可以使用队列维护凸包)。
因 \(T_i\) 可小于 \(0\),\(k_0[i](\) 即 \(S+ST[i])\) 无单调性,所以不具有决策单调性,可以用四边形不等式进行证明:
该 \(\text{dp}\) 方程显然为 \(dp[i]=dp[j]+w(i,j)\) 的形式,其中 \(w(i,j)=ST[i](SF[i]-SF[j])+S(SF[n]-SF[j])\) 。
\(\text{证明:}\) \(\text{设}\) \(Q=S(SF[n]-SF[j])\)
\(\therefore w(i,j)=ST[i](SF[i]-SF[j])+Q\)
\(\begin{aligned} \therefore w(i+1,j+1)=&ST[i+1]SF[i+1]-ST[i+1]SF[j+1]+S(SF[n]-SF[j+1])\\ =&ST[i+1]SF[i+1]-SF[j+1]*(ST[i]+T[i+1])+Q-S\times F[j+1]\\ \end{aligned}\)
\(\begin{aligned} w(i,j+1)=&ST[i](SF[i]-SF[j+1])+Q-S\times F[j+1]\\ =&ST[i]SF[i]-ST[i]SF[j+1]+Q-S\times F[j+1]\\ \end{aligned}\)
\(\begin{aligned} w(i+1,j)=&ST[i+1](SF[i+1]-SF[j])+Q\\ =&ST[i+1]SF[i+1]-ST[i+1]SF[j]+Q\\ =&ST[i+1]SF[i+1]-ST[i]SF[j]-T[i+1]SF[j]+Q \end{aligned}\)
\(\therefore w(i,j)+w(i+1,j+1)=ST[i](SF[i]-SF[j])+ST[i+1]SF[i+1]-SF[j+1](ST[i]+T[i+1])+2Q-S\times F[j+1]\)
\(\therefore w(i+1,j)+w(i,j+1)=ST[i]SF[i]-ST[i]SF[j+1]+ST[i+1]SF[i+1]-ST[i]SF[j]-T[i+1]SF[j]+2Q-S\times F[j+1]\)
\(\therefore w(i,j)+w(i+1,j+1)-w(i+1,j)+w(i,j+1)=-F[j+1]*T[i+1]\)
\(\text{又} \because 0 \leqslant F_i \leqslant 512,-512 \leqslant T_i \leqslant 512\)
\(\therefore \text{当} T_i \leqslant 0 时,w(i,j)+w(i+1,j+1) \geqslant w(i+1,j)+w(i,j+1)\)
\(\text{当} T_i \geqslant 0 \text{时},w(i,j)+w(i+1,j+1) \leqslant w(i+1,j)+w(i,j+1)\)
四边形不等式不一定成立,所以此题不具有决策单调性。
证毕。
此时需要在队列中二分查找最优决策点。
时间复杂度为 \(O(n\log n)\) 。
【Code】
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register LL
const int N=3e5+5;
LL i,j,n,h=1,t=0,S,Q[N],ST[N],SF[N],dp[N];
//dp[p][i]=min(dp[p-1][j]+(ST[i]+S*p)*(SF[i]-SF[j]));
//dp[i]=dp[j]+ST[i]*(SF[i]-SF[j])+S*(SF[n]-SF[j]);
//(S+ST[i]) * SF[j] + (dp[i]-ST[i]*SF[i]-S*SF[i]) = (dp[j])
// k * x + b = y
//ti可小于0,所以ST[i]非递增,只可二分
//fi可等于0,所以SF[i](X)非严格递增,因此需要特判X(i)==X(j)的情况
inline LL min(Re a,Re b){return a<b?a:b;}
inline LL X(Re j){return SF[j];}
inline LL Y(Re j){return dp[j];}
inline long double slope(Re i,Re j){return X(j)==X(i)?(Y(j)>=Y(i)?1e18:-1e18):(long double)(Y(j)-Y(i))/(X(j)-X(i));
}//由于需要二分查找,多了一些限制:队列里不能有在同一位置的点,返回inf还是-inf都影响着是否删除重点,平时不可不管,二分必须注意返回值
inline LL sakura(Re k){
if(h==t)return Q[h];
Re l=h,r=t;
while(l<r){
Re mid=l+r>>1,i=Q[mid],j=Q[mid+1];
if(slope(i,j)<k)l=mid+1;
// if( (Y(j) - Y(i)) < k * (X(j) - X(i)) )l=mid+1;//注意是(j)-(i)因为Q[mid+1]>Q[mid]s即j>i即SF[j]>SF[i]即X(j)>X(i),如果是(i)-(j)的话乘过去要变号
else r=mid;
}
return Q[l];
}
int main(){
scanf("%lld%lld",&n,&S);
for(i=1;i<=n;ST[i]+=ST[i-1],SF[i]+=SF[i-1],++i)scanf("%lld%lld",&ST[i],&SF[i]);
Q[++t]=0;
for(i=1;i<=n;++i){
j=sakura(S+ST[i]);
dp[i]=dp[j]+ST[i]*(SF[i]-SF[j])+S*(SF[n]-SF[j]);
while(h<t&&slope(Q[t-1],Q[t])>=slope(Q[t-1],i))--t;//此处取等号作用出现,如果不取等,会WA第12个点
Q[++t]=i;
}
printf("%lld",dp[n]);
}
3.【CDQ/平衡树】
因为暂时没找到 \(X(j)\) 不单调、\(k_0[i]\) 单调的例题,这里直接讲两者均不单调的情况。
如果学习了动态凸包算法,会发现这其实就是套了个板子上去(平衡树代码较毒瘤就不放了)。
\(\text{CDQ}\) 做法也比较显然,但因为递归过程不好描述,直接看代码注释吧。
时间复杂度为 \(O(n\log n)\)。
【Code】
#include<algorithm>
#include<cstring>
#include<cstdio>
#define LD long double
#define LL long long
#define Re register int
#define S2(a) (1ll*(a)*(a))
using namespace std;
const LL N=1e5+3,inf=1e18;
int n,H[N],W[N],Q[N];LL S[N],dp[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
//dp[i]=min(dp[i],dp[j]+(H[i]-H[j])*(H[i]-H[j])+S[i-1]-S[j]);
//dp[i]=dp[j]-2*H[i]*H[j]+H[j]*H[j]+H[i]*H[i]+S[i-1]-S[j]
//(2*H[i]) * H[j] + (dp[i]-S[i-1]-H[i]*H[i]) = (dp[j]+H[j]*H[j]-S[j])
// k * x + b = y
#define X(j) (a[j].x)
#define Y(j) (a[j].y)
struct QAQ{
int k,x,id;LL y;
inline bool operator<(const QAQ &O)const{return x!=O.x?x<O.x:y<O.y;}
}a[N],b[N];
inline bool cmp(QAQ A,QAQ B){return A.k<B.k;}
inline LD slope(Re i,Re j){return X(i)==X(j)?(Y(j)>Y(i)?inf:-inf):(LD)(Y(j)-Y(i))/(X(j)-X(i));}
inline void CDQ(Re L,Re R){
if(L==R){Re j=a[L].id;a[L].y=dp[j]+(LL)H[j]*H[j]-S[j];return;}//此时dp[j]必定已经求出来了,直接算计Y(j)即可
Re mid=L+R>>1,p1=L,p2=mid+1,h=1,t=0;
for(Re i=L;i<=R;++i)a[i].id<=mid?b[p1++]=a[i]:b[p2++]=a[i];//按照i的大小分到左右两边(两边的k0[i]分别递增)
for(Re i=L;i<=R;++i)a[i]=b[i];
CDQ(L,mid);//处理完左边后,左边的X(j)是递增的,此时右边还没处理,所以右边k0[i]是递增的
for(Re i=L;i<=mid;++i){//把左边的点拿出来维护凸包(使用单调队列)
while(h<t&&slope(Q[t-1],Q[t])>=slope(Q[t-1],i))--t;
Q[++t]=i;
}
for(Re i=mid+1,j,id;i<=R;++i){//把右边的点拿来决策(依旧是单调队列)
while(h<t&&slope(Q[h],Q[h+1])<=a[i].k)++h;
if(h<=t)id=a[i].id,j=Q[h],dp[id]=min(dp[id],a[j].y-(LL)a[i].k*a[j].x+S[id-1]+(LL)H[id]*H[id]);
}
CDQ(mid+1,R);//处理完右边后,两边都按照X(j)排好了序
Re w=L-1;p1=L,p2=mid+1;//把两边按照X(j)从小到大归并起来
while(p1<=mid&&p2<=R)b[++w]=a[p1]<a[p2]?a[p1++]:a[p2++];
while(p1<=mid)b[++w]=a[p1++];while(p2<=R)b[++w]=a[p2++];
for(Re i=L;i<=R;++i)a[i]=b[i];
}
int main(){
// freopen("123.txt","r",stdin);
in(n);
for(Re i=1;i<=n;++i)in(H[i]);
for(Re i=1;i<=n;++i)in(W[i]);
for(Re i=1;i<=n;++i)S[i]=S[i-1]+W[i],dp[i]=inf;
for(Re i=1;i<=n;++i)a[i].k=(H[i]<<1),a[i].x=H[i],a[i].id=i;
sort(a+1,a+n+1,cmp);//先按k0[i]排序
dp[1]=0,CDQ(1,n);//注意左边界上的点要单独求
printf("%lld\n",dp[n]);
}
4.【题目链接】
(以此处为分界线,上面都是 \(X(j)\) 与 \(k_0[i]\) 均单调的例子)
-
任务安排 \(3\) \(\text{[SDOI2012] [P5785]}\) \(\text{[Loj10186]}\) \(\text{[Bzoj2726]}\)(\(X(j)\) 单调 \(k_0[i]\) 不单调)
-
高速公路 \(\text{[P3994]}\)(\(X(j)\) 单调 \(k_0[i]\) 不单调。树上转移)
-
购票 \(\text{[NOI2014] [P2305]}\)(\(X(j)\) 单调 \(k_0[i]\) 不单调。树上转移)
-
\(\text{Building Bridges [CEOI2017] [P4655]}\)(\(X(j)\) 与 \(k_0[i]\) 均不单调)
-
货币兑换 \(\text{[NOI2007] [P4027]}\)(\(X(j)\) 与 \(k_0[i]\) 均不单调)
【参考资料】
(本文部分内容摘自以下文章)




 浙公网安备 33010602011771号
浙公网安备 33010602011771号