【题解】Largest Rectangle in a Histogram [SP1805] [POJ2559]
【题解】Largest Rectangle in a Histogram [SP1805] [POJ2559]
【题目描述】
传送： \(Largest\) \(Rectangle\) \(in\) \(a\) \(Histogram\) \([SP1805]\) \([POJ2559]\)
同一水平线上有 \(n\) 个矩形，构成了一个柱状多边形，矩形宽度均为 \(1\)，高度不同。如图：
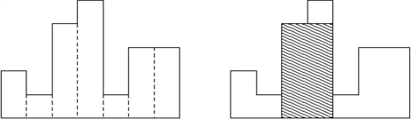
你需要在多边形中框选出一个矩形，使其面积最大，如图阴影部分。
【输入】
每组数据包含一个整数 \(n\)，以及 \(n\) 个整数 \(hi\) 。
结尾以一个单独的 \(0\) 结尾。
【输出】
对于每组数据，直接输出这个最大面积 。
【样例】
输入：
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0
输出：
8
4000
【分析】
有两种解法，递推和单调栈。
【递推】
问题转换：
假定我们选定了某一个矩形的高，那么由这个高所能得到的最大面积，就是从这个矩形的位置出发，看它最多能向左，右两边延伸多远的距离，并且乘以选定的这个高度。
如果我们能预处理出每个点向左右两边能到达的最远距离，那么这个题就 \(so\) \(easy\)。
如何求一个点向左，右延伸所能到达的极限？
对于每一个位置 \(i\)，我们先把它与上一个位置 \(i-1\) 的高度作比较，如果 \(h[i] \leqslant h[i-1]\)，那么 \(i-1\) 的左极限 \(L[i-1]\) 也可作为 \(i\) 的左极限。而如果 \(h[\) \(L[i-1]-1\) \(]\) \(\leqslant h[i]\)，那么 \(L[i]=L[i-1]-1\) 。
右极限求法同上。
【Code】
#include<algorithm>
#include<cstdio>
#define LL long long
using namespace std;
int n,a[100005],l[100005],r[100005];LL s,ans;
int main(){
while(scanf("%d",&n)!=EOF){
if(!n)break;
ans=0;
for(int i=1;i<=n;i++){
scanf("%d",&a[i]);
l[i]=r[i]=i;//左右极限都初始化为它自己
while(l[i]>1&&a[l[i]-1]>=a[i])l[i]=l[l[i]-1];
}
for(int i=n;i;i--)
while(r[i]<n&&a[r[i]+1]>=a[i])r[i]=r[r[i]+1];
for(int i=1;i<=n;i++)//扫描，对每个点进行一次择优
ans=max(ans,(LL)a[i]*(r[i]-l[i]+1));
printf("%lld\n",ans);
}
}
【单调栈】
建立一个栈存储所有矩形的高度和宽度，宽度全部初始化为 \(1\) 。
每当读入一个点 \(i\) 的高度，判断如果它比上一个点 \(i-1\) 低，那么就进行一次假定选择 \(i-1\) 的高度的计算，计算方法就是不停的出栈，并且不断累加弹出的矩形宽度 \(wide\) ，每弹出一个，就用 \(wide\) 乘以这个弹出的矩形的高度，并且与 \(ans\) 进行一次择优。一直弹到当栈顶矩形高小于等于 \(h[i]\) 时，把一个宽度为 \(wide+1\)，高度为 \(h[i]\) 的新矩形入栈。
如果它比上一个高，则直接入栈。
为方便处理最后剩余的矩形，\(把 h[n+1]\) 赋值为一个极大值。
正确性？
而实际上刚刚这样的弹栈边计算计算的方法只计算了每个点在局部所能制造出的面积。只计算每个点的局部最优显然不能得到正确答案，但它对全局所能产生影响的，仅有高度小于等于新矩形高度的下面部分，至于上面的，在以后永远也不会再选到，所以弹出后直接留下宽度送给新矩形即可保留它对全局的影响。
【Code】
#include<algorithm>
#include<cstdio>
int i,n,t,wi,a[100005],Q[100005],W[100005];
long long ans;
int main(){
while(scanf("%d",&n)!=EOF){
if(!n)break;
for(i=1;i<=n;i++)scanf("%d",&a[i]);
ans=a[n+1]=t=0;//提前预处理a[n+1]；清空栈
for(i=1;i<=n+1;i++)
if(a[i]>Q[t])Q[++t]=a[i],W[t]=1;//如果仍保持单调性，则直接入栈
else{
wi=0;
while(t&&a[i]<=Q[t])ans=std::max(ans,(long long)(wi+=W[t])*Q[t--]);
//每弹出一个就计算一下：如果选定当前这个矩形向左最多能获得多大的面积收益
Q[++t]=a[i],W[t]=wi+1;//合并且入栈
}
printf("%lld\n",ans);
}
}
