【题解】Editor [HDU4699]
【题解】Editor [HDU4699]
【题目描述】
有一个维护整数序列的强大编辑器,初始状态为空,下面提供五种不同的操作,给出的总操作次数 \(m \leqslant 1e6\) 。
\(“I,x”:\) 在光标后面添加一个整数 \(x\);
\(“D”:\) 删除光标前面的整数; \([Backspace]\)
\(“L”:\) 光标向左移动一个单位,除非它已在第一个位置; \([←]\)
\(“R”:\) 光标向右移动一个单位,除非它已在最后一个位置; \([→]\)
\(“Q,k”:\) 输出位置在k之前的最大前缀和。
【样例】
输入:
8
I 2
I -1
I 1
Q 3
L
D
R
Q 2
输出:
2
3
【数据范围】
\(1 \leqslant Q \leqslant 1e6\) \(,\) \(\left| x \right| \leqslant 1000\)
【分析】
对顶栈的炒鸡大水题
但毕竟当初花了那么对时间去搞栈,所以还是水写几篇题解吧...
仔细观察一下题目,问题的关键就在于\(“I”\),\(“D”\),即添加和删除,这里我们先换个词,插入(~~啊恩~)和弹出。如果暂时不考虑光标左右移动的情况,那么每次删除的一定是最后一次插入的整数。后进先出,一进一出的动作都在序列尾进行,这不就是个栈么?
那么如何解决光标左右移动的情况呢?
我们可以设置两个栈 \(L\) 和 \(R\),分别表示光标左右两边的所有数字,靠近光标左右两边的数为栈顶,序列首和序列尾为栈底。
对于每一次的操作:
插入\((“I,x”):\)把 \(x\) 丢进 \(L\)。
删除\((“D”):\)弹出 \(L\) 栈顶元素。
左移\((“L”):\)弹出 \(L\) 栈顶元素,并丢进 \(R\)。
右移\((“R”):\)弹出 \(R\) 栈顶元素,并丢进 \(L\)。
模拟一下。。。
当前的状态:
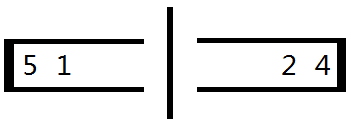
删除操作后的状态:
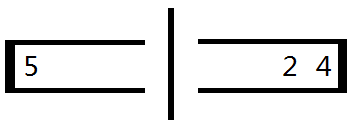
右移操作后的状态:
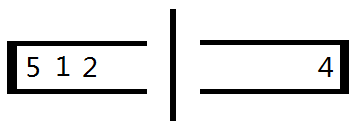
左移操作后的状态:
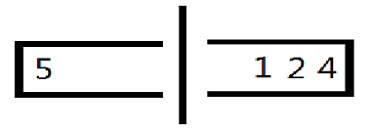
\((“Q,k”)\) 如何查询最大前缀和?
其实很简单,用一个变量 \(sum\) 表示当前位置的前缀和,再开一个数组 \(f[\) \(]\) 保存每个位置前面的最大前缀和。
当 \(L\) 中有元素 \(x\) 插入时,更新 \(sum\) 和 \(f[\) \(]\),当有元素弹出时,只更新 \(sum\) 。
这道题有两种实现方法:\(STL\) 和手写栈。
不过呢,用 \(STL\) 速度慢,代码长......懂我什么意思了吧....
【Code】
【STL】
#include<iostream>
#include<cstdio>
#include<stack>
using namespace std;
const int N=1e6+5;
stack<int> L,R;
int m,x,t,f[N],sum;char a;
inline int Max(int x,int y){return x>y?x:y;}
int main(){
while(scanf("%d",&m)>0){
t=sum=0;//用t表示当前L中的元素个数,同时也是光标左边的位置
while(!L.empty())L.pop();//清空两个栈
while(!R.empty())R.pop();//QAQ,QWQ,QAQ
f[0]=-0x7fffffff;//这个很重要,否则会WA一片
while(m--){
cin>>a;
if(a=='I'){//添加
scanf("%d",&x);
L.push(x);++t;//左边新增一个数x
f[t]=Max(f[t-1],sum+=x);//更新sum,f[tL]
}
else if(a=='D'&&!L.empty())sum-=L.top(),L.pop(),t--;//删除,sum也实时更新
else if(a=='L'&&!L.empty()){//左移
R.push(L.top());//左边减少一个数,放入右边
sum-=L.top();//更新sum
L.pop();t--;
}
else if(a=='R'&&!R.empty()){//右移
L.push(R.top());t++;//右边减少一个数,放入左边
f[t]=Max(f[t-1],sum+=R.top());//更新sum,f[tL]
R.pop();
}
else if(a=='Q')scanf("%d",&x),printf("%d\n",f[x]);//查询
}
}
}
【手写栈】
#include<iostream>
#include<cstdio>
using namespace std;
const int N=1e6+5;
int m,x,tL,tR,L[N],R[N],f[N],sum;char a;
inline int Max(int x,int y){return x>y?x:y;}
int main(){
while(scanf("%d",&m)>0){
tL=tR=sum=0;f[0]=-0x7fffffff;
while(m--){
cin>>a;
if(a=='I'){
scanf("%d",&x);
L[++tL]=x;
f[tL]=Max(f[tL-1],sum+=x);
}
if(a=='R'&&tR){
x=L[++tL]=R[tR--];
f[tL]=Max(f[tL-1],sum+=x);
}
if(a=='Q')scanf("%d",&x),printf("%d\n",f[x]);
if(a=='L'&&tL){sum-=L[tL],R[++tR]=L[tL--];}
if(a=='D'&&tL)sum-=L[tL--];
}
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号