【模板整合计划】数论数学
【模板整合计划】数论数学
一:【数论】
二:【线性代数】
1.【 矩阵快速幂】
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register LL
const int N=103,P=1e9+7;
LL n,K;
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
struct Matrix{
LL a[N][N];
Matrix(){memset(a,0,sizeof(a));}
inline void read(){
for(Re i=1;i<=n;++i)
for(Re j=1;j<=n;++j)
in(a[i][j]);
}
inline void print(){
for(Re i=1;i<=n;puts(""),++i)
for(Re j=1;j<=n;++j)
printf("%lld ",a[i][j]);
}
inline Matrix operator*(const Matrix &O)const{
Matrix ans;
for(Re i=1;i<=n;++i)
for(Re j=1;j<=n;++j)
for(Re k=1;k<=n;++k)
(ans.a[i][j]+=a[i][k]*O.a[k][j]%P)%=P;
return ans;
}
inline Matrix operator*=(Matrix &O){return *this=*this*O;}
}A;
inline Matrix mi(Matrix x,Re k){
if(!k)return x;--k;//矩阵的0次方即为单位矩阵
Matrix s=x;
while(k){
if(k&1)s*=x;
x*=x,k>>=1;
}
return s;
}
int main(){
in(n),in(K),A.read(),mi(A,K).print();
}
2.【高斯消元】
(1).【高斯消元 (Gauss Elimination)】
不会写这种。
(2).【高斯约旦消元 (Gauss-Jordan Elimination)】
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LD double
#define LL long long
#define Re register int
using namespace std;
const int N=103;
int n;LD eps=1e-8,a[N][N];
inline int dcmp(Re a){return a<-eps?-1:(a>eps?1:0);}
inline LD Abs(LD a){return dcmp(a)*a;}
inline void in(Re &x){
Re fu=0;x=0;char ch=getchar();
while(ch<'0'||ch>'9')fu|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=fu?-x:x;
}
int main(){
// freopen("123.txt","r",stdin);
in(n);
for(Re i=1;i<=n;++i)
for(Re j=1;j<=n+1;++j)
scanf("%lf",&a[i][j]);
for(Re j=1;j<=n;++j){
Re w=j;
for(Re i=j+1;i<=n;++i)
if(dcmp(Abs(a[i][j])-Abs(a[w][j]))>0)w=i;
for(Re k=1;k<=n+1;++k)swap(a[j][k],a[w][k]);
if(!dcmp(a[j][j]))return !puts("No Solution");
for(Re i=1;i<=n;++i)
if(i!=j){
LD tmp=a[i][j]/a[j][j];
for(Re k=j;k<=n+1;++k)a[i][k]-=a[j][k]*tmp;
}
}
for(Re i=1;i<=n;++i)printf("%.2lf\n",a[i][n+1]/a[i][i]);
}
3.【线性基】
(1).【线性基】
#include<algorithm>
#include<cstdio>
#define LL long long
#define Re register LL
using namespace std;
const int N=55;
LL n,x,ans,p[N];
inline void in(Re &x){
Re fu=0;x=0;char ch=getchar();
while(ch<'0'||ch>'9')fu|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=fu?-x:x;
}
inline void insert(Re x){
for(Re i=50;i>=0;--i)
if((x>>i)&1){
if(!p[i]){p[i]=x;break;}
x^=p[i];
}
}
int main(){
// freopen("123.txt","r",stdin);
in(n);
for(Re i=1;i<=n;++i)in(x),insert(x);
for(Re i=50;i>=0;--i)ans=max(ans,ans^p[i]);
printf("%lld\n",ans);
}
(2).【前缀线性基】
【模板】\(\text{Ivan and Burgers}\) \(\text{[CF1100F]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=5e5+3,logN=20,inf=2e9;
int n,x,y,T;
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
struct JI{
int p[logN+1],ip[logN+1];JI(){memset(p,0,sizeof(p));}
inline void insert(Re x,Re id){
for(Re i=logN;i>=0;--i)
if((x>>i)&1){
if(!p[i]){p[i]=x,ip[i]=id;break;}
if(ip[i]<id)swap(p[i],x),swap(ip[i],id);//注意这里要swap,不能直接赋值
x^=p[i];
}
}
inline int ask(Re L){
Re ans=0;
for(Re i=logN;i>=0;--i)if(ip[i]>=L)ans=max(ans,ans^p[i]);
return ans;
}
}A[N],S[N];
int main(){
// freopen("456.txt","r",stdin);
in(n);
for(Re i=1;i<=n;++i)in(x),S[i]=S[i-1],S[i].insert(x,i);
in(T);
while(T--)in(x),in(y),printf("%d\n",S[y].ask(x));
}
(3).【线性基合并】
幸运数字 \(\text{[SCOI2016] [P3292]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#define LL long long
#define Re register LL
using namespace std;
const LL N=2e4+3,M=2e5+3,inf=2e18,logN=14;
LL n,m,o,x,y,T,A[N],head[N];
struct QAQ{LL to,next;}a[N<<1];
inline void add(Re x,Re y){a[++o].to=y,a[o].next=head[x],head[x]=o;}
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
struct JI{
LL p[61];JI(){memset(p,0,sizeof(p));}
inline void insert(Re x){
for(Re i=60;i>=0;--i)
if((x>>i)&1){
if(!p[i]){p[i]=x;break;}
x^=p[i];
}
}
inline void merge(JI O){
for(Re i=60;i>=0;--i)if(O.p[i])insert(O.p[i]);
}
inline LL ask(){
Re ans=0;
for(Re i=60;i>=0;--i)ans=max(ans,ans^p[i]);
return ans;
}
};
struct LCA{
LL deep[N],fa[N][15],ant[N][15];JI dp[N][15];
inline void dfs(Re x,Re fa){
deep[x]=deep[ant[x][0]=fa]+1,dp[x][0].insert(A[fa]);
for(Re j=1;(1<<j)<=deep[x];++j)ant[x][j]=ant[ant[x][j-1]][j-1],dp[x][j]=dp[x][j-1],dp[x][j].merge(dp[ant[x][j-1]][j-1]);
for(Re i=head[x];i;i=a[i].next)if(a[i].to!=fa)dfs(a[i].to,x);
}
inline JI ask(Re x,Re y){
JI Ans;Ans.insert(A[x]),Ans.insert(A[y]);
if(deep[x]<deep[y])swap(x,y);
for(Re i=logN;i>=0;--i)if(deep[ant[x][i]]>=deep[y])Ans.merge(dp[x][i]),x=ant[x][i];
if(x==y)return Ans;
for(Re i=logN;i>=0;--i)if(ant[x][i]!=ant[y][i])Ans.merge(dp[x][i]),Ans.merge(dp[y][i]),x=ant[x][i],y=ant[y][i];
Ans.merge(dp[x][0]);
return Ans;
}
}T1;
int main(){
// freopen("lucky.in","r",stdin);
// freopen("lucky.out","w",stdout);
in(n),in(T),m=n-1;
for(Re i=1;i<=n;++i)in(A[i]);
while(m--)in(x),in(y),add(x,y),add(y,x);
T1.dfs(1,0);
while(T--)in(x),in(y),printf("%lld\n",T1.ask(x,y).ask());
}
三:【组合数学】
1.【组合数】
(1).【n^2 递推】
inline void get_C(Re N){
for(Re i=0;i<=N;++i)C[0][i]=C[i][i]=1;
for(Re i=1;i<=N;++i)
for(Re j=1;j<i;++j)
C[j][i]=(C[j-1][i-1]+C[j][i-1])%P;
}
(2).【n^2 记搜】
inline int C(Re m,Re n){
if(m>n)return 0;
if(!m||m==n)return C_[m][n]=1;
if(C_[m][n])return C_[m][n];
return C_[m][n]=(C(m,n-1)+C(m-1,n-1))%P;
}
2.【卢卡斯定理 (Lucas)】
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=1e5+3;
int n,m,P,T,jc[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
inline int C(Re m,Re n){
return m>n?0:(LL)jc[n]*inv(jc[m])%P*inv(jc[n-m])%P;
}
inline int Lucas(Re m,Re n){
return m==0?1:(LL)Lucas(m/P,n/P)*C(m%P,n%P)%P;
}
int main(){
// freopen("123.txt","r",stdin);
in(T);
while(T--){
in(n),in(m),in(P),jc[0]=1;
for(Re i=1;i<=P-1;++i)jc[i]=(LL)jc[i-1]*i%P;
printf("%d\n",Lucas(n,n+m));
}
}
3.【扩展卢卡斯定理 (ExLucas)】
还不会,先咕着。
4.【卡特兰数 (Catalan)】
(1).【质因数分解求法 (取模)】
【模板】有趣的数列 \(\text{[HNOI2009] [P3200]}\)
#include<cstdio>
#define LL long long
#define Re register LL
const int N=1e6+3;
LL n,P,cnt,pri[N],pan[N<<1];
inline void get_pri(Re N){
for(Re i=2;i<=N;++i){
if(!pan[i])pri[++cnt]=i;
for(Re j=1;j<=cnt&&i*pri[j]<=N;++j)pan[i*pri[j]]=1;
}
}
inline LL Catalan(Re n){
Re ans=1;cnt=0;get_pri(n<<1);
for(Re i=1;i<=cnt;i++){
Re x=pri[i],t=0;
while(x<=2*n){t+=2*n/x-n/x-(n+1)/x;x*=pri[i];}
while(t--)(ans*=pri[i])%=P;
}
return ans%P;
}
int main(){
scanf("%lld%lld",&n,&P);
printf("%lld",Catalan(n));
}
(2).【质因数分解求法 (高精度)】
【模板】火车进出栈问题 \(\text{[CH1102]}\)
#include<cstdio>
#define R register int
int n,t,x,len,ans[100000],pan[120005];
void cf(int x){
R i,j;
for(i=1;i<=len;i++)ans[i]*=x;
len+=6;
for(i=1;i<=len;i++)ans[i+1]+=ans[i]/10,ans[i]%=10;
while(!ans[len])len--;
}
int main(){
scanf("%d",&n);R i,j;len=ans[1]=1;
for(i=2;i<=2*n;i++)
if(pan[i]==0){
x=i;t=0;
while(x<=2*n){t+=2*n/x-n/x-(n+1)/x;x*=i;}
while(t--)cf(i);
for(j=i;j<=2*n/i;j++)pan[i*j]=1;
}
for(i=len;i>=1;i--)printf("%d",ans[i]);
}
5.【第一类斯特林数】
(1).【n^2 递推】
inline void get_stiring(Re N){
for(Re i=0;i<=N;++i)s[i][i]=1;
for(Re i=1;i<=N;++i)
for(Re j=1;j<i;++j)
s[j][i]=s[j-1][i-1]+(LL)(i-1)*s[j][i-1]%P;
}
(2).【行(两只 log 暴力分治 NTT)】
【模板】第一类斯特林数 ·行 \(\text{[P5408]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LD double
#define LL long long
#define Re register int
using namespace std;
const int N=262144+3,P=167772161,G=3;
int n,m,invn,invG,tr[N],A[20][N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
inline void NTT(Re *f,Re n,Re op){
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1)
for(Re st=0,len=p>>1,w1=mi(op?invG:G,(P-1)/p);st<n;st+=p)
for(Re i=st,base=1;i<=st+len-1;++i){
Re tmp=(LL)base*f[i+len]%P;
f[i+len]=(f[i]-tmp+P)%P,f[i]=(f[i]+tmp)%P,base=(LL)base*w1%P;
}
}
inline void times(Re *f,Re n,Re *g,Re m){
Re n_=n,m_=m;
for(m+=n,n=1;n<=m;n<<=1);
for(Re i=n_+1;i<=n;++i)f[i]=0;//奇怪的初始化
for(Re i=m_+1;i<=n;++i)g[i]=0;//奇怪的初始化
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P;
NTT(f,n,1);
for(Re i=0,invn=inv(n);i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
inline void CDQ(Re L,Re R,Re deep){
if(L==R){A[deep][0]=L,A[deep][1]=1;return;}
Re mid=L+R>>1;
CDQ(L,mid,deep+1);
for(Re i=0;i<=mid-L+1;++i)A[deep][i]=A[deep+1][i];//存左边
CDQ(mid+1,R,deep+1);
times(A[deep],mid-L+1,A[deep+1],R-mid);//左边乘右边
}
int s[N];
inline void get_Stirling(Re n){
invG=inv(G),CDQ(0,n-1,0);
for(Re i=0;i<=n;++i)s[i]=A[0][i];
}
int main(){
// freopen("123.txt","r",stdin);
in(n),get_Stirling(n);
for(Re i=0;i<=n;++i)printf("%d ",s[i]);
}
(3).【行(一只 log 优化倍增 NTT)】
【模板】第一类斯特林数 ·行 \(\text{[P5408]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LD double
#define LL long long
#define Re register int
using namespace std;
const int N=262144+3,P=167772161,G=3;
int n,m,invn,invG,f[N],g[N],h[N],p[N],tr[N],jc[N],invjc[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
inline void NTT(Re *f,Re n,Re op){
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1)
for(Re st=0,len=p>>1,w1=mi(op?invG:G,(P-1)/p);st<n;st+=p)
for(Re i=st,base=1;i<=st+len-1;++i){
Re tmp=(LL)base*f[i+len]%P;
f[i+len]=(f[i]-tmp+P)%P,f[i]=(f[i]+tmp)%P,base=(LL)base*w1%P;
}
}
inline void times(Re *f,Re n,Re *g,Re m){
Re n_=n,m_=m;
for(m+=n,n=1;n<=m;n<<=1);
for(Re i=n_+1;i<=n;++i)f[i]=0;//奇怪的初始化
for(Re i=m_+1;i<=n;++i)g[i]=0;//奇怪的初始化
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P;
NTT(f,n,1);
for(Re i=0,invn=inv(n);i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
inline void xplus(Re *f,Re *F,Re n,Re c){
for(Re i=0;i<=n;++i)h[i]=(LL)F[i]*jc[i]%P;
for(Re i=0,Mi=1;i<=n;++i)p[n-i]=(LL)Mi*invjc[i]%P,Mi=(LL)Mi*c%P;
times(h,n,p,n);
for(Re i=0;i<=n;++i)f[i]=(LL)h[n+i]*invjc[i]%P;
}
inline void sakura(Re *f,Re n){
if(n==1){f[0]=0,f[1]=1;return;}//(x+0)
if(n&1){
sakura(f,n-1);
for(Re i=n;i;--i)f[i]=((LL)f[i]*(n-1)%P+f[i-1])%P;
f[0]=(LL)f[0]*(n-1)%P;
}
else sakura(f,n>>1),xplus(g,f,n>>1,n>>1),times(f,n>>1,g,n>>1);
}
int s[N];
inline void get_Stirling(Re n){
invjc[1]=invjc[0]=jc[0]=1,invG=inv(G);//注意inv[jc[0]]=1
if(n==0){s[0]=1;return;}
for(Re i=1;i<=n;++i)jc[i]=(LL)jc[i-1]*i%P;
for(Re i=2;i<=n;++i)invjc[i]=(LL)invjc[P%i]*(P-P/i)%P;
for(Re i=2;i<=n;++i)invjc[i]=(LL)invjc[i]*invjc[i-1]%P;
sakura(s,n);
}
int main(){
// freopen("123.txt","r",stdin);
in(n),get_Stirling(n);
for(Re i=0;i<=n;++i)printf("%d ",s[i]);
}
(4).【列】
【模板】第一类斯特林数 ·列 \(\text{[P5409]}\)
还不会,先咕着。
6.【第二类斯特林数】
(1).【n^2 递推】
inline void get_Stiring(Re N){
for(Re i=0;i<=N;++i)S[i][i]=1;
for(Re i=1;i<=N;++i)
for(Re j=1;j<i;++j)
S[j][i]=S[j-1][i-1]+(LL)j*S[j][i-1]%P;
}
(2).【行】
【模板】第二类斯特林数 · 行 \(\text{[P5395]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=524288+3,P=167772161,G=3;
int n,invG,f[N],g[N],tr[N],jc[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
inline void NTT(Re *f,Re n,Re op){
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1)
for(Re st=0,len=p>>1,w1=mi(op?invG:G,(P-1)/p);st<n;st+=p)
for(Re i=st,base=1;i<=st+len-1;++i){
Re tmp=(LL)f[i+len]*base%P;
f[i+len]=(f[i]-tmp+P)%P,(f[i]+=tmp)%=P,base=(LL)base*w1%P;
}
}
inline void sakura(Re *f,Re n,Re *g,Re m){
for(m+=n,n=1;n<=m;n<<=1);
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P;
NTT(f,n,1);
for(Re i=0,invn=inv(n);i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
int S[N];
inline void get_Stirling(Re n){
jc[0]=1,invG=inv(G);
for(Re i=1;i<=n;++i)jc[i]=(LL)jc[i-1]*i%P;
for(Re i=0;i<=n;++i)f[i]=(LL)inv(jc[i])*((i&1)?P-1:1)%P,g[i]=(LL)mi(i,n)*inv(jc[i])%P;
sakura(f,n,g,n);
for(Re i=0;i<=n;++i)S[i]=f[i];
}
int main(){
// freopen("123.txt","r",stdin);
in(n),get_Stirling(n);
for(Re i=0;i<=n;++i)printf("%d ",S[i]);
}
(3).【列】
【模板】第二类斯特林数 · 列 \(\text{[P5396]}\)
还不会,先咕着。
7.【贝尔数】
【模板】 \(\text{Symmetric and Transitive}\) \(\text{[CF568B]}\)
(1).【n^2 递推】
inline void get_Bell(Re N){
B[0]=1,get_C(N);
for(Re i=1;i<=N;++i)
for(Re j=0;j<=i-1;++j)
(B[i]+=(LL)C[j][i-1]*B[j]%P)%=P;
}
inline void get_Bell_(Re N){
B[0]=1,get_Stiring(N);
for(Re i=1;i<=N;++i)
for(Re j=1;j<=i;++j)
(B[i]+=S[j][i])%=P;
}
8.【康托展开】
#include<cstdio>
#define LL long long
const int N=1e6+5,P=998244353;
int n,i,ans,a[N],g[N],C[N],jc[N]={1};
inline void add(int x){while(x<=n)++C[x],x+=x&-x;}
inline int ask(int x){
int ans=0;
while(x)ans+=C[x],x-=x&-x;
return ans;
}
int main(){
scanf("%d",&n);
for(i=1;i<=n;++i)scanf("%d",&a[i]);
for(i=n;i;--i)g[i]=ask(a[i]-1),add(a[i]);
for(i=1;i<=n;++i)jc[i]=(LL)jc[i-1]*i%P;
for(i=1;i<=n;++i)(ans+=(LL)g[i]*jc[n-i]%P)%=P;
printf("%d",ans+1);
}
9.【Polya 定理】
.png)
.png)
【模板】\(\text{Polya}\) 定理 \(\text{[P4980]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=1e6+3,P=1e9+7;
int n,T,pri[N/3];bool pan[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
inline int phi(Re x){
Re ans=x;
for(Re i=2;i*i<=x;i++)
if(x%i==0){
ans/=i,ans*=i-1;
while(x%i==0)x/=i;
}
if(x>1)ans/=x,ans*=x-1;
return ans;
}
int main(){
// freopen("123.txt","r",stdin);
in(T);
while(T--){
in(n);Re ans=0;
for(Re i=1;i*i<=n;++i)
if(n%i==0){
(ans+=(LL)mi(n,i-1)*phi(n/i)%P)%=P;
if(i!=n/i)(ans+=(LL)mi(n,n/i-1)*phi(i)%P)%=P;
}
printf("%d\n",ans);
}
}
四:【多项式全家桶】
1.【多项式乘法】
【模板】多项式乘法(\(\text{FFT}\))\(\text{[P3803]}\)
(1).【快速傅里叶变换 / FFT (Fast Fourier Transform)】
#include<algorithm>
#include<cstdio>
#include<cmath>
#define LD double
#define LL long long
#define Re register int
using namespace std;
const int N=2097152+3;
const LD Pi=acos(-1);
int n,m,tr[N];
inline void in(Re &x){
Re fu=0;x=0;char ch=getchar();
while(ch<'0'||ch>'9')fu|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=fu?-x:x;
}
struct CP{
LD x,y;CP(LD X=0,LD Y=0){x=X,y=Y;}
inline CP operator+(const CP &O)const{return CP(x+O.x,y+O.y);}
inline CP operator-(const CP &O)const{return CP(x-O.x,y-O.y);}
inline CP operator*(const CP &O)const{return CP(x*O.x-y*O.y,x*O.y+y*O.x);}//(ac-bd,bc+ad)
inline CP operator/(const CP &O)const{
LD tmp=O.x*O.x+O.y*O.y;//tmp=c^2+d^2
return CP((x*O.x+y*O.y)/tmp,(y*O.x-x*O.y)/tmp);//( (ac+bd)/tmp,(bc-ad)/tmp )
}
inline CP operator*=(const CP &O){return *this=*this*O;}
}f[N],g[N];
inline void FFT(CP *f,Re n,Re op){//op=0:DFT, op=1:IDFT
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1){
Re len=p>>1;CP w1(cos(2*Pi/p),sin(2*Pi/p));
if(op)w1.y*=-1;
for(Re st=0;st<n;st+=p){
CP base(1,0);
for(Re i=st;i<=st+len-1;++i){
CP tmp=base*f[len+i];
f[len+i]=f[i]-tmp,f[i]=f[i]+tmp,base*=w1;
}
}
}
}
inline void times(CP *f,Re n,CP *g,Re m){
for(m+=n,n=1;n<=m;n<<=1);
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
FFT(f,n,0),FFT(g,n,0);
for(Re i=0;i<n;++i)f[i]*=g[i];
FFT(f,n,1);
for(Re i=0;i<=m;++i)f[i].x/=n;
}
int main(){
// freopen("123.txt","r",stdin);
in(n),in(m);
for(Re i=0;i<=n;++i)scanf("%lf",&f[i].x);
for(Re i=0;i<=m;++i)scanf("%lf",&g[i].x);
times(f,n,g,m);
for(Re i=0;i<=n+m;++i)printf("%d ",(int)(f[i].x+0.5));
}
(2).【快速数论变换 / NTT (Number Theoretic Transform)】
#include<algorithm>
#include<cstdio>
#include<cmath>
#define LL long long
#define Re register int
using namespace std;
const int N=2097152+3,P=998244353,G=3;
int n,m,invn,invG,f[N],g[N],tr[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
inline void NTT(Re *f,Re n,Re op){
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1){
Re len=p>>1,w1=mi(op?invG:G,(P-1)/p);
for(Re st=0;st<n;st+=p)
for(Re i=st,base=1;i<=st+len-1;++i){
Re tmp=(LL)base*f[len+i]%P;
f[len+i]=(f[i]-tmp+P)%P,(f[i]+=tmp)%=P,base=(LL)base*w1%P;
}
}
}
inline void times(Re *f,Re n,Re *g,Re m){
for(m+=n,n=1;n<=m;n<<=1);invn=inv(n),invG=inv(G);
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P;
NTT(f,n,1);
for(Re i=0;i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
int main(){
// freopen("123.txt","r",stdin);
in(n),in(m);
for(Re i=0;i<=n;++i)in(f[i]);
for(Re i=0;i<=m;++i)in(g[i]);
times(f,n,g,m);
for(Re i=0;i<=n+m;++i)printf("%d ",f[i]);
}
(3).【字符串匹配】
【模板】 \(\text{KMP}\) 字符串匹配 \(\text{[P3375]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<queue>
#define Re register int
#define LL long long
using namespace std;
const int N=1048576+3,P=998244353,G=3;
int n,m,ans,invG,f[N],g[N],tr[N],S1[N],S2[N],PA[N],nex[N];char A[N],B[N];
inline void in(Re &x){
int fu=0;x=0;char c=getchar();
while(c<'0'||c>'9')fu|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=fu?-x:x;
}
inline void get_next(){
for(Re i=2,j=0;i<=m;++i){
while(j&&B[i]!=B[j+1])j=nex[j];
if(B[i]==B[j+1])++j;nex[i]=j;
}
for(Re i=1;i<=m;++i)printf("%d ",nex[i]);
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
inline void NTT(Re *f,Re n,Re op){
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1){
Re len=p>>1,w1=mi(op?invG:G,(P-1)/p);
for(Re st=0;st<n;st+=p)
for(Re j=st,base=1;j<=st+len-1;++j){
Re tmp=(LL)base*f[j+len]%P;
f[j+len]=(f[j]-tmp+P)%P,(f[j]+=tmp)%=P;
base=(LL)base*w1%P;
}
}
}
inline void sakura(Re *f,Re n,Re *g,Re m){
for(m=n+1,n=1;n<=m;n<<=1);Re invn=inv(n);//循环卷积优化
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P;
NTT(f,n,1);
for(Re i=0;i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
int main(){
// freopen("123.txt","r",stdin);
scanf("%s%s",A+1,B+1),invG=inv(G);
n=strlen(A+1),m=strlen(B+1);
for(Re i=1;i<=n;++i)f[i]=A[n-i+1]-'A'+1,S1[i]=S1[i-1]+f[i]*f[i];
for(Re i=1;i<=m;++i)g[i]=B[i]-'A'+1,S2[i]=S2[i-1]+g[i]*g[i];
sakura(f,n,g,m);
for(Re i=m;i<=n;++i)PA[n-i+1]=((S1[i]-S1[i-m]+S2[m])%P-2*f[i+1]%P+P)%P;
for(Re i=1;i<=n-m+1;++i)if(PA[i]==0)printf("%d\n",i);
get_next();
}
2.【分治 FFT / NTT】
【模板】分治 \(\text{FFT}\) \(\text{[P4721]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LD double
#define LL long long
#define Re register int
using namespace std;
const int N=131072+3,P=998244353,G=3;
int n,m,invn,invG,f[N],g[N],A[N],tr[N],ans[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
inline void NTT(Re *f,Re n,Re op){
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1){
Re len=p>>1,w1=mi(op?invG:G,(P-1)/p);
for(Re st=0;st<n;st+=p)
for(Re i=st,base=1;i<=st+len-1;++i){
Re tmp=(LL)base*f[i+len]%P;
f[i+len]=(f[i]-tmp+P)%P;
f[i]=(f[i]+tmp)%P;
base=(LL)base*w1%P;
}
}
}
inline void times(Re *f,Re n,Re *g,Re m){
for(n=1;n<=m;n<<=1);//循环卷积优化
for(Re i=m+1;i<=n;++i)f[i]=g[i]=0;//初始化
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P;
NTT(f,n,1);
for(Re i=0,invn=inv(n);i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
inline void CDQ(Re L,Re R){
if(L==R)return;
Re mid=L+R>>1;CDQ(L,mid);
for(Re i=L;i<=R;++i)g[i-L]=A[i-L];
for(Re i=L;i<=mid;++i)f[i-L]=ans[i];
for(Re i=mid+1;i<=R;++i)f[i-L]=0;
times(f,mid-L,g,R-L);
for(Re i=mid+1;i<=R;++i)(ans[i]+=f[i-L])%=P;
CDQ(mid+1,R);
}
int main(){
// freopen("123.txt","r",stdin);
in(n),invG=inv(G);
for(Re i=1;i<n;++i)in(A[i]);
ans[0]=1,CDQ(0,n-1);
for(Re i=0;i<n;++i)printf("%d ",ans[i]);
}
3.【位运算卷积】
(1).【快速沃尔什变换 / FWT (Fast Walsh-Hadamard Transform)】
【模板】快速沃尔什变换(\(\text{FWT}\))\(\text{[P4717]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LD double
#define LL long long
#define Re register int
using namespace std;
const int N=131072+3,P=998244353;
int n,m,inv2,A[N],B[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int inv(Re x){
Re s=1,k=P-2;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
int id,f[N],g[N];
inline void FWT(Re *f,Re n,Re op){
for(Re p=2;p<=n;p<<=1)
for(Re st=1,len=p>>1;st<n;st+=p)
for(Re j=st;j<=st+len-1;++j)
if(id==1)(f[j+len]+=(op?P-f[j]:f[j]))%=P;
else if(id==2)(f[j]+=(op?P-f[j+len]:f[j+len]))%=P;
else{
Re g0=f[j],g1=f[j+len];
f[j]=(g0+g1)%P,f[j+len]=(g0-g1+P)%P;
if(op)f[j]=(LL)f[j]*inv2%P,f[j+len]=(LL)f[j+len]*inv2%P;
}
}
inline void sakura(Re *A,Re *B,Re n,Re id_){
for(Re i=1;i<=n;++i)f[i]=A[i],g[i]=B[i];id=id_;
FWT(f,n,0),FWT(g,n,0);
for(Re i=1;i<=n;++i)f[i]=(LL)f[i]*g[i]%P;
FWT(f,n,1);
for(Re i=1;i<=n;++i)printf("%d ",f[i]);puts("");
}
int main(){
// freopen("123.txt","r",stdin);
in(n),n=(1<<n),inv2=inv(2);
for(Re i=1;i<=n;++i)in(A[i]);
for(Re i=1;i<=n;++i)in(B[i]);
sakura(A,B,n,1),sakura(A,B,n,2),sakura(A,B,n,3);
}
(2).【快速莫比乌斯变换 / FMT (Fast Mobius Transform)】
还不会,先咕着。
4.【子集卷积】
(1).【快速子集变换 / FST (FST Subset Transform)】
还不会,先咕着。
5.【拉格朗日插值】
(1).【x 从 0 到 n 不连续】
【模板】 拉格朗日插值 \(\text{[P4781]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=2003+3,P=998244353;
inline void in(Re &x){
int f=0;x=0;char ch=getchar();
while(ch<'0'||ch>'9')f|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int Inv(Re x){return mi(x,P-2);}
int ff[N],gg[N];
inline void mul(Re *f,Re n,Re a0,Re *g){//乘以(x+a0)
for(Re i=0;i<=n;++i)ff[i]=f[i];
g[0]=(LL)a0*ff[0]%P;for(Re i=1;i<=n+1;++i)g[i]=((LL)a0*ff[i]%P+ff[i-1])%P;
}
inline void div(Re *g,Re n,Re a0,Re *f){//除以(x+a0)
for(Re i=0;i<=n;++i)gg[i]=g[i];
f[n-1]=gg[n];for(Re i=n-2;i>=0;--i)f[i]=(gg[i+1]-(LL)a0*f[i+1]%P+P)%P;
}
int fi[N],fmul[N];
inline void Lagrange(Re *x,Re *y,Re n,Re *F){//拉格朗日插值(x不连续)
fmul[0]=P-x[0],fmul[1]=1;
for(Re i=1;i<=n;++i)mul(fmul,i,P-x[i],fmul);
for(Re i=0;i<=n-1;++i)F[i]=0;
for(Re i=0;i<=n;++i){
Re tmp=1;
for(Re j=0;j<=n;++j)if(i!=j)tmp=(LL)tmp*(x[i]-x[j]+P)%P;
tmp=(LL)y[i]*Inv(tmp)%P;
div(fmul,n+1,P-x[i],fi);
for(Re i=0;i<=n;++i)(F[i]+=(LL)tmp*fi[i]%P)%=P;
}
}
int n,X,ans,x[N],y[N],F[N];
int main(){
// freopen("123.txt","r",stdin);
in(n),in(X),--n;
for(Re i=0;i<=n;++i)in(x[i]),in(y[i]);
Lagrange(x,y,n,F);
for(Re i=0,tmp=1;i<=n;++i)(ans+=(LL)F[i]*tmp%P)%=P,tmp=(LL)tmp*X%P;
printf("%d\n",ans);
}
(2).【x 从 0 到 n 连续】
【模板】 拉格朗日插值 \(\text{2 [P5667]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=1048576+3,P=998244353,G=3;
int jc[N],inv[N],invjc[N];
inline void in(Re &x){
int f=0;x=0;char ch=getchar();
while(ch<'0'||ch>'9')f|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int Inv(Re x){return mi(x,P-2);}
int invG,tr[N];
inline void NTT(Re *f,Re n,Re op){
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1){
Re len=p>>1,w1=mi(op?invG:G,(P-1)/p);
for(Re st=0;st<n;st+=p)
for(Re i=st,base=1;i<=st+len-1;++i){
Re tmp=(LL)base*f[len+i]%P;
f[len+i]=(f[i]-tmp+P)%P,(f[i]+=tmp)%=P,base=(LL)base*w1%P;
}
}
}
inline void times(Re *f,Re n,Re *g,Re m){
for(m+=n,n=1;n<=m;n<<=1);invG=Inv(G);
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P;
NTT(f,n,1);Re invn=Inv(n);
for(Re i=0;i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
int n,m,y[N],f[N],g[N],F[N];
int main(){
// freopen("123.txt","r",stdin);
in(n),in(m),jc[0]=jc[1]=inv[1]=invjc[0]=invjc[1]=1;
for(Re i=2;i<=n;++i)inv[i]=(LL)inv[P%i]*(P-P/i)%P,jc[i]=(LL)jc[i-1]*i%P,invjc[i]=(LL)invjc[i-1]*inv[i]%P;
for(Re i=0;i<=n;++i)in(y[i]),g[i]=(LL)y[i]*((n-i&1)?P-1:1)%P*invjc[i]%P*invjc[n-i]%P;
for(Re i=0;i<=(n<<1);++i)f[i]=Inv(m-n+i);
times(f,n<<1,g,n);Re tmp=1;
for(Re i=m-n;i<=m;++i)tmp=(LL)tmp*i%P;
for(Re i=0;i<=n;tmp=(LL)tmp*Inv(m-n+i)%P,++i,tmp=(LL)tmp*(m+i)%P)F[i]=(LL)tmp*f[n+i]%P;
for(Re i=m;i<=m+n;++i)printf("%d ",F[i-m]);
}
6.【多项式求逆】
(1).【两只 log 暴力分治 NTT】
【模板】 多项式乘法逆 \(\text{[P4238]}\)
#include<algorithm>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=262144+3,P=998244353,G=3;
int n,A[N],B[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
int invG,tr[N];
inline void NTT(Re *f,Re n,Re op){
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1)
for(Re st=0,len=p>>1,w1=mi(op?invG:G,(P-1)/p);st<n;st+=p)
for(Re j=st,base=1;j<=st+len-1;++j){
Re tmp=(LL)base*f[j+len]%P;
f[j+len]=(f[j]-tmp+P)%P,(f[j]+=tmp)%=P,base=(LL)base*w1%P;
}
}
inline void times(Re *f,Re n,Re *g,Re m){
for(n=1;n<=m;n<<=1);invG=inv(G);
for(Re i=m+1;i<n;++i)f[i]=g[i]=0;
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P;
NTT(f,n,1);Re invn=inv(n);
for(Re i=0;i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
int f[N],g[N],c[N],ans[N];
inline void CDQ(Re L,Re R){
if(L==R)return;
Re mid=L+R>>1;CDQ(L,mid);
for(Re i=L;i<=R;++i)g[i-L]=c[i-L];
for(Re i=L;i<=mid;++i)f[i-L]=ans[i];
for(Re i=mid+1;i<=R;++i)f[i-L]=0;
times(f,mid-L,g,R-L);
for(Re i=mid+1;i<=R;++i)(ans[i]+=f[i-L])%=P;
CDQ(mid+1,R);
}
inline void polyinv(Re *a,Re n,Re *b){
Re tmp=inv(a[0]);c[0]=0;
for(Re i=1;i<=n;++i)c[i]=(LL)(P-a[i])*tmp%P;
ans[0]=tmp,CDQ(0,n);
for(Re i=0;i<=n;++i)b[i]=ans[i];
}
int main(){
// freopen("123.txt","r",stdin);
in(n),--n;
for(Re i=0;i<=n;++i)in(A[i]),A[i]%=P;
polyinv(A,n,B);
for(Re i=0;i<=n;++i)printf("%d ",B[i]);
}
(2).【一只 log 优化倍增 NTT】
【模板】 多项式乘法逆 \(\text{[P4238]}\)
#include<algorithm>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=262144+3,P=998244353,G=3;
int n,A[N],B[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
int invG,tr[N];
inline void NTT(Re *f,Re n,Re op){
for(Re i=0;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1)
for(Re st=0,len=p>>1,w1=mi(op?invG:G,(P-1)/p);st<n;st+=p)
for(Re j=st,base=1;j<=st+len-1;++j){
Re tmp=(LL)base*f[j+len]%P;
f[j+len]=(f[j]-tmp+P)%P,(f[j]+=tmp)%=P,base=(LL)base*w1%P;
}
}
inline void times(Re *f,Re n,Re *g,Re m,Re op=0){
Re n_=n,m_=m;
for(m+=n,n=1;n<=m;n<<=1);invG=inv(G);
for(Re i=n_+1;i<n;++i)f[i]=0;
for(Re i=m_+1;i<n;++i)g[i]=0;
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P*(op?g[i]:1)%P;
NTT(f,n,1);Re invn=inv(n);
for(Re i=0;i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
int f[N],g[N];
inline void polyinv(Re *a,Re n,Re *b){
if(n==0){b[0]=inv(a[0]);return;}
polyinv(a,n>>1,b);
for(Re i=0;i<=n;++i)f[i]=a[i],g[i]=b[i];
times(f,n,g,n,1);
for(Re i=0;i<=n;++i)b[i]=(2*b[i]%P-f[i]+P)%P;
}
int main(){
// freopen("123.txt","r",stdin);
in(n),--n;
for(Re i=0;i<=n;++i)in(A[i]),A[i]%=P;
polyinv(A,n,B);
for(Re i=0;i<=n;++i)printf("%d ",B[i]);
}
7.【多项式快速幂】
(1).【两只 log 暴力 NTT】
【模板】 多项式快速幂 \(\text{[P5245]}\)
#include<algorithm>
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=262144+3,P=998244353,G=3,phi=P-1;
inline void in(Re &x){
int f=0;x=0;char ch=getchar();
while(ch<'0'||ch>'9')f|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=f?-x:x;
}
inline int in_(){
int f=0;LL x=0;char ch=getchar();
while(ch<'0'||ch>'9')ch=getchar();
while(ch>='0'&&ch<='9')x=x*10+(ch^48),x%=P,ch=getchar();
return x;
}
inline int mi(Re x,Re k){
Re s=1;
while(k){
if(k&1)s=(LL)s*x%P;
x=(LL)x*x%P,k>>=1;
}
return s;
}
inline int inv(Re x){return mi(x,P-2);}
int invG,tr[N];
inline void NTT(Re *f,Re n,Re op){
for(Re i=1;i<n;++i)if(i<tr[i])swap(f[i],f[tr[i]]);
for(Re p=2;p<=n;p<<=1)
for(Re st=0,len=p>>1,w1=mi(op?invG:G,(P-1)/p);st<n;st+=p)
for(Re i=st,base=1;i<=st+len-1;++i){
Re tmp=(LL)f[i+len]*base%P;
f[i+len]=(f[i]-tmp+P)%P,(f[i]+=tmp)%=P,base=(LL)base*w1%P;
}
}
inline void times(Re *f,Re n,Re *g,Re m){
Re n_=n,m_=m;
for(m+=n,n=1;n<=m;n<<=1);invG=inv(G);
for(Re i=n_+1;i<n;++i)f[i]=0;
for(Re i=m_+1;i<n;++i)g[i]=0;
for(Re i=1;i<n;++i)tr[i]=(tr[i>>1]>>1)|((i&1)?n>>1:0);
NTT(f,n,0),NTT(g,n,0);
for(Re i=0;i<n;++i)f[i]=(LL)f[i]*g[i]%P;
NTT(f,n,1);Re invn=inv(n);
for(Re i=0;i<=m;++i)f[i]=(LL)f[i]*invn%P;
}
int c[N];
inline void polymi(Re *x,Re n,Re k,Re *s){
k%=P,s[0]=1;
for(Re i=1;i<=n;++i)s[i]=0;
while(k){
if(k&1){for(Re i=0;i<=n;++i)c[i]=x[i];times(s,n,c,n);}
for(Re i=0;i<=n;++i)c[i]=x[i];times(x,n,c,n),k>>=1;
}
}
int n,K,f[N],g[N];
int main(){
// freopen("123.txt","r",stdin);
in(n),--n,K=in_();
for(Re i=0;i<=n;++i)in(f[i]);
polymi(f,n,K,g);
for(Re i=0;i<=n;++i)printf("%d ",g[i]);
}
8.【多项式开方】
还不会,先咕着。
9.【多项式除法 / 取模】
还不会,先咕着。
10.【多项式对数函数 / 指数函数】
还不会,先咕着。
11.【多项式牛顿迭代】
还不会,先咕着。
12.【多项式多点求值 / 快速插值】
还不会,先咕着。
13.【多项式三角函数】
还不会,先咕着。
14.【多项式反三角函数】
还不会,先咕着。
15.【常系数齐次线性递推】
还不会,先咕着。
五:【博弈论】
1.【对抗搜索 (最大分数)】
【模板】一双木棋 \(\text{chess [}\) 九省联考 \(\text{2018] [P4363]}\)
(1).【记忆化】
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<map>
#define LL long long
#define Re register int
using namespace std;
const int N=13,inf=2e9;
int n,m,cnt,h[N],can[N],vis[N][N],A[2][N][N];
map<LL,int>pan;
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline LL Hash(Re op){LL ans=op+1;for(Re i=1;i<=n;++i)ans=ans*11ll+h[i];return ans;}
inline int dfs(Re op){
if(cnt==n*m)return 0;
LL H=Hash(op);
if(pan.find(H)!=pan.end())return pan[H];
Re ans=op?-inf:inf;
for(Re i=1,j;i<=n;++i)
if(h[i]<m&&vis[i][j=h[i]+1]==-1&&h[i-1]>=j){
vis[i][j]=op,++cnt,++h[i];
if(op)ans=max(ans,dfs(op^1)+A[op][i][j]);
else ans=min(ans,dfs(op^1)-A[op][i][j]);
vis[i][j]=-1,--cnt,--h[i];
}
return pan[H]=ans;
}
int main(){
// freopen("123.txt","r",stdin);
in(n),in(m);
for(Re i=1;i<=n;++i)
for(Re j=1;j<=m;++j)
in(A[1][i][j]);
for(Re i=1;i<=n;++i)
for(Re j=1;j<=m;++j)
in(A[0][i][j]);
memset(vis,-1,sizeof(vis));
h[0]=inf;
printf("%d\n",dfs(1));
}
(2).【Alpha-Beta 剪枝】
#include<algorithm>
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=13,inf=2e9;
int n,m,cnt,h[N],can[N],vis[N][N],A[2][N][N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int findmin(Re alpha,Re op);
inline int findmax(Re beta,Re op);
inline int findmin(Re alpha,Re op){
if(cnt==n*m)return 0;
Re ans=inf;
for(Re i=1,j;i<=n;++i)
if(h[i]<m&&vis[i][j=h[i]+1]==-1&&h[i-1]>=j){
vis[i][j]=op,++cnt,++h[i];
ans=min(ans,-A[op][i][j]+findmax(ans+A[op][i][j],op^1));
vis[i][j]=-1,--cnt,--h[i];
if(ans<=alpha)return ans;
}
return ans;
}
inline int findmax(Re beta,Re op){
if(cnt==n*m)return 0;
Re ans=-inf;
for(Re i=1,j;i<=n;++i)
if(h[i]<m&&vis[i][j=h[i]+1]==-1&&h[i-1]>=j){
vis[i][j]=op,++cnt,++h[i];
ans=max(ans,A[op][i][j]+findmin(ans-A[op][i][j],op^1));
vis[i][j]=-1,--cnt,--h[i];
if(ans>=beta)return ans;
}
return ans;
}
int main(){
// freopen("123.txt","r",stdin);
in(n),in(m);
for(Re i=1;i<=n;++i)
for(Re j=1;j<=m;++j)
in(A[1][i][j]);
for(Re i=1;i<=n;++i)
for(Re j=1;j<=m;++j)
in(A[0][i][j]);
memset(vis,-1,sizeof(vis));
h[0]=inf;
printf("%d\n",findmax(inf,1));
}
2.【对抗搜索 (胜负)】
\(\text{Find the Winning Move [UVA10111]}\)
(1).【Alpha-Beta 剪枝】
#include<algorithm>
#include<cstring>
#include<cstdio>
#define LL long long
#define Re register int
using namespace std;
const int N=6,inf=2e9;
int n=4,cnt,ansX,ansY,A[N][N];char op[5],s[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline int check(Re op){//检查op是否胜利
for(Re i=1;i<=n;++i){
Re cnt1=0,cnt2=0;//行、列
for(Re j=1;j<=n;++j)cnt1+=(A[i][j]==op),cnt2+=(A[j][i]==op);
if(cnt1==4||cnt2==4)return 1;
}
Re cnt1=0,cnt2=0;//对角线
for(Re i=1;i<=n;++i)cnt1+=(A[i][i]==op),cnt2+=(A[i][n-i+1]==op);
if(cnt1==4||cnt2==4)return 1;
return 0;
}
inline int findmin(Re alpha,Re op);//[op=0:对手的回合]
inline int findmax(Re beta,Re op);//[op=1:我的回合]
inline int findmin(Re alpha,Re op){//对手想让我尽量小(对手想让我输)
if(cnt==16)return 0;//和棋
if(check(op^1))return inf;//我达到最大分数(我连成了,我赢)
Re ans=inf;//准备一个最坏情况(对于对手来说)
for(Re i=1;i<=n;++i)
for(Re j=1;j<=n;++j)
if(A[i][j]==-1){
A[i][j]=op,++cnt;
ans=min(ans,findmax(ans,op^1));//在我的完美策略(让我尽量大)中取一个最小的
A[i][j]=-1,--cnt;
if(ans<=alpha)return ans;
//如果当前算出来的最小已经超过了下限alpha(超过了上一层的findmax中已算出的最大)
//那么继续做下去的话也一定不会对上一层的findmax产生贡献了
}
return ans;
}
inline int findmax(Re beta,Re op){//我想尽量大(我想让我赢)
if(cnt==16)return 0;//和棋
if(check(op^1))return -inf;//我达到最小分数(对手连成了,我输)
Re ans=-inf;//准备一个最坏情况(对于我来说)
for(Re i=1;i<=n;++i)
for(Re j=1;j<=n;++j)
if(A[i][j]==-1){
A[i][j]=op,++cnt;
ans=max(ans,findmin(ans,op^1));//在对手的完美策略(让我尽量小)中取一个最大的
A[i][j]=-1,--cnt;
ansX=i,ansY=j;//本题的特殊性:记录第一步选择的位置
if(ans>=beta)return ans;
//如果当前算出来的最大已经超过了上限beta(超过了上一层的findmin中已算出的最小)
//那么继续做下去的话也一定不会对上一层的findmin产生贡献了
}
return ans;
}
int main(){
// freopen("123.txt","r",stdin);
while(~scanf("%s",op)&&op[0]!='$'){
cnt=0;
for(Re i=1;i<=n;++i){
scanf("%s",s+1);
for(Re j=1;j<=n;++j)
if(s[j]=='.')A[i][j]=-1,++cnt;
else A[i][j]=(s[j]=='x');
}
if(cnt<=4)puts("#####");//当已有棋子不足4个时必定和局
else if(findmax(inf,1)==inf)printf("(%d,%d)\n",ansX-1,ansY-1);//我达到最大(我赢)
else puts("#####");//我达到最小(我输)
}
}

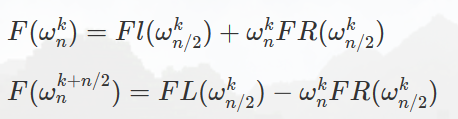
.PNG)


 浙公网安备 33010602011771号
浙公网安备 33010602011771号