CLUSTAL W论文解读
CLUSTAL W: improving the sensitivity of progressive multiple sequence alignment through sequence weighting, position-specific gap penalties and weight matrix choice.
通过序列加权、特定位置的间隙惩罚和权重矩阵的选择来提高渐进多序列比对的灵敏度。
Abstract
Firstly, individual weights are assigned to each sequence in a partial alignment in order to down- weight near-duplicate sequences and up-weight the most divergent ones.
首先,对部分比对中的每个序列分配单独的权重,以便对接近重复的序列进行降权重,而对最分散的序列进行升权重。
Secondly, amino acid substitution matrices are varied at different alignment stages according to the divergence of the sequences to be aligned.
其次,氨基酸替代矩阵在不同的比对阶段根据待比对序列的不同而不同。
Thirdly, residue-specific gap penalties and locally reduced gap penalties in hydrophilic regions encourage new gaps in potential loop regions rather than regular secondary structure.
第三,残基特异性缺口惩罚和亲水性区域局部减少的缺口惩罚鼓励潜在环区出现新的缺口,而不是规则的二级结构。
Fourthly, positions in early alignments where gaps have been opened receive locally reduced gap penalties to encourage the opening up of new gaps at these positions.
第四,在早期调整中,已有缺口的职位将在当地减少缺口处罚,以鼓励在这些职位上开辟新的缺口。
Introduction
Currently, the most widely used approach is to exploit the fact that homologous sequences are evolutionarily related. One can build up a multiple alignment progressively by a series of pairwise alignments, following the branching order in a phylogenetic tree. One first aligns the most closely related sequences, gradually adding in the more distant ones. This approach is sufficiently fast to allow alignments of virtually any size.
目前,最广泛使用的方法是利用同源序列在进化上是相关的这一事实。人们可以按照系统发育树中的分支顺序,通过一系列成对的比对逐步建立多重比对。首先比对关系最密切的序列,然后逐渐添加距离较远的序列。这种方法足够快,几乎可以进行任何大小的对齐。
There are two major problems with the progressive approach: the local minimum problem and the choice of alignment parameters.
渐进法有两个主要问题:局部极小值问题和对齐参数的选择。
The local minimum problem
The local minimum problem stems from the 'greedy' nature of the alignment strategy. The algorithm greedily adds sequences together, following the initial tree. There is no guarantee that the global optimal solution, as defined by some overall measure of multiple alignment quality, or anything close to it, will be found. More specifically, any mistakes (misaligned regions) made early in the alignment process cannot be corrected later as new information from other sequences is added.
局部最小问题源于对齐策略的“贪婪”性质。该算法按照初始树的顺序贪婪地将序列相加在一起。不能保证找到全局最优解,该全局最优解由多个比对质量的某个总体度量或任何接近它的度量来定义。更具体地说,当来自其他序列的新信息被添加时,在比对过程早期所犯的任何错误(未对齐区域)都不能在以后纠正。
The only way to correct this is to use an iterative or stochastic sampling procedure.
解决这个问题的唯一方法就说使用迭代法或者随机抽样(不知道是啥)
The alignment parameter choice problem
The alignment parameter choice problem is, in our view, at least as serious as the local minimum problem.
Stochastic or iterative algorithms will be just as badly affected as progressive ones if the parameters are inappropriate: they will arrive at a false global minimum.
Traditionally, one chooses one weight matrix and two gap penalties (one for opening a new gap and one for extending an existing gap) and hope that these will work well over all parts of all the sequences in the data set. When the sequences are all closely related, this works.
传统上,人们选择一个权重矩阵和两个缺口惩罚(一个用于打开新的缺口,另一个用于扩大现有的缺口),并希望这些惩罚将在数据集中所有序列的所有部分都能很好地工作。当所有序列都紧密相关时,这是可行的。
The first reason is that virtually all residue weight matrices give most weight to identities. When identities dominate an alignment, almost any weight matrix will find approximately the correct solution. With very divergent sequences, however, the scores given to non-identical residues will become critically important; there will be more mismatches than identities. Different weight matrices will be optimal at different evolutionary distances or for different classes of proteins.
第一个原因是几乎所有的残留权重矩阵都赋予恒等式最大的权重。当恒等式在排列中占主导地位时,几乎任何权重矩阵都会找到近似正确的解。然而,对于非常不同的序列,给予不同残基的分数将变得至关重要;错配将比同一性更多。不同的权重矩阵在不同的进化距离或不同类别的蛋白质中是最优的。
The second reason is that the range of gap penalty values that will find the correct or best possible solution can be very broad for highly similar sequences (11). As more and more divergent sequences are used, however, the exact values of the gap penalties become important for success. In each case, there may be a very narrow range of values which will deliver the best alignment.
第二个原因是,对于高度相似的序列(11),将找到正确或最佳可能解决方案的差距罚值的范围可能非常宽。然而,随着越来越多的不同序列被使用,差距惩罚的精确值对于成功变得重要。在每种情况下,提供最佳对齐的值范围都可能非常窄。
Neighbour-Joining NJ
In the original CLUSTAL programs, the initial guide trees, used to guide the multiple alignment, were calculated using the UPGMA method (20). We now use the Neighbour-Joining method which is more robust against the effects of unequal evolutionary rates in different lineages and which gives better estimates of individual branch lengths. This is useful because it is these branch lengths which are used to derive the sequence weights.
将UPGMA层次聚类换成了NJ层次聚类。
Material and Methods
The basic alignment method
The basic multiple alignment algorithm consists of three main stages: (i) all pairs of sequences are aligned separately in order to calculate a distance matrix giving the divergence of each pair of sequences; (ii) a guide tree is calculated from the distance matrix; (iii) the sequences are progressively aligned according to the branching order in the guide tree.
- 比对所有序列对,计算得出距离矩阵
- 根据距离矩阵计算指导树
- 根据指导树的顺序逐步对序列进行比对
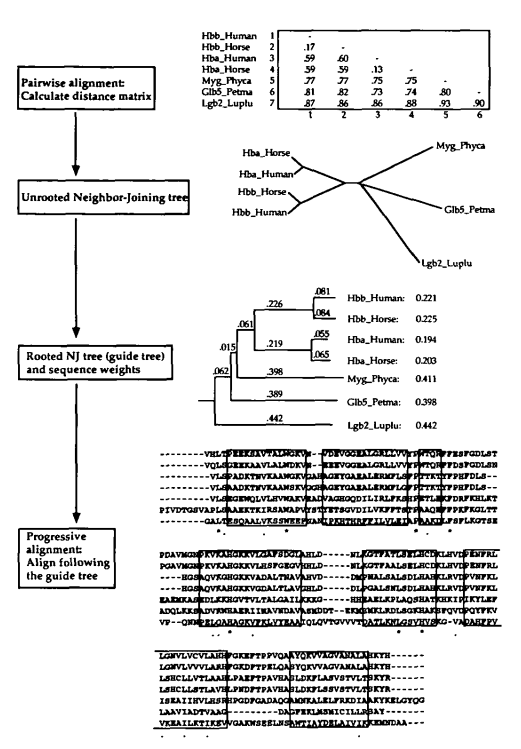
Calculate distance matrix
In the original CLUSTAL programs, the pairwise distances were calculated using a fast approximate method.
This allows very large numbers of sequence to be aligned, even on a microcomputer. The scores are calculated as the number of k-tuple matches (runs of identical residues, typically 1 or 2 long for proteins or 2 - 4 long for nucleotide sequences) in the best alignment between two sequences minus a fixed penalty for every gap.
分数的计算方法是两个序列之间的最佳比对中的k-字节组匹配的数量(相同残基,对于蛋白质通常为1或2,对于核苷酸序列通常为2-4) 减去每个gap的固定惩罚。
We now offer a choice between this method and the slower but more accurate scores from full dynamic programming alignments using two gap penalties (for opening or extending gaps) and a full amino acid weight matrix.
These scores are calculated as the number of identities in the best alignment divided by the number of residues compared (gap positions are excluded). Both of these scores are initially calculated as per cent identity scores and are converted to distances by dividing by 100 and subtracting from 1.0 to give number of differences per site.
Progressive alignment
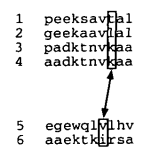
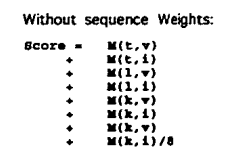
组与组的比对,每个位置都需要计算得分。