与数组初始状态无关的内排序算法

首先，与初始状态无关分为几种情况

1、算法复杂度与初始状态无关；

2、元素总比较次数与初始状态无关；

3、元素总移动次数与初始状态无关。

【其实还有一种就是总排序趟数与初始状态无关，由于分析简单，除了快速排序的排序次数（递归深度）与关键字选择（初始状态）有关，还有一个优化后的冒泡排序和后序是否有序有关，其他均只与总长度n有关，与初始状态无关，故不做分析】

 

 

首先看内排序总结表：

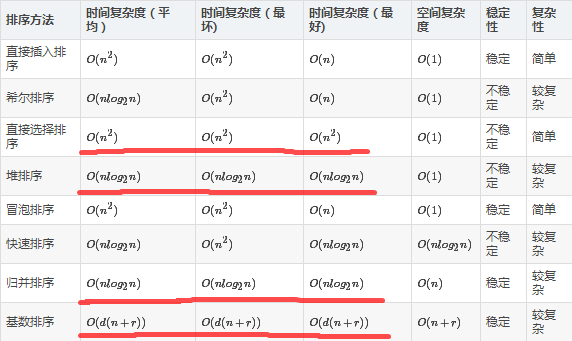
 由表中红线标出的地方可以轻易得出以下四种排序方法的算法复杂度与数组的初试状态无关：

一堆（堆排序）乌龟（归并排序）选（选择排序）基（基数排序）友（摘自牛友 sunlight_run）

我是这么记的：两个选择排序和两个复杂排序（选择、插入、交换我列为简单排序）。

 

稍加判断得到，以上三种情况2、3是必定包含在情况1中间的。

所以接下来分别列举这四个个算法讨论比较次数以及移动次数（以升序排序为例，不赘述代码）。

【最近很忙，没时间画图，用文字总结的，嘿嘿，就将就看吧，等今年冬天有时间了再添几个图~~】

• 堆排序

　　　　思想：首先对初始数组建立最小堆，然后取堆顶元素与堆尾交换，再此堆元素（不含堆尾）再重新构建最小堆，依次循环。

　　　　分析：由于建立最小堆其实就是将初始元素按照规定的准则进行一系列排序（包括层级向下比较、交换），所以如果元素一开始就已经是最小堆则不需要此时的交换且大大减少向下比较次数，

　　　　　　所以堆排序不属于情况二也不属于情况三。

• 归并排序

　　　　思想：将初试数组划分成N个子数组，两两进行合并排序，然后结果再和其他同级合并后的数组合并知道合并完所有。

　　　　分析：外层递归与初始无关，主要思考合并排序中的比较和交换即可。合并排序思想：将数组A第一个与数组B第一个比较，较小的那一个直接进入result数组并且指针向下移动再与对面数组第一个比较，依次类推，然后将还有剩余的数组内元素全放入result，最后用result将原数组中对应的值一一替换。因此，假设初始数组就是有序的，那么每次合并排序的时的比较次数都仅仅是一个待合并的数组的长度，因此比较次数与初始状态有关，归并排序不属于情况二。　　　　　　

　　　　　　然而，不论一开始的状态如何，最后都是两个数组进入result，移动次数都为两个待合并数组的长度和，然后再将result内元素全部移动到原来数组进行替换。所以元素移动次数与初始状态无关，归并排序属于情况三。

• 选择排序　　

　　　　思想：i 从头开始，每次遍历之后所有的元素，k 从 i 开始，向后标记最小的元素，循环后如果大于 i ，则与 i 位置元素交换，一直到最后。

　　　　分析：比较次数都是N-1的阶乘，与初始状态无关，所以选择排序属于情况二。

　　　　　　　交换次数当全部已经排序好时则不发生交换，所以选择排序不属于情况三。

• 基数排序

　　　　思想：将数组从低位到高位，每到一位对应分入10个桶（0-9）中，依次到最高位，由于每上升一位，处于“0号桶”中的数据都会将此位之前的数字排好，以此达到排序效果。

　　　　分析：基数排序中并不发生任何元素之间的比较，所以基数排序属于情况二。

　　　　　　　不论初始数组如何排列，都是从个位开始，各自进入自己个位对应的位置，之后也都是一样，所以元素移动次数一样，所以基数排序属于情况三。

 

综上所述：

　　

1、算法复杂度与初始状态无关的有：选择排序、堆排序、归并排序、基数排序。

2、元素总比较次数与初始状态无关的有：选择排序、基数排序。

3、元素总移动次数与初始状态无关的有：归并排序、基数排序。

 

欢迎讨论。