最短Hamilton路径
题目描述
给定一张 n 个点的带权无向图,点从 0~n-1 标号,求起点 0 到终点 n-1 的最短Hamilton路径。 Hamilton路径的定义是从 0 到 n-1 不重不漏地经过每个点恰好一次。
输入格式
第一行输入整数 n。
接下来 n 行每行 n 个整数,其中第 i 行第 j 个整数表示点 i 到 j 的距离(记为 a[i,j])。
对于任意的 x,y,z,数据保证 a[x,x]=0,a[x,y]=a[y,x] 并且 a[x,y]+a[y,z]≥a[x,z]。
输出格式
输出一个整数,表示最短 Hamilton 路径的长度。
数据范围
1≤n≤20
0≤a[i,j]≤107
输入样例:
5
0 2 4 5 1
2 0 6 5 3
4 6 0 8 3
5 5 8 0 5
1 3 3 5 0
输出样例:
18
思路
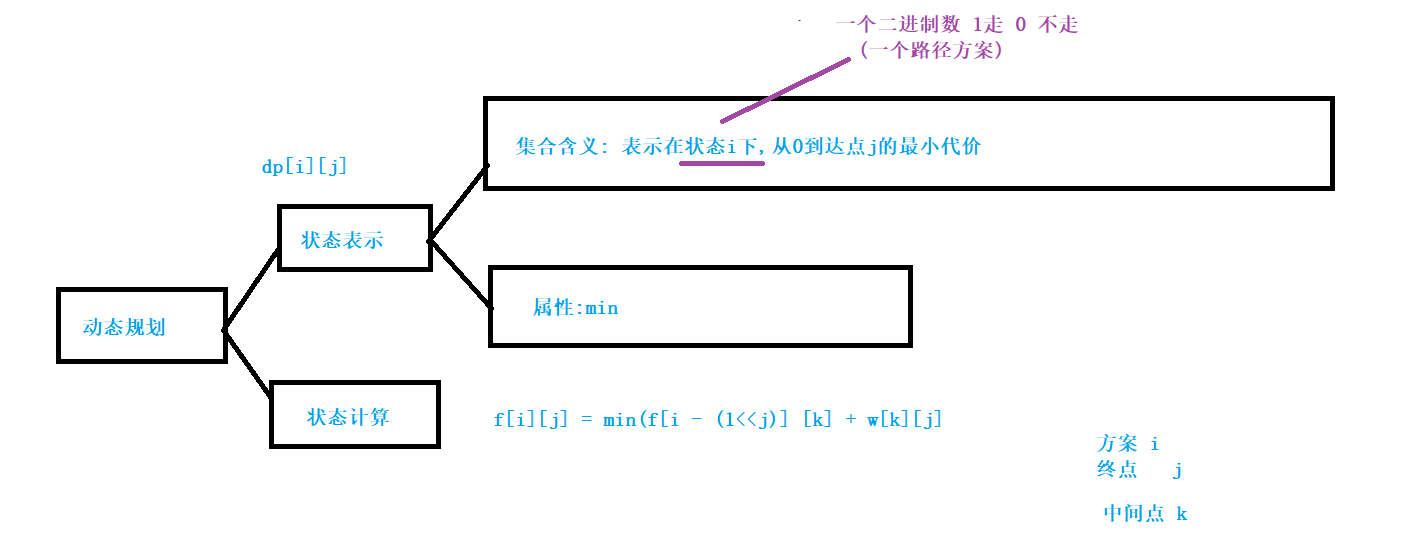
这道旅行商NP完全问题,如果暴力的话 所有方案数是 n! 对每种方案走一遍Hamilton取一个min那就是 n! * n的时间复杂度,20!是个很大的数字,肯定要优美的去枚举,降低复杂度;
如何去降低那?我们用二进制去枚举,将所有状态压缩成一个二进制数,然后用状态压缩dp去求
由于每个点只能恰好经过一次,那么我在i方案下最优解的j ,也是由中间点到达k的最优解 f[i-(1<<j)][k],(在i方案下去掉 j在这一位下的影响,就是实际 k的方案,也就是 i-(1<<j)😉 在加上代价w[k][j];符合最优子结构
//这里填你的代码^^
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 20;
int dp[1<<20][N];
int w[N][N];
int main()
{
int n;
cin >> n;
for (int i = 0; i < n ; i ++)
{
for (int j = 0; j < n; j ++)
{
cin >> w[i][j];
}
}
memset(dp,0x3f,sizeof(dp)); //初始化为最大
dp[1][0] = 0;
for(int i = 1; i <= (1<<n); i ++) //枚举所有状态
{
if(i & 1) //起点必须走
{
for(int j = 0; j < n; j ++) //枚举终点
{
if(i>>j & 1) //如果在二进制中是1 , 说明要走
{
for(int k = 0; k < n; k ++) //从k到达j的点
{
if(i-(1<<j) >>k & 1) //如果把j状态去掉, k这一位仍是1 状态转移
{
dp[i][j] = min (dp[i][j],dp[i-(1<<j)][k]+w[k][j]);
}
}
}
}
}
}
cout<<dp[(1<<n)-1][n-1]; //1<<n -1 表示的含义就是 0到n-1的点在二进制下全是1 ,也就是符合Hamilton
return 0;
}
//注意代码要放在两组三个点之间,才可以正确显示代码高亮哦~

