The xor-longest Path POJ - 3764 字典树+树的遍历

The xor-longest Path
Time Limit: 2000MS Memory Limit: 65536K

Description

In an edge-weighted tree, the xor-length of a path p is defined as the xor sum of the weights of edges on p:

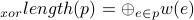
⊕ is the xor operator.
We say a path the xor-longest path if it has the largest xor-length. Given an edge-weighted tree with n nodes, can you find the xor-longest path? 　

Input

The input contains several test cases. The first line of each test case contains an integer n(1<=n<=100000), The following n-1 lines each contains three integers u(0 <= u < n),v(0 <= v < n),w(0 <= w < 2^31), which means there is an edge between node u and v of length w.

Output

For each test case output the xor-length of the xor-longest path.
Sample Input

4
0 1 3
1 2 4
1 3 6
Sample Output

7
Hint

The xor-longest path is 0->1->2, which has length 7 (=3 ⊕ 4)

题意

给你一棵树,共有n-1条边,让你去找一条最大的异或路径,说白了,就是假设树上由x个点,a,b是任意两个点,设 1<=a<=b<=x, 由于是树,a,b两个点之间一定连通,求 a,b两点之间路径的连续异或和;

思路

想一下,暴力做法,枚举所有的起点,在遍历起点的所有路径,然后记录最大的异或值,时间复杂度O(n^n),会TLE的;
在从头开始想,任意设一个起点作为我们这棵树的根,就设成0这个点吧,
定义f[i]为我定义的根节点(0)到其他点的异或和
则任意两点a,b的异或路径和 为 f[0,a]^f[0,b]
那DFS,就可以这样写,dfs 要传的参数有什么?,
1.当前遍历的起点 u
2.遍历结束的标记点 father
3.该条路径的异或值 (记得存到F[ ]数组里面)
DFS后,开始字典树,把所有F[i] 插入 字典树中,然后query找最大异或就🆗了

这题记得多组输入,内存大小一定要开对,否则就会在RE 和 ME 中边缘拉扯;

代码

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
typedef long long ll;
using namespace std;
const int maxn=112222;
const int maxn1=3122222;
int n,tol,head[maxn];
int son[maxn1][2];
int idx;
ll f[maxn];
void IOS(){
   ios::sync_with_stdio(false);
   cin.tie(0);
   cout.tie(0);
}
struct node{
	int to;
	ll cost;
	int next;
}edge[maxn*2]; 
void add(int u,int v,ll w)
{
	edge[tol].to=v;
	edge[tol].cost=w;
	edge[tol].next=head[u];
	head[u]=tol++;
}
void insert(ll x)
{
	int p=0;
	for(int i=31;i>=0;i--)
	{
		int u=x>>i&1;
		if(!son[p][u])
		son[p][u]=++idx;
		p=son[p][u];
	}
}
ll query(ll x)
{
	ll res=0;
	int p=0;
	for(int i=31;i>=0;i--)
	{
		int u=x>>i&1;
		if(son[p][!u])
		{p=son[p][!u];
		res=res*2+1;}
		else
		{
			p=son[p][u];
			res=res*2+0; 
		}
		
	}
	return res;
}
void dfs(int u,int father,ll sum)
{
	f[u]=sum;
	for(int i=head[u];i!=-1;i=edge[i].next)
	{
		
		int v=edge[i].to;
		if(v!=father)
		{
			dfs(v,u,sum ^ edge[i].cost);
		}
	}
}
int main()
{  
   while(~scanf("%d",&n))
  {
   
	memset(head,-1,sizeof(head));
	memset(son,0,sizeof(son));
	memset(f,0,sizeof(f));
	idx=0;
	tol=0;
	for(int i=0;i<n-1;i++)
	{
		int u,v,w;
	    scanf("%d%d%d",&u,&v,&w);
		add(u,v,w);
		add(v,u,w);
	}
	dfs(0,-1,0);
	ll ans=0;
	for(int i=0;i<n;i++)
	{
		insert(f[i]);
	}
	for(int i=0;i<n;i++)
	{
		ans=max(ans,query(f[i]));
	}
	printf("%lld\n",ans) ;
}  
}