HDU Kanade Loves Maze Designing 树的遍历

Problem Description

Sample Input

1
6
1 1 2 2 3
1 1 4 5 1 4

Sample Output

495644981 518101442
495644981 518101442
397599492 896634980
612255048 326063507
495644981 518101442
397599492 896634980

Hint

Let A=(aij), then for the example, A equals to
1 1 2 2 1 2
1 1 2 2 1 2
2 2 1 3 2 1
2 2 3 1 2 3
1 1 2 2 1 2
2 2 1 3 2 1

题目大意:

给你一棵 n 个节点的树,一共有 n-1 条边,每个节点都有一个种类,
定义a[i,j] 为 在 i->j 这条路径上,共有几种不同种类的节点

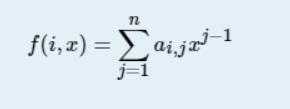
题目思路

这个公式中 x^ j-1 ,可以用 快速幂去求 , 主要难点在于求 a[i,j]
显然需要利用树的DFS去遍历每个起点,然后在 dfs中 将答案记录 ,记得 需要回溯

 void dfs(当前遍历节点 x , 父节点 fa  , 此次dfs遍历的起点 root)
{
        cnt[c[x]]++;
	if(fa==0) f[root][x] = 1; 
	else
	{
		if(cnt[c[x]] == 1) f[root][x] = f[root][fa]+1; 
		else f[root][x]=f[root][fa];
	}
	
	for(int i = head[x] ; i != -1 ; i = edge[i].next)
	{   int y = edge[i].to;
	   if( y == fa) continue;
		dfs(y , x , root);
		cnt[c[y]]--;
	}
}

代码

#include <iostream>
#include <algorithm>
#include <cstring>
#include <map>
using namespace std;
typedef long long ll;
const int maxn=2e4+5;
int n,tol,head[maxn],vis[maxn];
int p[maxn],c[maxn];
int f[2005][2005];
int cnt[20005];
struct node{
    int to,next;
}edge[maxn];
void add_edge(int u,int v)
{
    edge[tol].to=v;   
    edge[tol].next=head[u];
    head[u]=tol++;
}
const int mod1=1e9+9;
const int mod2=1e9+7;
int ans = 0;
ll p1[maxn];
ll p2[maxn];
void dfs(int x , int fa , int root)
{
	cnt[c[x]]++;
	if(fa==0) f[root][x] = 1;
	else
	{
		if(cnt[c[x]] == 1) f[root][x] = f[root][fa]+1;
		else f[root][x]=f[root][fa];
	}
	
	for(int i = head[x] ; i != -1 ; i = edge[i].next)
	{   int y = edge[i].to;
	   if( y == fa) continue;
		dfs(y , x , root);
		cnt[c[y]]--;
	}
	
}
ll ksm(ll base, ll power,int mod) 
{
    ll result = 1;
    while (power > 0) 
    {
        if (power & 1) 
        {
            result = result * base %mod;
        }
        power >>= 1;
        base = (base * base) %mod;
    }
    return result;
}

int main()
{
    int T;
   scanf("%d",&T);
    while (T --)
    {
       
        scanf("%d",&n);
        tol = 0;
        memset(head,-1,sizeof(head));
        for(int i = 2; i <= n ; i++)
        {
                scanf("%d",&p[i]);
            add_edge(i,p[i]);
            add_edge(p[i],i);
        }
        for(int i = 1; i <= n ; i++)
        {
            scanf("%d",&c[i]);
        }
        for(int i = 1; i <= n ; i++)
        {  memset(cnt,0,sizeof(cnt));
        	dfs(i,0,i);
		}
        ll res=0;
        ll res1=0;
        for(int i = 0; i <= n ; i++)
        {
        	p1[i] = ksm(19560929,i,mod2);
        	p2[i] = ksm(19560929,i,mod1);
		}
        for(int i=1;i<=n;i++){
        	
            res=0,res1=0;
            
            for(int j=1;j<=n;j++){
                res+=(f[i][j]*p1[j-1])%mod2;
                res1+=(f[i][j]*p2[j-1])%mod1;
            }
            printf("%lld %lld\n",res%mod2,res1%mod1);
        
    }
}
}