深度优先搜索 DFS 学习笔记
深度优先搜索 学习笔记
引入
深度优先搜索 DFS 是图论中最基础,最重要的算法之一。DFS 是一种盲目搜寻法,也就是在每个点 上,任选一条边 DFS,直到回溯到 时才选择别的边,如下图。
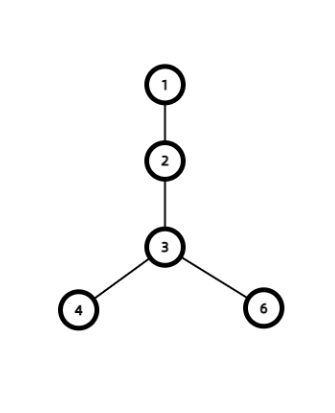
他的搜索顺序为 1-2-3-4-6。
递归实现指数型枚举
从 中这 个整数选取任意多个,输出所有可能的选择方案。
每一个数都有选与不选两种可能,相当于在每次递归上尝试选与不选两种分支,最后的时间复杂度即为 。
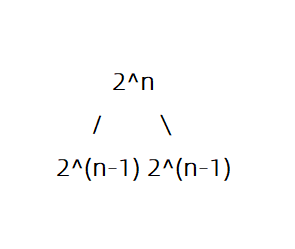
递归实现组合型枚举
组合型枚举的实现与指数型枚举的实现十分相近,只不过该问题是必须要在 个数中选取 个数,每个数还是有选、不选两条分支,所以实现直接在“指数型枚举”中加入两个剪枝即可:
- 若当前选择的数的个数大于 直接返回。
- 若当前选择的数的个数加上剩余的数的个数小于 则直接返回。
时间复杂度 。
递归实现排列型枚举
题目链接:题目详情 - 全排列问题 - ClorOJ (zshfoj.com)。
把每个可用的数作为数列中的下一个数,求解把剩余的 个数按照任意次序排列这个规模更小的子问题。
时间复杂度 。
例题1 拔河比赛
题目链接:题目详情 - 拔河比赛 - ClorOJ (zshfoj.com)。
首先,由 (1) 可得,若 为奇数,则两边的人数仅相差 ,否则若 为偶数,则两边人数相等。
考虑到条件 (1),显然我们可以只构造一个长度为 的组。
再考虑到条件 (2),显然两个组的体重之和 是固定的,肯定为 。于是我们需要让这个长度为 的组的和尽量接近 。
于是我们可以遍历每一个人,每个人要么选要么不选,即“指数型枚举”,在所有方法中找出最小的差值,即为答案。用一个三元组 来描述状态,表示当前考虑到第 位成员,已经选择了 个人,体重和为 。
代码:
#include<cstdio>
#include<cstring>
#include<cmath>
using namespace std;
int t,n,a[100100],b[100100],s=999999999,p;
inline int min(int x,int y){return x>y?y:x;}
inline void dfs(int k,int x,int u)
{
if(x>(n-x+1)) return;
if(abs(x-n+x)<2) s=min(s,abs(k));
for(int i=u+1;i<=n;i++)
{
if(b[i]<1)
{
b[i]=1;
dfs(k-2*a[i],x+1,i);
b[i]=0;
}
}
}
int main()
{
scanf("%d",&t);
while(t--)
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&a[i]);
p+=a[i];
}
dfs(p,0,0);
printf("%d\n",s);
for(int i=1;i<=n;i++) b[i]=0;
p=0;
s=999999999;
}
return 0;
}
剪枝
每次搜索可以看做从树根出发,遍历整棵树的过程。而所谓剪枝,即为通过某种判断,将不必要的遍历过程剪去。
使用剪枝优化的核心问题是设计剪枝的判断方法,即确定哪些枝条应该舍去,哪些枝条应该保留。设计出好的剪枝判断方法往往能使得程序运行时间大幅度缩短,否则,也可能适得其反,因为判断也需要时间。
剪枝的原则
正确性
顾名思义,剪枝需要保证正确性,否则可能会遗漏掉更优的枝条。如果剪去了正确的答案,那么剩下的操作都毫无意义。所以正确性是剪枝的前提。
准确性
尽可能剪去多的不能通向正解的枝条。剪枝方法只有在具有了较高准确性的时候,才能真正的优化时间。
高效性
当设计好剪枝后,我们可能需要对搜索树的每个枝条都进行一次判断。然而,我们一般的剪枝是基于正解的“必要条件”进行判断,所以必然有很多非正解的枝条没有被剪枝。这些情况下的剪枝判断操作,对于程序效率的提高无疑是具有副作用的。所以如何平衡剪枝算法的准确性与高效性,往往是搜索算法优化的关键。
剪枝的技巧
优化搜索顺序
搜索数的各个层次,各个分支之间的顺序不是固定的,不同的搜索顺序会产生不同的搜索树。
排除等效冗余
如果沿着几条不同的分支能达到的子树是等效的,那么我们只需要对其中的一条分支进行搜索即可。
可行性剪枝
对当前状态进行检查,发现若分支无法到达正确答案的递归边界,则执行回溯。好比你在路上走,远远看到前方是死胡同,则直接折返绕路。在某些题目中也称“上下界剪枝”。
最优性剪枝
在最优化问题中,若当前花费的代价已经高于之前搜到的最优解,则直接返回,因为无法比之前搜到的最优解更优了。
记忆化
记录每个状态的搜索结果,在重复遍历一个状态时直接返回之前搜过的答案。此方法应用在 DFS 搜索为图的时候,如斐波那契数列。
例题2 数独游戏
Description
把 的数独补充完整,使得图中每行、每列、每个 的九宫格内数字 均恰好出现一次。
考虑 DFS。
Solution 1
找出一个还没有填的位置,检查 所有合法的数字。
搜索边界:1. 填满 的数独;2. 发现一个位置没有能填的合法数字。
可是这样的时间复杂度还是很大。
Solution 2
考虑优化搜索顺序,我们应该优先考虑“能填的合法数字”最少的位置。考虑这个位置上填什么数字。
此外,在每个状态上记录,检索,更新的开销。用位运算代替对数独各个位置所填的数字的记录,以及可填性的检查与统计。
- 对于每行、每列、每个九宫格,分别用一个 9 位二进制数保存哪些数字可以填。
- 若一行为
101100010,即 为不可以填写的,而 是可以填写的。 - 这里的位运算是可以自行选择的。
- 若一行为
- 可以做或运算,来判断某个数是否可以用。
- 当填写后,我们需要把九宫格更新。
Code
#include <iostream>
#include <cmath>
#include <cstring>
using namespace std;
int a[100][100], b[100][2], c[100], fx[10][10], fy[10][10], fg[10][10], n;
string s;
bool check(int x, int y, int t) //判断是否可填该数
{
if (fx[x][t] || fy[y][t] || fg[(x - 1) / 3 * 3 + (y - 1) / 3 + 1][t])
return false;
else //无重复,即可填,判重数组标记为一
{
fx[x][t] = 1;
fy[y][t] = 1;
fg[(x - 1) / 3 * 3 + (y - 1) / 3 + 1][t] = 1;
return true;
}
}
void back(int x, int y, int t) //回溯,还原信息
{
fx[x][t] = 0;
fy[y][t] = 0;
fg[(x - 1) / 3 * 3 + (y - 1) / 3 + 1][t] = 0;
}
bool dfs(int dep) {
if (dep > n) {
n = 0;
for (int i = 1; i <= 9; i++) {
for (int j = 1; j <= 9; j++) {
if (a[i][j])
cout << a[i][j];
else
cout << c[++n];
}
}
cout << endl;
return true; //返回真,以便快速退出
} else {
int x = b[dep][0], y = b[dep][1];
for (int i = 1; i <= 9; i++) {
if (check(x, y, i)) {
c[dep] = i; //另存空格填的数
if (dfs(dep + 1))
return true; //直接退出
back(x, y, i);
}
}
}
return false;
}
int main() {
getline(cin, s);
while (s != "end") {
for (int i = 0; i < 81; i++) {
int xt = i / 9, yt = i % 9;
if (s[i] == '.') {
a[xt + 1][yt + 1] = 0;
b[++n][0] = xt + 1, b[n][1] = yt + 1; //存下空格坐标
} else {
a[xt + 1][yt + 1] = s[i] - 48;
fx[xt + 1][s[i] - 48] = 1;
fy[yt + 1][s[i] - 48] = 1;
fg[(xt / 3 * 3 + yt / 3 + 1)][s[i] - 48] = 1;
}
}
dfs(1);
n = 0;
memset(fx, 0, sizeof(fx));
memset(fy, 0, sizeof(fy));
memset(fg, 0, sizeof(fg));
getline(cin, s);
}
}
例题3 虫食算
Description
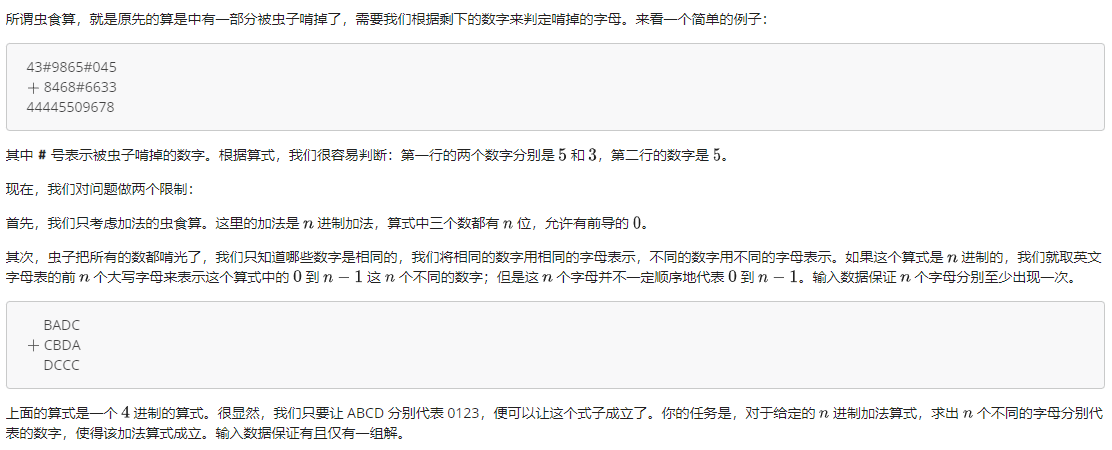
.
Solution
考虑 DFS。很明显可以依次枚举每个字母代表什么数字,但 的复杂度很明显无法通过本题 的数据。
如何剪枝?做加法竖式的时候要从右到左计算,考虑如何判断当前方案不合法。
- 从后往前枚举每一列,记当前的被加数、加数与和分别为 ,进位为 ,若出现 的情况则不合法。
- 若右边存在某个数尚未确定,那么上一位的 可能为 中的任意一个。这是若 且 ,那么也是不合法。
- 对于最高位判断是否有进位,若有进位则根据题意,和也是一个 位数,不合法。
Code
#include <bits/stdc++.h>
#define N 55
using namespace std;
int n, ct;
int a[N], b[N];
char s[4][N];
void dfs(int x, int y, int t) {
if (ct == 1)
return;
if (y == -1) {
if (t == 0) {
for (int i = 0; i < n; ++i) printf("%d ", a[i]);
ct = 1;
}
return;
}
for (int i = y; i >= 0; --i) {
int a1 = a[s[1][i] - 'A'], a2 = a[s[2][i] - 'A'], a3 = a[s[3][i] - 'A'];
if (a1 == -1 || a2 == -1 || a3 == -1)
continue;
if ((a1 + a2) % n != a3 && (a1 + a2 + 1) % n != a3)
return;
}
if (a[s[x][y] - 'A'] < 0) {
for (int i = n - 1; i >= 0; --i) {
if (b[i] == 0) {
if (x != 3) {
a[s[x][y] - 'A'] = i;
b[i] = 1;
dfs(x + 1, y, t);
a[s[x][y] - 'A'] = -1;
b[i] = 0;
} else {
int sum = a[s[1][y] - 'A'] + a[s[2][y] - 'A'] + t;
if (sum % n != i)
continue;
b[i] = 1;
a[s[x][y] - 'A'] = i;
dfs(1, y - 1, sum / n);
b[i] = 0;
a[s[x][y] - 'A'] = -1;
}
}
}
return;
}
if (x != 3) {
dfs(x + 1, y, t);
} else {
int sum = a[s[1][y] - 'A'] + a[s[2][y] - 'A'] + t;
if (sum % n != a[s[3][y] - 'A'])
return;
dfs(1, y - 1, sum / n);
}
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= 3; ++i) scanf("%s", s[i]);
memset(a, -1, sizeof(a));
dfs(1, n - 1, 0);
return 0;
}
总结
- 深搜其实还是非常好用的。
- 骗分。
- 其实深搜的功能远远不止骗分,请举一反三。



【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 微软正式发布.NET 10 Preview 1:开启下一代开发框架新篇章
· 没有源码,如何修改代码逻辑?
· NetPad:一个.NET开源、跨平台的C#编辑器
· PowerShell开发游戏 · 打蜜蜂
· 凌晨三点救火实录:Java内存泄漏的七个神坑,你至少踩过三个!