线性DP（上）
线性DP
1.线性DP简介
线性DP这类动态规划问题的状态一般是一维的f[i]，第i个元素的
最优值只与前i-1个元素的最优值（正推）或第i+1个元素
之后的最优值（倒推）有关。
2.经典例题（1）：数字金字塔
观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。
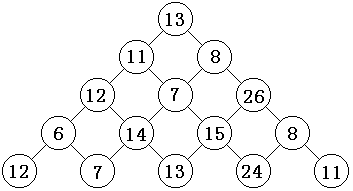
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。
输入格式
第一个行包含\(R\)，表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
输出
单独的一行，包含那个可能得到的最大的和。
输入样例
5
13
11 8
12 7 26
6 14 15 8
12 7 13 24 11
输出样例
86
数据范围
\(1≤R≤1000\)
\(0\leq\) 金字塔中的整数 \(\leq 100\)
注：本题来源于信息学奥赛一本通第1258题
3.经典例题（1）思路
通过观察题目可以得到：
当前位置的最大值可以通过来自左上和来自右上的最大值的最大值加自身来求得。
所以状态转移方程为：
4.经典例题（1）代码
代码不难理解，但细节较多，请仔细分辨。
#include<iostream>
using namespace std;
const int N=1005,INF=0x3f3f3f3f;
int n,ans=-INF;
int a[N][N],f[N][N];//三角形和DP数组
int main(){
cin>>n;
for(int i=1;i<=n;i++)
for(int j=1;j<=i;j++)
cin>>a[i][j];
for(int i=0;i<=n;i++)
for(int j=0;j<=i+1;j++)
f[i][j]=-INF;//初始化，边缘需要特判
f[1][1]=a[1][1];
for(int i=2;i<=n;i++)//注意，从2开始，因为i=1时前一行已经算过
for(int j=1;j<=i;j++)
f[i][j]=max(f[i-1][j-1]+a[i][j],f[i-1][j]+a[i][j]);
for(int i=1;i<=n;i++) ans=f[n][i]>ans?f[n][i]:ans;//算最大值
cout<<ans;
return 0;
}
5.经典例题（2）：最长上升子序列
题目描述
一个数的序列 \(b_i\)，当 \(b_1<b_2<...<b_S\) 的时候，我们称这个序列是上升的。
对于给定的一个序列 \((a_1,a_2,...,a_N)\)，我们可以得到一些上升的子序列 \((a_i1,a_i2,...,a_iK)\)，这里 \(1≤i_1<i_2<...<i_K\leq N\)。
比如，对于序列 \((1,7,3,5,9,4,8)\),有它的一些上升子序列，如 \((1,7)\),\((3,4,8)\)等等。这些子序列中最长的长度是 \(4\)，比如子序列\((1,3,5,8)\)。
你的任务，就是对于给定的序列，求出最长上升子序列的长度。
输入
输入的第一行是序列的长度 \(N\)，第二行给出序列中的 \(N\) 个整数。
输出
最长上升子序列的长度。
输入样例
7
1 7 3 5 9 4 8
输出样例
4
数据范围
\(1≤N≤1000\)
\(0 \leq\) 序列中的数字 \(\leq 10000\)
注：本题来源于信息学奥赛一本通第1281题
6.经典问题（2）思路
其实特别简单，
我们这次可以用 \(f\) 数组来代表截止到 \(i\) 的上升子序列的最大长度，
在设个 \(ans\) 来统计答案。
就完了……
直接上代码！
7.经典问题（2）代码
#include<iostream>
using namespace std;
const int N=1005;
int n,res;
int a[N],f[N];
int main(){
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++){
f[i]=1;//只选1个数
for(int j=1;j<i;j++)
if(a[j]<a[i])//判断能不能再延长序列
f[i]=max(f[i],f[j]+1);
res=max(res,f[i]);//统计
}
cout<<res;
return 0;
}
完awa~
又水了一篇博客
如果觉得不错就点个赞吧，您的支持是本蒟蒻最大的动力。
