堆排序复习
堆,实际上是一颗完全二叉树,且满足性质:其根节点的关键字不小于(或不大于)其左右孩子节点。
即满足key[i]>=key[2i+1]&&key[i]>=key[2i+2]的称为大根堆;满足key[i]<=key[2i+1]&&key[i]<=key[2i+2]的称为小根堆()。
以大根堆为例,堆排序算法就是利用了堆的根节点一定是堆中最大的数的结构特点,每次将根节点的关键字和最后一个节点交换,从而得到已排序的部分,和未排序的剩余部分,再将剩余部分调整为堆,重新得到根节点,如此递归调用,直到堆中所有元素已然有序。
举个例子,下图为一个5个节点的堆的排序过程(从左至右,从上至下):
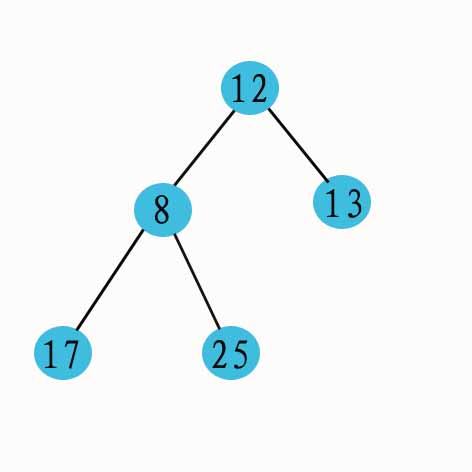
图1为初始大根堆,首先根节点与最后一个节点交换,25为已排序列;之后对剩下的4个节点调整成堆,如图3;将堆顶的17与最后一个节点8交换得到图4;再对剩余的3个节点进行对调整,得到图5;交换堆顶的13和最后一个节点12,得到图6;由于剩下的两个节点已经是一个堆了,所以不用堆调整,直接将堆顶的12与8交换,得到最终的已排序序列,如图7所示,最后将结果输出即可:






测试代码如下:
1 #include <iostream> 2 #include <algorithm> //使用swap函数 3 4 using namespace std; 5 6 void HeapAdjust(int *a,int i,int size) //堆调整函数 7 { 8 int lchild = 2*i+1; //i节点的左孩子节点 9 int rchild = 2*i+2; //i节点的右孩子节点,这里节点号从0开始 10 int max = i; 11 if(i<=(size-1)/2) //若节点不为也叶节点则必须做出调整,否则什么也不做 12 { 13 if(lchild<=(size-1)&&a[lchild]>a[max]) //若左孩子比根节点的关键字大则max指向左孩子 14 { 15 max=lchild; 16 } 17 if(rchild<=(size-1)&&a[rchild]>a[max]) //若右孩子比根节点的关键字大则max指向右孩子 18 { 19 max=rchild; 20 } 21 if(max!=i) //只要最大的不是根节点则与根节点交换 22 { 23 swap(a[i],a[max]); //交换 24 HeapAdjust(a,max,size); //对剩下的堆重新递归调整 25 } 26 } 27 } 28 29 void BuildHeap(int *a,int size) //建堆 30 { 31 int i; 32 for(i=size/2-1;i>=0;i--) 33 HeapAdjust(a,i,size); 34 } 35 36 void HeapSort(int *a,int size) //排序 37 { 38 int i; 39 BuildHeap(a,size); 40 for(i=size-1;i>=0;i--) 41 { 42 swap(a[0],a[i]);
43
44 HeapAdjust(a,0,i); //交换后将剩余元素调整成堆 45 } 46 } 47 48 int main(int argc,char *argv[]) 49 { 50 int a[]={17,12,5,8,40,30,22,19,30,27,13,7}; 51 int i; 52 HeapSort(a,12);
53 for(i=0;i<12;i++) 54 printf("%d\t",a[i]); 55 printf("\n"); 56 57 return 0; 58 }
经验证排序结果正确,另外说一句,由于排序中相同关键字的元素可能被交换,所以堆排序为不稳定排序,其时间复杂度为O(nlogn)。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号