信号与系统——周期信号的傅里叶变换
已知周期矩形脉冲信号 的幅度为
,脉宽为
,周期为
,角频率为
,如下图所示:
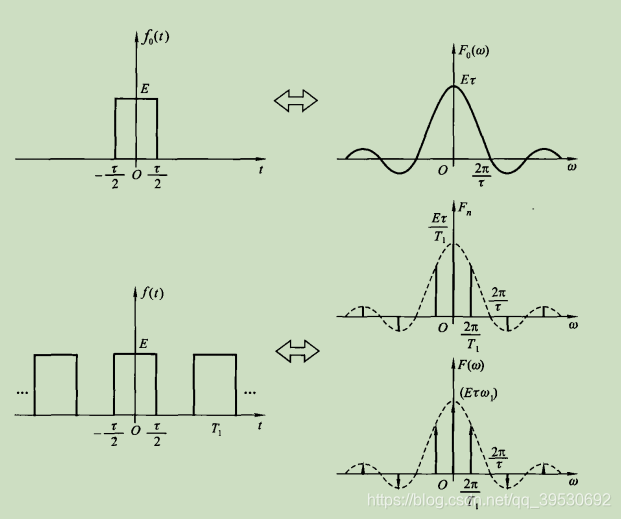
求出该周期矩形脉冲信号的傅里叶级数与傅里叶变换。
首先我们知道矩形脉冲 的傅里叶变换
等于
,根据
所以我么可以求出周期矩形脉冲信号的傅里叶级数 ,所以
所以可以得到 的傅里叶级数为
根据周期信号的傅里叶级数为
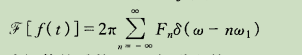
可得到
已知周期矩形脉冲信号 的幅度为
,脉宽为
,周期为
,角频率为
,如下图所示:

求出该周期矩形脉冲信号的傅里叶级数与傅里叶变换。
首先我们知道矩形脉冲 的傅里叶变换
等于
,根据
所以我么可以求出周期矩形脉冲信号的傅里叶级数 ,所以
所以可以得到 的傅里叶级数为
根据周期信号的傅里叶级数为
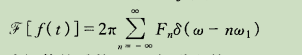
可得到
