信号与系统——抽样信号的傅里叶变换
引言
首先我们要知道什么是抽样信号,抽样信号对于信号的分析和处理有什么作用?我们能用它解决什么样的问题?这些是我们要学习的重点。
什么是抽样?
抽样就是指利用所谓的抽样脉冲序列 从连续信号
中“抽取”一系列的离散样值,我们把这种离散信号称为抽样信号,以
表示。如下图所示:
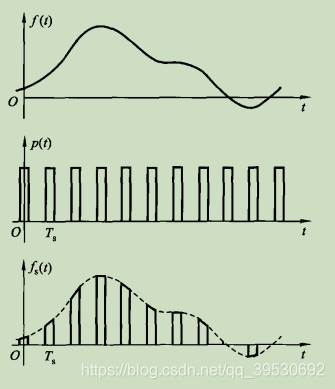
对于我们而言,我们经常把 称为抽样函数,与这里所指的“抽样”或者“抽样信号”具有完全不同的含义。此外,这里的抽样也称为“采样”或“取样”。
抽样用来做什么?
我们通常对一个连续的信号进行抽样,使其变为抽样信号,然后再经量化、编码变成数字信号。这种数字信号经传输,然后进行上述过程的逆变换就可以恢复出原连续信号。
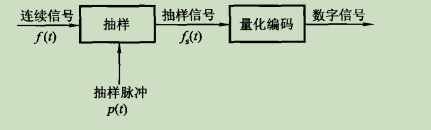
就是说我们对模拟信号进行采样,就可以变成抽样信号,对抽样信号进行量化,就可以变成数字信号。
抽样信号的作用
假设一个模拟信号如下图所示:

我们知道自然界的信号都是模拟信号,但计算机不能直接处理模拟信号,计算机只能处理数字信号,并且只能处理有限长度的数据。因此,我们需要将模拟信号转换成数字信号,这就需要对其进行采样。
一般来说,采样越多,则与原信号与接近,但是我们要在尽可能获取少的值得同时又使其能恢复到原信号,这里面就牵扯到失真的问题。对于在不同的采样率下,信号的幅值是不同的,采样率越高,信号幅值失真越小。



