2019中山纪念中学夏令营-Day21[JZOJ]

2019中山纪念中学夏令营-Day21[JZOJ]

　　提高组（B组模拟赛）Team_B

（由于本人太弱，并没有订正完题目）

（题解大部分是从官方题解文件上摘来的）

日常膜拜大神：じやゆん蒟蒻

 

正文部分：

T1：最小比例（JZOJ3514） Time Limits: 1000 ms  Memory Limits: 131072 KB

 

Description

图中共有N个点的完全图，每条边都有权值，每个点也有权值。要求选出M个点和M-1条边，构成一棵树，使得：



即所有边的权值与所有点的权值之和的比率最小。 

给定N和M，以及N个点的权值，和所有的边权，要求M个点的最小比率生成树。
 

Input

第一行包含两个整数N和M(2<=N<=15，2<=M<=N)，表示点数和生成树的点数。 

接下来一行N个整数，表示N个点的边权。 

最后N行，每行N列，表示完全图中的边权。所有点权和边权都在[1,100]之间。

Output

输出最小比率生成树的M个点。当答案出现多种时，要求输出的第一个点的编号尽量小，第一个相同，则第二个点的编号尽量小，依次类推，中间用空格分开。编号从1开始。
 

Sample Input

输入1：

3 2

30 20 10

0 6 2

6 0 3

2 3 0

输入2：

2 2

1 1

0 2

2 0

Sample Output

输出1：

1 3

输出2：

1 2
 

Data Constraint

对于30%数据，N<=5。

题解&思路：

官方题解：

这是一个相对简单的题。由于n很小，所以直接用递归的方法枚举所有C(n,m)种m个点的取法，对于每一种取法构成的子图，求其最小生成树，记录边权和比点权和最小的那棵树即可。

这个题是2008年ACM亚洲区北京站的简单题。作为NOIP模拟的第一题代码量有一些高，还有，那30%的数据，也只是为枚举边而设计，有些牵强，最小生成树算法对大家应该不是问题。

但是现场264次提交，仅仅通过71队的情况，可以看出，这题也是有一个小陷阱，希望引起大家注意的：实数精度的问题。看似数值不大的两个整数相除，即使double直接相除，也会出现浮点精度误差。如果碰到这类需要比较实数除的情况，可以采用保留分子分母，或者设置一个较小eps=1e-8当做0的情况。此题中，n较大的数据都是用浮点除法和交叉相乘两个程序对拍生成的。

详解：

我们可以先用一个电风扇（DFS）来枚举选m个点的情况

对于电风扇枚举完的每m个点，我们对这m个点跑一遍最小生成树，即可求得答案。

原理：

题目要求 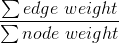最小，而我们枚举完m个点后，这m个点的node weight是固定的（点已经确定了），分母确定了，就让分子尽量小就行了（即跑一遍最小生成树）

代码：

 

 1 #include <cstdio>
 2 #include <algorithm>
 3 #define rr register
 4 using std::sort;
 5 int choose[20],pw[20],head[20],n,m,tot,minn[20],fa[20],a[20][20];
 6 long long minpw=1,minew=0x3f3f3f3f;
 7 struct Edge{
 8     int to,nxt,w,from;
 9 }edge[405];
10 void add(int x,int y,int length)
11 {
12     tot++;
13     edge[tot].to=y;
14     edge[tot].w=length;
15     edge[tot].nxt=head[x];
16     edge[tot].from=x;
17     head[x]=tot;
18 }
19 int getfa(int x)
20 {
21     if(fa[x]==x)
22         return x;
23     return fa[x]=getfa(fa[x]);
24 }
25 bool cmp(Edge x,Edge y)
26 {
27     return x.w < y.w;
28 }
29 void kruskal()
30 {
31     int edgeweight=0;
32     int pointweight=0;
33     for(rr int i=1;i<=n;i++)
34         fa[i]=i;
35     tot=0;
36     for(rr int i=1;i<=m;i++)
37         for(rr int j=1;j<=m;j++)
38         {
39             if(i == j)
40                 continue;
41             add(pw[i],pw[j],a[pw[i]][pw[j]]);
42         }
43     for(rr int i=1;i<=m;i++)
44         pointweight+=choose[pw[i]];
45     sort(edge+1,edge+tot+1,cmp);
46     int num=0;
47     for(rr int i=1;num != m-1;i++)
48     {
49         int x=getfa(edge[i].from) ,y=getfa(edge[i].to);
50         if(x != y)
51         {
52             fa[x]=getfa(y);
53             num++;
54             edgeweight+=edge[i].w;
55         }
56     }
57     if(edgeweight*minpw < minew*pointweight)
58     {
59         minpw=pointweight;
60         minew=edgeweight;
61         for(rr int i=1;i<=m;i++)
62             minn[i]=pw[i];
63     }
64 }
65 void dfs(int x,int k)
66 {
67     if(k == m+1)
68     {
69         kruskal();
70         return;
71     }
72     if(x > n)
73         return ;
74     pw[k]=x;
75     dfs(x+1,k+1);
76     dfs(x+1,k);
77 }
78 signed main()
79 {
80     freopen("ratio.in","r",stdin);
81     freopen("ratio.out","w",stdout);
82     scanf("%d %d",&n,&m);
83     for(rr int i=1;i<=n;i++)
84         scanf("%d",&choose[i]);
85     for(rr int i=1;i<=n;i++)
86         for(rr int j=1;j<=n;j++)
87             scanf("%d",&a[i][j]);
88     dfs(1,1);
89     sort(minn+1,minn+m+1);
90     for(rr int i=1;i<=m;i++)
91         printf("%d ",minn[i]);
92 }

 

 

 T2 软件公司(JZOJ3515) Time Limits: 1000 ms  Memory Limits: 131072 KB 

Description

一家软件开发公司有两个项目，并且这两个项目都由相同数量的m个子项目组成，对于同一个项目，每个子项目都是相互独立且工作量相当的，并且一个项目必须在m个子项目全部完成后才算整个项目完成。

这家公司有n名程序员分配给这两个项目，每个子项目必须由一名程序员一次完成，多名程序员可以同时做同一个项目中的不同子项目。

求最小的时间T使得公司能在T时间内完成两个项目。
 

Input

第一行两个正整数n，m（1<=n<=100,1<=m<=100)。

接下来n行，每行包含两个整数，x和y。分别表示每个程序员完成第一个项目的子程序的时间，和完成第二个项目子程序的时间。每个子程序耗时也不超过100。

Output

输出最小的时间T。
 

Sample Input

3 20

1 1

2 4

1 6

Sample Output

18

【样例解释】

第一个人做18个2项目，耗时18；第二个人做2个1项目，2个2项目耗时12；第三个人做18个1项目，耗时18。
 

Data Constraint

对于30%的数据，n<=30.

对于60%的数据，n<=60.

思路&题解:

官方题解：

普通的动态规划应该比较容易发现。

f[i][j][k]表示前i个人，完成了j个1项目，k个2项目。转移为：

f[i][j][k]=max{f[i][j-s][k-t],s*A[i]+t*B[i]}，不过一算复杂度O(n*m^4),只能通过30%的数据。

开始优化，再分析一下题目和样例。为什么不能是17？在17时，第二个人就会耗时18。想到这里应该不难发现，耗时小于18都是不可行的，大于等于18都是存在可行方案的，耗时最多的人的时间最小。答案是线性的。

二分这个答案！在最大时间已知的情况下，f[i][j][k]就可以用bool表示成是否能在答案内完成。这时，转移的时候就不需要两个项目都枚举了。只要枚举一个，另外一个的最大值会自动产生。转移少了一维，复杂度变为O(n*m^3*log10000)。60%的数据。

优化到这里，也可以有一些感觉，f[i][j][k]就用来表示0,1两种值，是否有些浪费？直接将第三维体现在状态值里面，改造一下状态：

f[i][j]代表到前i个人，在1项目做了j个的情况下，2项目能做的最多的个数。转移为：

 

这样，时间复杂度就O（n*m^2*log(10000))。可以通过所有数据。

 这是一道2004年ACM亚洲区德黑兰站的预赛题。可能比较老的题目了。拿出这个题目想和大家一起探讨一下近几年NOIP题中出现的一个较热门的思想，二分答案！10年的关押罪犯，11年的聪明的质监员，12年的借教室，都有二分答案的方法。而且都是区分水平的关键题。

我们可以总结一下，当碰到所求问题是最小值最大，最大值最小，答案存在线性的临界点的时候，我们都可以二分这个答案，然后根据二分的值设计判断答案可行性的函数。

 我的思路：

（其实我也是按官方题解的思路打的）

代码实现：

 1 #include <cstdio>
 2 #define rr register
 3 const int inf = (1<<30);
 4 int n,m,a[105],b[105],f[105][105];
 5 int max(int x,int y)
 6 {
 7     if(x > y)
 8         return x;
 9     return y;
10 }
11 int binarysearch(int l,int r)
12 {
13     if(l > r)
14         return l;
15     int mid = (l+r)/2;
16     for(rr int i=0;i<=n;i++)
17     {
18         for(rr int j=1;j<=m;j++)
19             f[i][j]=-inf;
20         f[i][0]=0;
21     }
22     for(rr int i=1;i<=n;i++)
23         for(rr int j=0;j<=m;j++)
24             for(rr int k=0;k<=j;k++)
25                 if(k*a[i] <= mid)
26                     f[i][j]=max(f[i][j],f[i-1][j-k]+(mid-k*a[i])/b[i]);
27     if(f[n][m] >= m)
28         return binarysearch(l,mid-1);
29     return binarysearch(mid+1,r);
30 }
31 signed main()
32 {
33     freopen("company.in","r",stdin);
34     freopen("company.out","w",stdout);
35     scanf("%d %d",&n,&m);
36     for(rr int i=1;i<=n;i++)
37         scanf("%d %d",&a[i],&b[i]);
38     printf("%d",binarysearch(1,10025));
39 }

 

T3 空间航行（JZOJ3517） Time Limits: 1000 ms  Memory Limits: 262144 KB

 

Description

你是一艘战列巡洋舰的引擎操作人员，这艘船的船员在空间中侦测到了一些无法辨识的异常信号。你的指挥官给你下达了命令，让你制定航线，驾驶战列巡洋舰到达那里。

船上老旧的曲速引擎的速度是0.1AU/s。然而，在太空中分布着许多殖民星域，这些星域可以被看成一个球。在星域的内部，你可以在任何地方任意次跳跃到星域内部的任意一个点，不花费任何时间。

你希望算出到达终点的最短时间。

 

 

 

Input

输入包含多组测试数据。

对于每一组数据，第一行包含一个正整数n，表示殖民星域的数量。

接下来n 行，第i 行包含四个整数Xi，Yi，Zi，Ri，表示第i个星域的中心坐标为(Xi, Yi,Zi)，星域的半径是Ri。

接下来两行，第一行包含值Xa，Ya，Za，告诉你当前坐标为(Xa, Ya,Za)。

第二行包含值Xo，Yo，Zo，告诉你目的地坐标为(Xo, Yo,Zo)。

输入以一行单独的-1 结尾。所有坐标的单位都是天文单位（AU）。

Output

对于每一组输入数据，输出一行表示从目前的位置到达指定目的地的最短时间，取整到最近整数。输入保证取整是明确的。

 

 

 

Sample Input

1

20 20 20 1

0 0 0

0 0 10

1

5 0 0 4

0 0 0

10 0 0

-1

Sample Output

100

20

 

 

 

Data Constraint

每个输入文件至多包含10 个测试数据。

对于10% 的数据，n = 0。

对于30% 的数据，0<=n<=10。

对于100% 的数据，0<=n<=100，所有坐标的绝对值<=10000 ，半径r<=10000。

你可以认为，你所在的星区的大小为无限大。

 

题解&思路：

官方题解：

100% 的算法 易知，在两个球的之间航行的时间等于两个球心之间的距离减去两个球的半径。 将每个球的球心当作点建图，然后运行最短路算法即可。 无论是 Floyd 算法还是 Dijkstra 算法都可以在限定时间内解决。需要注意的是不要弄出负 的航行时间。

本人思路（详解）

这道题可以先把起点和终点预处理成一个星系（半径为零）

然后跑一遍起点到终点的最短路即可（由于数据范围太水，Floyed也可以过）

如何求各个星系间的最短路：

1.转换成图

　　计算出每个星系到其他所有星系的距离，然后令该星系和其他所有星系间加一条边权为它们距离的边，图的转化就完成了。

距离计算公式：

 

 

 

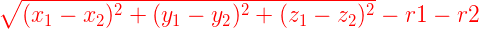
 当然，当两个星系有交集时，这个距离求出来是负的，这时我们就要将两星系间的距离设为0，再跑最短路。

即综合式子：

另外一个细节性问题：

题目要求取整到最近的整数，而C++自带的只有向下取整，因此，要自己用代码实现这个功能。

代码实现：

 1 #include <cstdio>
 2 #include <queue>
 3 #include <algorithm>
 4 #include <cmath>
 5 #include <cstring>
 6 #define rr register
 7 int x[105],y[105],z[105],r[105],n;
 8 using namespace std;
 9 double map[105][105];
10 int changed(double a)//四舍五入
11 {
12     int b=a;
13     double c=a-b;
14     if(c < 0.5)
15         return b;
16     else
17         return b+1;
18 }
19 signed main()
20 {
21     freopen("warp.in","r",stdin);
22     freopen("warp.out","w",stdout);
23     while(1)
24     {
25         scanf("%d",&n);
26         if(n == -1)
27             return 0;
28         for(rr int i=1;i<=n;i++)
29         {
30             scanf("%d %d %d %d",&x[i],&y[i],&z[i],&r[i]);
31         }
32         for(rr int i=n+1;i<=n+2;i++)
33         {
34             scanf("%d %d %d",&x[i],&y[i],&z[i]);
35             r[i]=0;
36         }
37         for(rr int i=1;i<=n+2;i++)
38             for(rr int j=1;j<=n+2;j++)
39             {
40                 map[i][j]=sqrt((x[i]-x[j])*(x[i]-x[j])+(y[i]-y[j])*(y[i]-y[j])+(z[i]-z[j])*(z[i]-z[j]))-r[i]-r[j];
41                 if(map[i][j] < 0)
42                     map[i][j]=0;
43             }
44         n+=2;
45         for(rr int k=1;k<=n;k++)
46             for(rr int i=1;i<=n;i++)
47                 for(rr int j=1;j<=n;j++)
48                     if(map[i][j] > map[i][k]+map[k][j])
49                         map[i][j]=map[i][k]+map[k][j];
50         map[n-1][n]*=10;
51         printf("%d\n",changed(map[n-1][n]));
52     }
53 }

 T4 摧毁巴士站（JZOJ3516）Time Limits: 1000 ms  Memory Limits: 131072 KB

Description

Gabiluso是最伟大的间谍之一。现在，他试图完成一个“不可能完成”的使命――减缓Colugu的军队到达机场的时间。Colugu有n个公共汽车站和m条道路。每条道路直接连接两个巴士站，所有的道路都是单向的。为了保持空气洁净，政府禁止所有军用车辆，因此，军队必须乘搭巴士去机场。两个巴士站之间，可能有超过一条道路。如果一个公共汽车站被破坏时，所有连接该站的道路将无法运作。Gabiluso需要做的是摧毁了一些公共汽车站，使军队无法在K分钟内到达机场。一辆公交车通过一条道路，都是一分钟。所有巴士站的编号从1到n。1号巴士站是在军营，第n号站是机场。军队始终从第一站出发。第一站和第n站不能被破坏，这里有大量的防御力量。当然也没有从第一站到第n站的道路。

请帮助Gabiluso来计算能完成使命所需摧毁的最低数目的巴士站。
 

Input

第一行包含三个整数n，m，k (2<n<=50,0<m<=4000,0<k<1000)。

接下来m行，每行2个整数s和f，表示从站s到站f有一条路。

Output

输出最少需要摧毁的巴士站数目。
 

Sample Input

5 7 3 

1 3 

3 4 

4 5 

1 2 

2 5 

1 4 

4 5

Sample Output

2
 

Data Constraint

30%的数据N<=15。

JZOJ官方题解：

这是一个存在多种解法的题目。本题存在比较复杂的网络流解法，但用此法来解此题颇为小题大做，浪费了赛场上的很多时间。因为，计算时间复杂度可以看出，如果使用网络流来做此题，复杂度大约为O（nm），那么出题者完全可以增大数据范围，而实际数据范围仅为n<=50，这个数据范围暗示着此题是经过优化和剪枝的搜索算法能够通过的题。

最朴素的搜索方法是枚举所有删除点的方案，每找到一种方案，就求一次从1号点到n号点的最短路径，看看其长度是否超过k。每个点有删除和不删除两种状态，所以方案总数最多就是2^48种。这样的搜索时非常盲目的，显然会导致超时。

解决办法是有选择性的进行删点。基本的思路就是，一条长度不超过k的最短路径上的点，至少有一个是要被删掉的（至于删除哪个好，可以枚举尝试），删掉一个点后再重新求最短路，如果新求出的最短路径长度仍然不超过k，那么就在新的最短路径上再找出一个点删掉，然后再求最短路径……直到求出的最短路径长度超过k，那么就找到了一个解。但这个解未必是最优的，所以要用递归的方法搜索多组解，以确保能搜到最优解。具体步骤如下。

递归进行下列操作：

  1. 寻找起点到终点的最短路径，如果最短路径长度超过k，则表示已找到一种删点方案。记录该方案下的删点数目，回溯再找出下一种方案；否则进入下一步。
  2. 枚举最短路径中的除1号点和n号点外的某一个点，将其删除。
  3. 回到1递归继续搜索。

这样的搜索顺序使得枚举的点的数量得到控制。搜索的每一层会从L-2个点中选择一个进行删除，L是当前找到的最短路径的长度。如果当前找到的最短路径很长，虽然在这一层我们需要枚举很多个点进行删除，但也说明起点到终点的距离已经很长了，我们离答案已经很接近了。一般来说，在50个点的图中，答案应该不超过20。那么L<20。并且L比较大的情况只会出现在搜索的最后几层。这么想来，这个搜索的时间复杂度是可以接受的。

当然，我们还可以通过一些其他的方法优化这个搜索。在上述方法中，还可以用迭代加深的方法来搜索。也就是说，先找到删除1个点的方案，看是否存在；如果不存在，则再找到删除2个点的方案；如果还是不存在，则继续找到删除3个点的方案……由于删除的点数增加1，搜索的范围就会成倍增长，虽然这样看似重复搜索了很多遍，但实际上搜索的深度（删除的点数）是有限的，因此搜索的总范围不会非常大。实际测试的结果表明，使用迭代加深的方法搜索能够缩短很多的时间。

       以上是出题人的原版题解。这个题目同样是ACM08年北京站的题目，现场赛25次提交，4队通过，应该是难题了。其实，对OIer来说，搜索的技巧更是需要不断通过难题来积累的。记得以前常问不少大神，某某题是怎么做的，无数次得到的回答是：暴搜！当然，此暴搜肯定是经过了许多的优化，而这些优化在高手日积月累的搜索技巧面前就是家常便饭了。在OI中，同样的题目，都采用搜索，有些就只能拿基本分，而有些就可以拿下大部分，甚至AC，这种情况很常见。搜索技巧在很多时候也成了区分OI选手水平的重要标志。要提高也只能通过不断的做题，了解不同类型题目的搜索剪枝技巧，还有就是尝试一些IDDFS，A*等不同的搜索方式。水平有限，也希望大神们可以总结一些好的搜索攻略。

       这题还可以用最小割的做法，图论熟练的同学，应该比较容易想到。广搜之后，求起点到终点的点割集即可。每个点权为1，转为边权后最大流即可。

       此题数据不是官方的，可能不太全面，请大家谅解。

本人思路：电风扇（DFS）+不分手（BFS）（咕咕咕）

代码实现：

咕咕咕

posted @ 2019-08-22 11:34  XYYXP  阅读(483)  评论(0)  编辑  收藏  举报