（二） Keras 非线性回归

视频学习来源

https://www.bilibili.com/video/av40787141?from=search&seid=17003307842787199553

笔记

Keras 非线性回归

import keras

import numpy as np

import matplotlib.pyplot as plt

#Sequential按序列构成的模型

from keras.models import Sequential

#Dense全连接层

from keras.layers import Dense

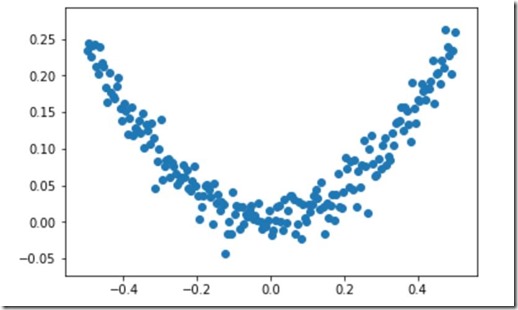
#使用numpy生成200个随机点

x_data=np.linspace(-0.5,0.5,200)  #均匀分布

noise=np.random.normal(0,0.02,x_data.shape)  #均值为0，方差为0.02

y_data=np.square(x_data)+noise

#显示随机点

plt.scatter(x_data,y_data)

plt.show()

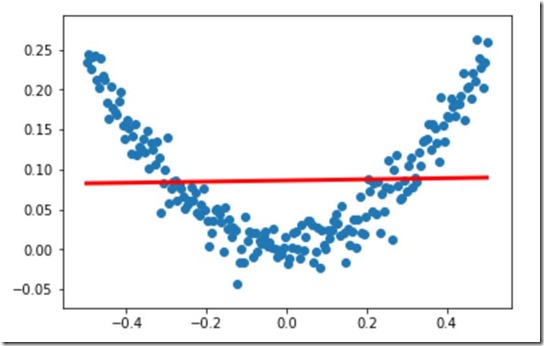
#构建一个顺序模型
model=Sequential()
#在模型中添加一个全连接层
model.add(Dense(units=1,input_dim=1))

#sgd:stochastic gradient descent 随机梯度下降算法
#mse：mean square error 均方误差
model.compile(optimizer='sgd',loss='mse')

#训练3000次
for step in range(3000):
    #每次训练一个批次
    cost=model.train_on_batch(x_data,y_data)
    #每500个batch打印一次cost值
    if step%500==0:
        print('cost:',cost)
        
#x_data输入网络中，得到预测值y_pred
y_pred=model.predict(x_data)

#显示随机点
plt.scatter(x_data,y_data)
#显示预测结果
plt.plot(x_data,y_pred,'r-',lw=3)
plt.show()

cost: 0.018438313

cost: 0.006655791

cost: 0.0058503654

cost: 0.0057009794

cost: 0.0056732716

cost: 0.005668133

加入隐藏层

#导入SGD,(后面要修改SGD的值)
from keras.optimizers import SGD

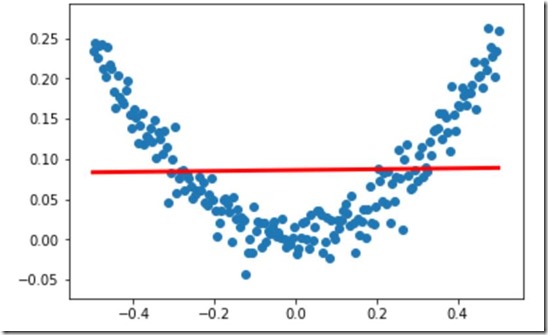
#构建一个顺序模型
model=Sequential()
#在模型中添加  1-10-1  ,一个输入，一个输出，中间10个隐藏层
model.add(Dense(units=10,input_dim=1))   #1-10部分
model.add(Dense(units=1)) #10-1部分 等效 model.add(Dense(units=1,input_dim=10))


#增大sgd算法的学习率，默认值为0.01，
#查看函数默认值可在jupyter中shift+Tab+Tab，前提是已经导入
sgd=SGD(lr=0.3)   #学习速率0.3


#sgd:stochastic gradient descent 随机梯度下降算法
#mse：mean square error 均方误差
model.compile(optimizer=sgd,loss='mse')   #和上面不同的是没有引号

#训练3000次
for step in range(3000):
    #每次训练一个批次
    cost=model.train_on_batch(x_data,y_data)
    #每500个batch打印一次cost值
    if step%500==0:
        print('cost:',cost)
        
#x_data输入网络中，得到预测值y_pred
y_pred=model.predict(x_data)

#显示随机点
plt.scatter(x_data,y_data)
#显示预测结果
plt.plot(x_data,y_pred,'r-',lw=3)
plt.show()

cost: 0.1012776

cost: 0.005666962

cost: 0.005666963

cost: 0.0056669624

cost: 0.005666963

cost: 0.005666963

设置激活函数

#设置激活函数，默认的激活函数为none也就是输入=输出，线性
from keras.layers import Dense,Activation

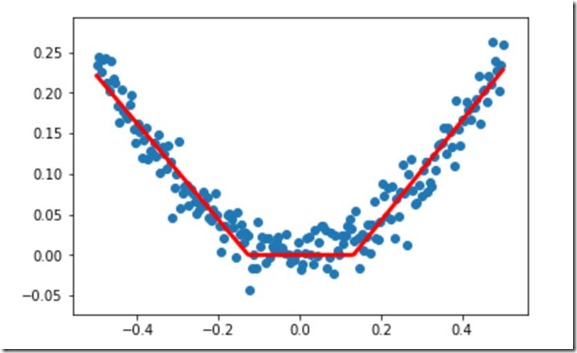
#设置激活函数方式1
#激活函数为tanh

#构建一个顺序模型
model=Sequential()
#在模型中添加  1-10-1  ,一个输入，一个输出，中间10个隐藏层
model.add(Dense(units=10,input_dim=1))   #1-10部分

model.add(Activation('tanh'))  #双曲正切函数

model.add(Dense(units=1)) #10-1部分 等效 model.add(Dense(units=1,input_dim=10))

model.add(Activation('tanh'))  #双曲正切函数

#增大sgd算法的学习率，默认值为0.01，
#查看函数默认值可在jupyter中shift+Tab+Tab，前提是已经导入
sgd=SGD(lr=0.3)   #学习速率0.3

#sgd:stochastic gradient descent 随机梯度下降算法
#mse：mean square error 均方误差
model.compile(optimizer=sgd,loss='mse')   #和上面不同的是没有引号

#训练3000次
for step in range(3000):
    #每次训练一个批次
    cost=model.train_on_batch(x_data,y_data)
    #每500个batch打印一次cost值
    if step%500==0:
        print('cost:',cost)
        
#x_data输入网络中，得到预测值y_pred
y_pred=model.predict(x_data)

#显示随机点
plt.scatter(x_data,y_data)
#显示预测结果
plt.plot(x_data,y_pred,'r-',lw=3)
plt.show()

cost: 0.049393196

cost: 0.003914159

cost: 0.0011130853

cost: 0.00090270495

cost: 0.00040989672

cost: 0.00045533947

#设置激活函数方式2
#激活函数为relu

#jupyter中 注释为 ctrl+/ 

#构建一个顺序模型
model=Sequential()
#在模型中添加  1-10-1  ,一个输入，一个输出，中间10个隐藏层
model.add(Dense(units=10,input_dim=1,activation='relu'))   #1-10部分  

model.add(Dense(units=1,activation='relu'))#10-1部分 等效 model.add(Dense(units=1,input_dim=10))

#增大sgd算法的学习率，默认值为0.01，
#查看函数默认值可在jupyter中shift+Tab+Tab，前提是已经导入
sgd=SGD(lr=0.3)   #学习速率0.3

#sgd:stochastic gradient descent 随机梯度下降算法
#mse：mean square error 均方误差
model.compile(optimizer=sgd,loss='mse')   #和上面不同的是没有引号

#训练3000次
for step in range(3000):
    #每次训练一个批次
    cost=model.train_on_batch(x_data,y_data)
    #每500个batch打印一次cost值
    if step%500==0:
        print('cost:',cost)
        
#x_data输入网络中，得到预测值y_pred
y_pred=model.predict(x_data)

#显示随机点
plt.scatter(x_data,y_data)
#显示预测结果
plt.plot(x_data,y_pred,'r-',lw=3)
plt.show()

cost: 0.0066929995

cost: 0.0004892901

cost: 0.00047061846

cost: 0.00046780292

cost: 0.00046706214

cost: 0.00046700903

shift+Tab+Tab 效果如下