希尔排序
/**
* 希尔排序————和折半插入排序法一样,也是直接插入排序的改进版
* 1959年Shell发明,较早突破O(n2)的排序算法。它与插入排序的不
* 同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
* 其最坏时间复杂度依然为O(n2),一些经过优化的增量序列如Hibbard经过复杂证明可使得最坏时间复杂度为O(n3/2)。
* <p>
* 思想:将数组分为几个区,然后在每个区内排序,然后将区数缩小,再次迭代
*/
1 public int[] shellSort(int[] a) {
2 for (int gap = a.length / 2; gap > 0; gap /= 2) {//增量每次都/2, 但是并非是最优解
3 //从增量那组开始进行插入排序,直至完毕 (gap即是当前组数)
4 for (int i = gap; i < a.length; i++) { // 可能不太理解为什么是从i=gap开始,为什么i要到a.length-1才停,看下面的例子
5 int temp = a[i];
6 int j;
7 // j - gap 就是代表与它同组隔壁的元素
8 for (j = i; j - gap >= 0 && a[j - gap] > temp; j -= gap) {
9 a[j] = a[j - gap];
10 }
11 a[j] = temp;
12 }
13 }
14 return a;
15 }
假如有一个9元数组:

假如 gap = 3
那么分为3组
每组3个元素
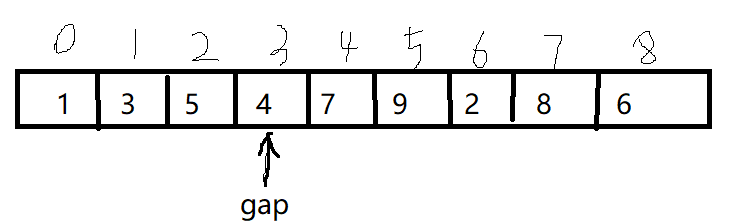
那么,这三组的元素分别是:

在每个组组内,分别进行直接插入排序
第一组:
| 0 | 3 | 6 |
| 1 | 4 | 2 |
从第二个元素开始,也就是从gap下标开始,依次与前面的元素比对,然后插入,可见,要进行两次插入
第二组和第三组也是一样的,只是开始的位置分别是,gap+1,gap+2
那么总共要比对-插入6次,也就是a.length-gap次
不过,需要注意的是,每组的“比对-插入”是交替进行的,按1,2,3,1,2,3,1,2,3进行,而不是按我们想的那样,每组一次就进行插入排序排好
所以解释了上面这条语句:
性能分析:
时间复杂度:大概在 O(n^(1.5))左右,不同的优化不同,后面我会将所有的排序方法来个大比对,就一目了然了
空间复杂度:O(1)
稳定性:不稳定 (通过分组的方法,是及其不稳定的)


