杂题选谈

E. Another Minimum Spanning Tree

http://222.180.160.110:1024/contest/4940/problem/5

曼哈顿最小距离生成树。给定 \(n\) 个已知坐标的点，两两之间可连权值为曼哈顿距离的边，需求最小生成树。

有一引理：以任意一点为顶点的大小为 \(\dfrac \pi8\) 、且一条边与坐标轴重合的角覆盖的范围中，与该点曼哈顿距离最小的点才有可能与此点连边。

概括说来便是以该点为原点建系，沿坐标轴米字划分。

浅证

首先需认识到，若 \(w(x,y)<w(x,z)\) 且 \(w(y,z)<w(x,z)\)，则边 \(E(x,z)\) 不在最小生成树中。

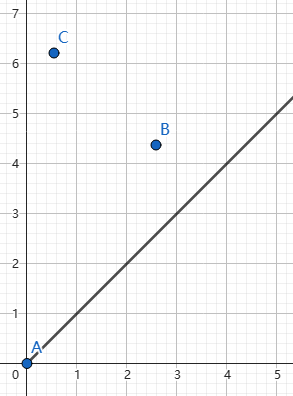
考虑有如上 \(A,B,C\) 三点。不妨设 \(d(A,B)\le d(A,C)\)。其中 \(d\) 为曼哈顿距离。

由图易知 \(x_B,y_B,x_C,y_C>0\) 且 \(y_B-x_B,y_C-x_C>0\)。讨论 \(B\) 与 \(C\) 位置关系。下文的 \(x,y\) 均相对 \(A\) 而言。

• \(x_B>x_C\) 且 \(y_B>y_c\)：

  此时 \(d(A,B)>d(B,C)\)，与题设不符，舍去。

• \(x_B>x_C\) 且 \(y_B<y_C\)：

  此时 \(d(A,B)=x_B+y_B,d(B,C)=x_B-x_C+y_C-y_B,d(A,C)=x_C+y_C\)。由作差法得 \(d(B,C)-d(A,C)=x_B-y_B-2\times x_C\)，由 \(x_B-y_B<0,x_C>0\)，\(d(B,C)<d(A,C)\)。

  由于 \(d(A,B),d(B,C)<d(A,C)\)，故 \(A\) 一定不与 \(C\) 连边。

• \(x_B<x_C\) 且 \(y_B>y_C\)：

  与上一种情况同理。

• \(x_B<x_C\) 且 \(y_B<y_C\)：

  此时有 \(d(A,C)=d(A,B)+d(B,C)\)，则 \(A\) 一定不与 \(C\) 连边。

如此一来，边数便降低到了 \(\mathcal O(n)\) 水平。

此外，如何识别每个点周围每 \(\dfrac \pi8\) 的最近点便是问题所在。

由于坐标可以变换，此处仅考虑顶点为 \(A\)，始边沿 \(y\) 轴正方向，终边沿 \(k=1\) 的区域。则对于区域内的点 \(B\)，易知 \(x_B\geqslant x_A,y_B-y_A\geqslant x_B-x_A\)。

后一条规则分离变量则有 \(y_B-x_B\geqslant y_A-x_A\)，那么问题转化为二维偏序，其中待求为最小 \(x_B+y_B\)，可以用树状数组离散解决。

由于边是双向的，将问题在平面任意连续 \(\dfrac \pi 2\) 范围内进行四次坐标转化即可。

其实并不一定要连续，只要该区域与其旋转一百八十度后的图形的并可以覆盖整个平面即可。这么看来是不是只能连续。

我们会发现旋转 \(\dfrac \pi 8\) 这个我们在整数域上做不到啊。所以我们考虑旋转 + 翻折，最后整出来差不多这个图形：

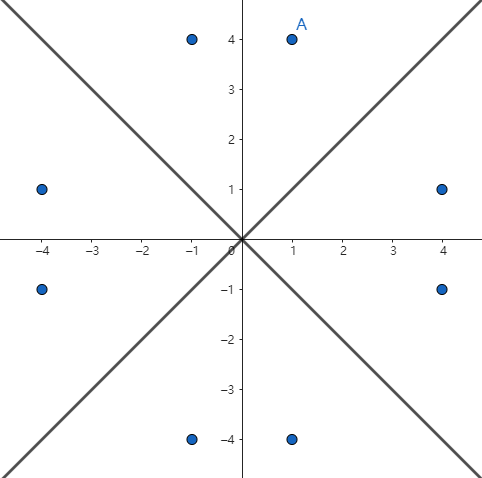
然后由于我们发现这些点关于 \(A\) 的关系（是通过 \(A\) 翻折还是旋转得来的）并不中心对称啊，所以呢就要委屈一下写满八个方向了。

namespace XSC062 {
using namespace fastIO;
const int maxn = 1e5 + 5;
struct _ {
	int x, y, id;
	bool operator< (const _ &q) const {
		return y - x > q.y - q.x;
	}
};
struct __ {
	int x, y, w;
	__() {}
	__(int x1, int y1, int w1) {
		if (y1 < x1) x1 ^= y1 ^= x1 ^= y1;
		x = x1, y = y1, w = w1;
	}
	bool operator< (const __ &q) const {
		return w == q.w ? x < q.x : w < q.w;
	}
};
int n;
int Bit[maxn]; 
std::vector<__> e;
_ a[maxn], b[maxn];
int ls[maxn], f[maxn];
int lowbit(int x) { return x & -x; }
void upd(int &i, int j) {
	if (!i || (j && b[j].x + b[j].y <= b[i].x + b[i].y)) i = j;
	return;
}
void add(int x, int i) {
	for (; x <= n; x += lowbit(x)) upd(Bit[x], i);
	return;
}
int ask(int x) {
	int res = 0;
	for (; x; x -= lowbit(x)) upd(res, Bit[x]);
	return res;
} 
int find(int x) { return x == f[x] ? x : f[x] = find(f[x]); }
void merge(int x, int y) { f[find(x)] = find(y); return; }
int abs(int x) { return x >= 0 ? x : -x; }
void adde(int x, int y) {
	if (!x || !y) return;
	e.emplace_back(x, y, abs(a[x].x - a[y].x) + abs(a[x].y - a[y].y));
	return;
}
int main() {
	read(n);
	while (n) {
		e.clear();
		for (int i = 1; i <= n; ++i) {
			read(a[i].x), read(a[i].y), a[i].id = i;
			ls[i] = a[i].x, b[i] = a[i], f[i] = i;
		}
		memset(Bit, 0, sizeof (Bit));
		std::sort(b + 1, b + n + 1);
		std::sort(ls + 1, ls + n + 1);
		for (int i = 1; i <= n; ++i) {
			int x = std::lower_bound(ls + 1, ls + n + 1, b[i].x) - ls;
			x = n + 1 - x, adde(b[i].id, b[ask(x)].id), add(x, i);
		}
		memset(Bit, 0, sizeof (Bit));
		for (int i = 1; i <= n; ++i) {
			b[i].x = a[i].y, b[i].y = a[i].x;
			ls[i] = b[i].x, b[i].id = i;
		}
		std::sort(b + 1, b + n + 1);
		std::sort(ls + 1, ls + n + 1);
		for (int i = 1; i <= n; ++i) {
			int x = std::lower_bound(ls + 1, ls + n + 1, b[i].x) - ls;
			assert(x >= 1 && x <= n);
			x = n + 1 - x, adde(b[i].id, b[ask(x)].id), add(x, i);
		}
		memset(Bit, 0, sizeof (Bit));
		for (int i = 1; i <= n; ++i) {
			b[i].x = -a[i].x, b[i].y = a[i].y;
			ls[i] = b[i].x, b[i].id = i;
		}
		std::sort(b + 1, b + n + 1);
		std::sort(ls + 1, ls + n + 1);
		for (int i = 1; i <= n; ++i) {
			int x = std::lower_bound(ls + 1, ls + n + 1, b[i].x) - ls;
			assert(x >= 1 && x <= n);
			x = n + 1 - x, adde(b[i].id, b[ask(x)].id), add(x, i);
		}
		memset(Bit, 0, sizeof (Bit));
		for (int i = 1; i <= n; ++i) {
			b[i].x = -a[i].y, b[i].y = a[i].x;
			ls[i] = b[i].x, b[i].id = i;
		}
		std::sort(b + 1, b + n + 1);
		std::sort(ls + 1, ls + n + 1);
		for (int i = 1; i <= n; ++i) {
			int x = std::lower_bound(ls + 1, ls + n + 1, b[i].x) - ls;
			assert(x >= 1 && x <= n);
			x = n + 1 - x, adde(b[i].id, b[ask(x)].id), add(x, i);
		}
		memset(Bit, 0, sizeof (Bit));
		for (int i = 1; i <= n; ++i) {
			b[i].x = -a[i].y, b[i].y = -a[i].x;
			ls[i] = b[i].x, b[i].id = i;
		}
		std::sort(b + 1, b + n + 1);
		std::sort(ls + 1, ls + n + 1);
		for (int i = 1; i <= n; ++i) {
			int x = std::lower_bound(ls + 1, ls + n + 1, b[i].x) - ls;
			assert(x >= 1 && x <= n);
			x = n + 1 - x, adde(b[i].id, b[ask(x)].id), add(x, i);
		}
		memset(Bit, 0, sizeof (Bit));
		for (int i = 1; i <= n; ++i) {
			b[i].x = -a[i].x, b[i].y = -a[i].y;
			ls[i] = b[i].x, b[i].id = i;
		}
		std::sort(b + 1, b + n + 1);
		std::sort(ls + 1, ls + n + 1);
		for (int i = 1; i <= n; ++i) {
			int x = std::lower_bound(ls + 1, ls + n + 1, b[i].x) - ls;
			assert(x >= 1 && x <= n);
			x = n + 1 - x, adde(b[i].id, b[ask(x)].id), add(x, i);
		}
		memset(Bit, 0, sizeof (Bit));
		for (int i = 1; i <= n; ++i) {
			b[i].x = a[i].x, b[i].y = -a[i].y;
			ls[i] = b[i].x, b[i].id = i;
		}
		std::sort(b + 1, b + n + 1);
		std::sort(ls + 1, ls + n + 1);
		for (int i = 1; i <= n; ++i) {
			int x = std::lower_bound(ls + 1, ls + n + 1, b[i].x) - ls;
			assert(x >= 1 && x <= n);
			x = n + 1 - x, adde(b[i].id, b[ask(x)].id), add(x, i);
		}
		memset(Bit, 0, sizeof (Bit));
		for (int i = 1; i <= n; ++i) {
			b[i].x = a[i].y, b[i].y = -a[i].x;
			ls[i] = b[i].x, b[i].id = i;
		}
		std::sort(b + 1, b + n + 1);
		std::sort(ls + 1, ls + n + 1);
		for (int i = 1; i <= n; ++i) {
			int x = std::lower_bound(ls + 1, ls + n + 1, b[i].x) - ls;
			assert(x >= 1 && x <= n);
			x = n + 1 - x, adde(b[i].id, b[ask(x)].id), add(x, i);
		}
		std::sort(e.begin(), e.end());
		int res = 0;
		for (auto i : e) {
			if (find(i.x) != find(i.y))
				res += i.w, merge(i.x, i.y);
		}
		static int TimeKeeper = 0;
		printf("Case %d: Total Weight = %d\n", ++TimeKeeper, res);
		read(n);
	}
	return 0;
}
} // namespace XSC062