230706 // 换根 DP 复习

菌：园什是我笋子

元首：我是你打野

我：元首耳朵得治

G. 求树的重心

http://222.180.160.110:1024/contest/3744/problem/7

我们知道，重心的定义是，将其切除后，每个连通块的大小不超过 \(\dfrac n2\)。连通块分为 其子树 和 整棵树减去该结点引导的子树，所以我们记录 size，在每次搜索结束后判断当前搜索结点的所有子树 size 和 n - siz[x] 是否合法。若都合法则记录答案。

复杂度 \(\mathcal O(n)\)。

namespace XSC062 {
using namespace fastIO;
const int maxn = 105;
int n, x, y;
int siz[maxn];
std::vector<int> res;
std::vector<int> g[maxn];
void DFS(int x, int fa) {
	bool flag = 1;
	siz[x] = 1;
	for (auto i : g[x]) {
		if (i == fa)
			continue;
		DFS(i, x);
		siz[x] += siz[i];
		flag &= (siz[i] <= n / 2);
	}
	flag &= (n - siz[x] <= n / 2);
	if (flag)
		res.push_back(x);
	return;
}
inline void add(int x, int y) {
	g[x].push_back(y);
	return;
}
int main() {
	read(n);
	for (int i = 1; i < n; ++i) {
		read(x), read(y);
		add(x, y), add(y, x);
	}
	DFS(1, -1);
	std::sort(res.begin(), res.end());
	print(res.size(), '\n');
	for (auto i : res)
		print(i, '\n');
	return 0;
}
} // namespace XSC062

H. 树的直径

http://222.180.160.110:1024/contest/3744/problem/8

树的直径，指的是树中最长链。

对于一个点 \(x\)，我们求得其子树中的最长链和次长链，相加即为最长链的一组可能的解。

这个操作处理了全树最长链的最高点是 \(x\) 的情况，所以我们并不用在意 \(x\) 的祖辈，因为对于 \(x\)，只需要在自己以下的高度求解即可，更高的高度会由其他搜索得到答案。

在更新最长链和次长链的时候会有一个 trick：我们只用下级子树的 最长链 来更新上极子树的 最长链 和 次长链，否则会导致下级子树的最长链和次长链可能同时成为上级子树统计的最长链和次长链，导致求得的解包含重复结点。并且，从贪心的角度想，只有最长链才会更新最佳答案，所以这种方案是正确的。

namespace XSC062 {
using namespace fastIO;
const int maxn = 1e5 + 5;
const int inf = 0x3f3f3f3f;
int f[maxn][2];
int n, x, y, res;
std::vector<int> g[maxn];
inline int max(int x, int y) {
	return x > y ? x : y;
}
inline void upd(int x, int u) {
	if (u >= f[x][0]) {
		f[x][1] = f[x][0];
		f[x][0] = u;
	}
	else if (u > f[x][1])
		f[x][1] = u;
	return;
}
void DFS(int x, int fa) {
	f[x][0] = 0, f[x][1] = -inf;
	for (auto i : g[x]) {
		if (i == fa)
			continue;
		DFS(i, x);
		upd(x, f[i][0] + 1);
	}
	res = max(res, f[x][0] + f[x][1]);
	return;
}
inline void add(int x, int y) {
	g[x].push_back(y);
	return;
}
int main() {
	read(n);
	for (int i = 1; i < n; ++i) {
		read(x), read(y);
		add(x, y), add(y, x);
	}
	DFS(1, -1);
	print(res);
	return 0;
}
} // namespace XSC062

I. 没有上司的舞会

http://222.180.160.110:1024/contest/3744/problem/9

简单 DP。设 \(f_{x, 0 / 1}\) 表示 \(x\) 参加 / 未参加下的最大值。

若父节点 \(u\) 未参加，则子节点 \(v\) 可以选择参加或不参加。若 \(u\) 参加，那么 \(v\) 一定不能参加。则有：

\[f_{u, 0} = \sum \max(f_{v, 0}, f_{v, 1}) \\ f_{u, 1} = \sum f_{v, 0} \]

namespace XSC062 {
using namespace fastIO;
const int maxn = 6e3 + 5;
const int inf = 0x3f3f3f3f;
int n, x, y;
int f[maxn][2];
int deg[maxn], a[maxn];
std::vector<int> g[maxn];
inline int max(int x, int y) {
	return x > y ? x : y;
}
void DFS(int x, int fa) {
	f[x][1] = a[x];
	for (auto i : g[x]) {
		if (i == fa)
			continue;
		DFS(i, x);
		f[x][1] += f[i][0];
		f[x][0] += max(f[i][0], f[i][1]);
	}
	return;
}
inline void add(int x, int y) {
	g[x].push_back(y);
	return;
}
int main() {
	read(n);
	for (int i = 1; i <= n; ++i)
		read(a[i]);
	for (int i = 1; i < n; ++i) {
		read(y), read(x);
		add(x, y), ++deg[y];
	}
	for (int i = 1; i <= n; ++i) {
		if (!deg[i]) {
			DFS(i, -1);
			print(max(f[i][0], f[i][1]), '\n');
		}
	}
	return 0;
}
} // namespace XSC062

A. Sta

http://222.180.160.110:1024/contest/3744/problem/1

考虑换根。当 \(v\) 代替 \(u\) 作为根时，\(v\) 引导的子树整体深度 -1，其余点（即原本由 \(u\) 引导的除 \(v\) 外的子树）整体深度 +1，可得：

\[f_v = f_u - s_v + (n - s_v) \]

其中 \(s\) 记录 size。

具体实现的时候会有一个 trick，即当输入一条长为 \(10^6\) 的链时，答案可达到 \(\dfrac {10^6 \times (10^6) + 1}2\)，会爆 int，所以要开龙龙。

整体复杂度 \(\mathcal O(n)\)。

#define int long long
namespace XSC062 {
using namespace fastIO;
const int maxn = 1e6 + 5;
int n, x, y, t;
std::vector<int> g[maxn];
int dep[maxn], siz[maxn], f[maxn];
inline int max(int x, int y) {
	return x > y ? x : y;
}
void DFS1(int x, int fa) {
	siz[x] = 1;
	for (auto i : g[x]) {
		if (i == fa)
			continue;
		dep[i] = dep[x] + 1;
		DFS1(i, x);
		siz[x] += siz[i];
	}
	f[1] += dep[x];
	return;
}
void DFS2(int x, int fa) {
	for (auto i : g[x]) {
		if (i == fa)
			continue;
		f[i] = f[x] - siz[i] + (n - siz[i]);
		DFS2(i, x);
	}
	return;
}
inline void add(int x, int y) {
	g[x].push_back(y);
	return;
}
int main() {
	read(n);
	for (int i = 1; i < n; ++i) {
		read(x), read(y);
		add(x, y), add(y, x);
	}
	dep[1] = 1;
	DFS1(1, -1), DFS2(1, -1);
	for (int i = 1; i <= n; ++i) {
		if (f[i] > f[t])
			t = i;
	}
	print(t, '\n');
	return 0;
}
} // namespace XSC062
#undef int

B. 积蓄程度（加强版）

http://222.180.160.110:1024/contest/3744/problem/2

不难发现，对于一个点，其能接受的水是流入限制和流出总限制中的较小值，根据这一点第一次搜索求得一组特解。

考虑换根。画图可知，发生改变的值只有新根 \(v\) 的流入限制（改为 \(\inf\)）、\(v\) 的流出限制（新增限制 \(E(u, v)\)）、原根 \(u\) 的流入限制（改为 \(E(u, v)\)）、\(u\) 的流出限制（减少 \(E(u, v)\)）。

设 \(t_x\) 为 \(x\) 能接受的水量，则有：

\[f_v = \min(f_u - t_v, E(u, v)) + out_v \]

其中 \(f_u - t_v\) 计算 \(u\) 的流出量，与流入量 \(E(u, v)\) 比较得到 \(u\) 的可接受水量，加上 \(out_v\) 得到 \(v\) 的总流出水量，即总流量。

这里有两个 trick：

  • 当 \(v\) 是 \(u\) 的唯一子节点，换根后 \(u\) 成为叶子，实际上的流出量应为 \(\inf\)，但计算值为 0，需要特判。
  • 当 \(v\) 是叶子时，\(out_v=\inf\)，但换根后 \(v\) 不再是叶子，实际的 \(out_v\) 应按照 0 计算，需要特判。

总时间复杂度 \(\mathcal O(n)\)。

#define int long long
namespace XSC062 {
using namespace fastIO;
const int inf = 1e18;
const int maxn = 2e5 + 5;
struct _ {
	int v, w;
	_() {}
	_(int v1, int w1) {
		v = v1, w = w1;
	}
};
int T, n, x, y, w, res;
std::vector<_> g[maxn];
int in[maxn], out[maxn];
int a[maxn], f[maxn], t[maxn];
inline int min(int x, int y) {
	return x < y ? x : y;
}
inline int max(int x, int y) {
	return x > y ? x : y;
}
inline int f1(int x) {
	return x ? x : inf;
}
inline int f2(int x) {
	return x == inf ? 0 : x;
}
void DFS1(int x, int fa) {
	bool flag = 0;
	for (auto i : g[x]) {
		if (i.v == fa)
			continue;
		flag = 1;
		in[i.v] = i.w;
		DFS1(i.v, x);
		out[x] += t[i.v];
	}
	if (flag == 0)
		out[x] = inf;
	t[x] = min(in[x], out[x]);
	return;
}
void DFS2(int x, int fa) {
	for (auto i : g[x]) {
		if (i.v == fa)
			continue;
		int fx = min(f1(f[x] - t[i.v]), i.w);
		f[i.v] = fx + f2(out[i.v]);
		DFS2(i.v, x);
	}
	res = max(res, f[x]);
	return;
}
inline void add(int x, int y, int w) {
	g[x].push_back(_(y, w));
	return;
}
inline void Init(int n) {
	res = 0;
	for (int i = 1; i <= n; ++i) {
		g[i].clear();
		f[i] = t[i] = in[i] = out[i] = 0;
	}
	return;
}
int main() {
	read(T);
	while (T--) {
		read(n), Init(n);
		for (int i = 1; i < n; ++i) {
			read(x), read(y), read(w);
			add(x, y, w), add(y, x, w);
		}
		in[1] = inf;
		DFS1(1, -1);
		f[1] = t[1];
		DFS2(1, -1);
		print(res, '\n');
	}
	return 0;
}
} // namespace XSC062
#undef int

D. 最大疯子树

http://222.180.160.110:1024/contest/3744/problem/4

听隔壁南通说这是一道猜结论题，好哇，开猜。

首先认识到一点，树的任意连通子图仍是树，且树上任意两点间有且仅有一条简单路径。

考虑最小点 \(b_1\)，对于 \(b_2\)，它和 \(b_1\) 的简单路径中不能有比 \(b_1\) 更大的点，也就是说 \(b_{3\sim m}\) 都不在 \(b_1\) 和 \(b_2\) 之间，说明 \(b_1\) 和 \(b_2\) 由一条边直接相连。

考虑 \(b_3\) 的位置，\(b_3\) 不能在 \(b_1\) 和 \(b_2\) 之间，且 \(b_3\) 和 \(b_2\) 之间不能存在 \(b_{4\sim m}\)，由于树上任意两点之间的路径是唯一的，我们只需要保证 \(b_3\) 和 \(b_1,b_2\) 中的任意一点之间相连即可。

同样地，我们需要保证 \(b_4\) 与 \(b_1,b_2,b_3\) 中的任意一点直接连接。

那么反过来，我们已知一组点 \(b_{1\sim m}\)，怎样将它们编排成一棵树，满足上述要求呢？

先插入 \(b_1\) 并令其为根，插入 \(b_2\) 作为 \(b_1\) 子节点，插入 \(b_3\) 作为 \(b_2\) 或 \(b_1\) 子节点，插入 \(b_4\) 作为 \(b_1\) 或 \(b_2\) 或 \(b_3\) 的子节点…… 我们会发现，在以 \(b_1\) 为根时，每个点的儿子只会比自己大。

那么接下来的处理就很明确了，我们进行换根，统计出以每个点为根时（即让该点成为 \(b_1\)），满足子节点大于父节点的最大 子图。设 \(s_x\) 表示以 1 为根时，\(x\) 的满足条件的最大 子树；\(f_x\) 表示 \(x\) 为根时，满足条件的最大 子图；\(r\) 为递归过程中统计的从该点开始，到 1 方向的最长连续上升长度。则有：

\[f_v = \begin {cases} s_v + s_u + r & (a_x > a_i) \\ s_v & \mbox {otherwise} \end {cases} \]

时间复杂度 \(\mathcal O(n)\)。

#define int long long
namespace XSC062 {
using namespace fastIO;
const int inf = 1e18;
const int maxn = 2e5 + 5;
int T, n, x, y, res;
std::vector<int> g[maxn];
int a[maxn], f[maxn], s[maxn];
inline int max(int x, int y) {
	return x > y ? x : y;
}
void DFS1(int x, int fa) {
	s[x] = 1;
	for (auto i : g[x]) {
		if (i == fa)
			continue;
		DFS1(i, x);
		if (a[i] > a[x])
			s[x] += s[i];
	}
	return;
}
void DFS2(int x, int fa, int r) {
	for (auto i : g[x]) {
		if (i == fa)
			continue;
		int l = 0;
		if (a[x] > a[i])
			l = s[x] + r;
		f[i] = s[i] + l;
		DFS2(i, x, l);
	}
	res = max(res, f[x]);
	return;
}
inline void add(int x, int y) {
	g[x].push_back(y);
	return;
}
inline void Init(int n) {
	res = 0;
	for (int i = 1; i <= n; ++i) {
		g[i].clear();
		f[i] = 0;
	}
	return;
}
int main() {
	while (read(n)) {
		Init(n);
		for (int i = 1; i <= n; ++i)
			read(a[i]);
		for (int i = 1; i < n; ++i) {
			read(x), read(y);
			add(x, y), add(y, x);
		}
		DFS1(1, -1);
		f[1] = s[1];
		DFS2(1, -1, 0);
		print(res, '\n');
	}
	return 0;
}
} // namespace XSC062
#undef int

E. 连珠线

http://222.180.160.110:1024/contest/3744/problem/5

哇塞，这个题有意思哇。

第一个 trick，蓝线成对出现。

第二个 trick，蓝线的连接有如下两种方式：

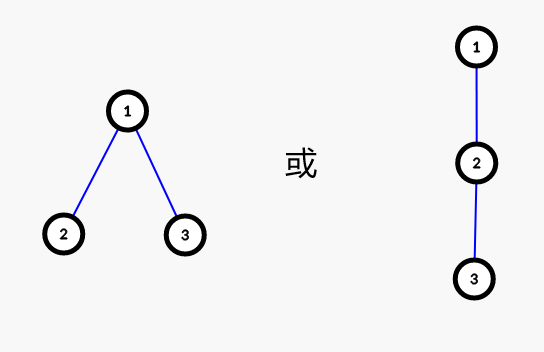
第三个 trick，从样例一可以看出，第一种连接方式中的根节点只能同时作为一组蓝线的中间结点。

C. 概率充电器

http://222.180.160.110:1024/contest/3744/problem/3

posted @ 2023-07-06 20:36  XSC062  阅读(11)  评论(0)  编辑  收藏  举报