230602 做题记录 // 儿童节快乐

一共有七块钱，花了两块买了一个我叶的吧唧。

为什么只买一个呢？因为剩下的几个长得还没我自己画的好看，，，

还有两块钱买了一个灯，剩下三块钱加入崩门，还有一块钱充公了。

你说，2 + 2 + 3 + 1 不是等于 8 吗？你猜 ~

---

A. Strange Way to Express Integers

http://222.180.160.110:1024/contest/3656/problem/1

Click me XD

---

B. 滑动窗口

http://222.180.160.110:1024/contest/3656/problem/2

字面意思。。。

namespace XSC062 {
using namespace fastIO;
const int maxn = 1e6 + 5;
int n, k, h, t;
int a[maxn], q[maxn];
int main() {
	read(n), read(k);
	h = 1, t = 0;
	for (int i = 1; i <= n; ++i) {
		read(a[i]);
		if (h <= t && i - q[h] >= k)
			++h;
		while (h <= t && a[i] <= a[q[t]])
			--t;
		q[++t] = i;
		if (i >= k)
			print(a[q[h]], ' ');
	}
	putchar('\n');
	h = 1, t = 0;
	for (int i = 1; i <= n; ++i) {
		if (h <= t && i - q[h] >= k)
			++h;
		while (h <= t && a[i] >= a[q[t]])
			--t;
		q[++t] = i;
		if (i >= k)
			print(a[q[h]], ' ');
	}
	return 0;
}
} // namespace XSC062

---

C. 工作安排

http://222.180.160.110:1024/contest/3656/problem/3

妙妙贪心题，想了好久好久。

不难发现被选中的 $i$ 需要满足 $b_i \le S_a - a_i$。

然后下意识变形，得到 $a_i + b_i \le S_a$。

不难想到尝试枚举可能的 $S_a$ 的值，并判断是否存在 $k$ 个 $i$，使得 $\sum a_i = S_a$，且对于 $\forall \, i$，有 $a_i + b_i \le S_a$。

那光是枚举就会起飞，更何况还存在一个目测只能暴搜判定的 check。

这里有两个分化点：

1. 若 $\sum a_i \ge S_a$，且 $a_i + b_i \le S_a$，那么明显有 $a_i + b_i \le S_a$。

   这代表着什么呢？$S_a$ 对 $a_i$ 的要求从 $\sum a_i = S_a$ 下降为了 $\sum a_i \ge S_a$。

   那么 check 就会好判定很多了。

   题外话：智力没悟到这个 trick 哈哈哈，我给他讲了半天他都是懵的，后来幡然醒悟气得差点从七楼跳下去哈哈哈

2. 这个点有点抽象。不妨这么想：假设平面上有若干个起点相同的区间，区间 $i$ 的范围为 $[0, a_i + b_i]$，赋予其权值为 $a_i$。将这些区间按照长度从小到大排序。

   

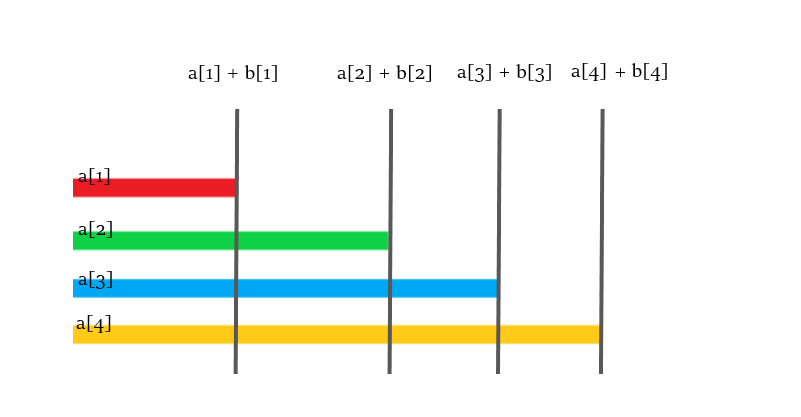
   那么待求就可以转化为，在数轴上寻找一个 $S_a$，满足存在 $k$ 个右端点在 $S_a$ 左边的区间，其权值和大于等于 $S_a$。

   一个很关键的 trick 就是，$S_a$ 一定会落在某个区间的右端点，即上图中的灰色分割线处。

   为什么呢？对于 $a_i + b_i$ 和 $a_{i + 1} + b_{i + 1}$ 中间的部分，即任意两根相邻分割线中间的空白部分，$S_a$ 落在上面是没有意义的。从 区间 $i$ 的右端点开始，一直到 区间 $i + 1$ 的右端点之前，右端点在 $S_a$ 前面的区间都只有前 $i$ 个，而当 $S_a$ 越小时，$\sum a_i \ge S_a$ 越容易满足，所以就选择可行范围内最小的 $a_i + b_i$。

那么思路就出来了。我们把给定的区间按 $a_i + b_i$ 从小到大排序，对于每一个 $i$，我们判定一下 $\sum _{j = 1}^i a_j$ 是否大于等于 $a_i + b_i$。

如果是，那么就会存在一组可行解，满足 $k = i$。因为 $i$ 越往后越大，我们只求最小的 $k$，所以输出第一个可行的 $i$ 即可…… 真的是这样吗？

在前 $i$ 个区间中，如果我们去除一个权值最小的区间，$\sum a \ge a_i + b_i$ 仍有可能成立，去除了第二小、第三小…… 也都有可能。

所以我们用一个小根堆存储所有权值，只要 $\sum a\ge a_i + b_i$，我们就不断弹出队头。

还没完。因为现在 $k$ 不一定等于 $i$ 了，所以得到的第一个可行解不一定就是最优解。所以我们要把所有 $a_i + b_i$ 作为 $S_a$ 的情况都过一遍。

那就又迎来了一个问题，假如我们在 $i=i_1$ 时从优先队列中弹出了一些元素，但在 $i=i_2 \ge i_1$ 时不想弹出这些元素，怎么办呢？

也就是说，对于 $p\le i_1, i_1\le q\le i_2$，存在 $a_p \ge a_q$，且 $a_p$ 已被弹出。下证这种情况不可能成为最优解。

对于 $i = i_1$，假设答案为 $k_1$，那么这 $k_1$ 个区间权值一定都大于等于 $a_p$。既然要恢复 $a_p$，那么不可能抛弃权值更大的原先 $k_1$ 个区间。即使抛弃了在 $i_1$ 之后的所有区间，答案也是会比 $k_1$ 大的。

题外话：这个 trick 我在 A 了过后写博客的时候才发现……

时间复杂度 $\mathcal O(n \log n)$，其中 $\log$ 是排序。

#define int long long
namespace XSC062 {
using namespace fastIO;
const int inf = 1e18;
const int maxn = 5e5 + 5;
struct _ { int a, b; };
_ a[maxn];
int n, s, cnt, res = inf;
std::priority_queue<int, std::vector<int>,
                            std::greater<int> > q;
inline int min(int x, int y) {
	return x < y ? x : y;
}
int main() {
    read(n);
    for (int i = 1; i <= n; ++i) {
        read(a[i].a), read(a[i].b);
        a[i].b += a[i].a;
	}
    std::sort(a + 1, a + n + 1,
        [&](_ x, _ y) { return x.b < y.b; } );
    for (int i = 1; i <= n; ++i) {
        s += a[i].a;
        q.push(a[i].a);
        if (s >= a[i].b) {
            while (q.size() && s - q.top() >= a[i].b)
                s -= q.top(), q.pop(), ++cnt;
            res = min(res, i - cnt);
        }
    }
    if (res == inf)
    	puts("-1");
    else print(res);
    return 0;
}
} // namespace XSC062
#undef int