230207

A. 整除分块

http://222.180.160.110:1024/contest/3160/problem/1

首先看到题面，不难想到暴力：

枚举 \(i=1\sim n\)，对每个 \(i\) 再枚举因数 \(1\sim i\)，判断是否整除，计算因数个数。

值得注意的是，\(n\le 10^{12}\)。

很自然地联想到一道小奥题：求 \(n!\) 的末尾有多少个 \(0\)，相当于询问 \(n!\) 的质因数分解中有多少个 \(5\)。我们的处理方式是，计算 \(\lfloor n\div 5\rfloor\) 得到 \(1\sim n\) 中 \(5\) 的倍数的个数，再计算 \(\lfloor n\div 25 \rfloor\) 得到 \(1\sim n\) 中 \(25\) 的倍数的个数，以此类推。

我不知道我为什么要用这个意义不明的例子来引入，但我确实在想到这个处理方式时就知道了这道题的解法（乐）

原问题可转化为 \(\sum\limits_{i=1}^n\sum\limits_{j=1}^i[j\mid i]\)，变形得到 \(\sum\limits_{j=1}^n\sum\limits_{i=1}^n[j\mid i]\)。其中的 \(\sum \limits_{i=1}^n[j\mid i]\) 就可以用上面的小奥方法来解决了，其答案就是 \(\left \lfloor \dfrac nj \right \rfloor\)。原问题转化为 \(\sum_{i=1}^n\left\lfloor\dfrac ni\right\rfloor\)。

这时候可以采用整除分块 / 数论分块来解决问题。

假设 \(n = 11\)，我们作出 \(y=\dfrac {11}x\) 的函数图像，并描出对于每一个 \(x\)，函数下方的第一个整点，即 \((x,\left\lfloor\dfrac {11}i\right\rfloor)\)，观察其 \(y\) 坐标。

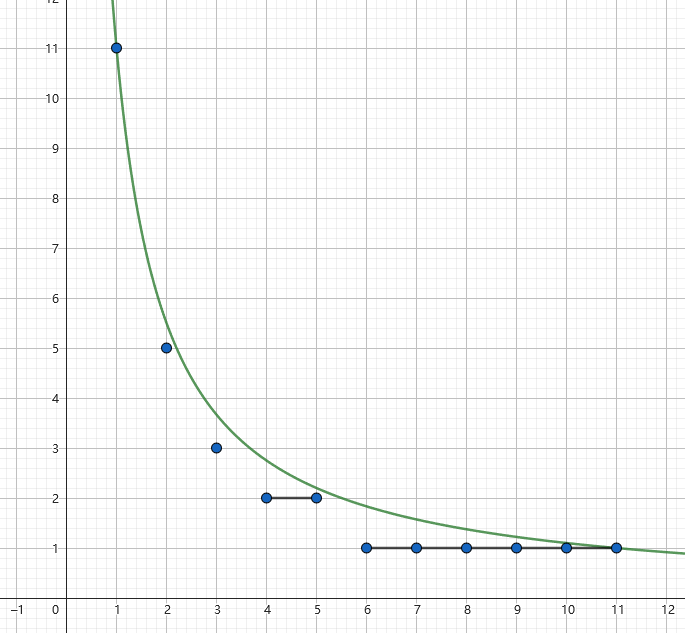
回到原问题。我们要求 \(\sum_{i=1}^n\left\lfloor\dfrac ni\right\rfloor\)，又已知在每连续的一段数中，\(\left\lfloor\dfrac ni\right\rfloor\) 相等，不难想到，对于每一个 \(\left\lfloor\dfrac ni\right\rfloor\)，计算其出现的次数。

upd on 240126。

问题等同于计算上图中满足同一段 \(y\) 坐标相同的点中，最右端的点的 \(x\) 坐标。即对于 \(\left\lfloor \dfrac ni \right\rfloor\)，需寻找 \(k_{\max}\)，满足 \(\left\lfloor \dfrac ni \right\rfloor=\left\lfloor \dfrac nk \right\rfloor\)，易知 \(k=\left\lfloor \dfrac n{\left \lfloor \frac ni\right \rfloor}\right\rfloor\)。

整除分块的思想，大概就是把同一 \(y\) 值对应的连续一段 \(x\) 划作一块。

回到上方的图像，我们发现这个函数图像呈反比例下降趋势（这个词是我自己发明的，敬爱的金山 KING 我对不起您），大胆猜测连续段会越来越长。

于是乎我们对于每一个 \(i\)，计算 \(\left\lfloor \dfrac ni \right\rfloor\) 后，乘上块长，add to 答案后直接跳到下一块第一个位置，本问题就得到了解决。

接下来我们要证明复杂度。我们发现复杂度只和块数有关。有引理：

\[\forall \, n\in \N_+,\left|\left\{\left \lfloor\dfrac{n}{d}\right\rfloor\mid d\in\N_+,d\le n\right\}\right|\le 2\sqrt n \]

其中 \(|S|\) 代表集合 \(S\) 的大小。

对于 \(d\le \sqrt n\)，\(\left\lfloor\dfrac nd\right\rfloor\) 取值不超过 \(\sqrt n\) 即 \(d\) 的取值数量。

其实此处应该取等，从函数图像可以看出。但鉴于我是数学等级为 C（过去完成时）的优秀高一生，我表示没听说过求导。所以我们只能用图像这种低劣的手段进行解释。
对于 \(d>\sqrt n\)，则 \(\left\lfloor\dfrac nd\right\rfloor\le \sqrt n\)，最多 \(\sqrt n\) 种取值。

综上，最多 \(2\sqrt n\) 种取值。

故时间复杂度 \(2\sqrt n\)。

#define int long long
namespace XSC062 {
using namespace fastIO;
int T, n, res;
int main() {
	read(T);
	while (T--) {
		read(n), res = 0;
		for (int i = 1; i <= n; ++i) {
			int r = n / (n / i);
			res += (r - i + 1) * (n / i);
			i = r;
		}
		print(res, '\n');
	}
	return 0;
}
} // namespace XSC062
#undef int

C. K 匿名序列

http://222.180.160.110:1024/contest/3160/problem/3

考虑题目给定的条件：递增、操作只有减。

不难发现，对于某个数 \(i\)，我们只能将其变为前面的某个数。

为了斜优，我们盲猜一个结论：若 \(a_i\) 需要变为前面的 \(a_j\)，那么 \(a_{j\sim i}\) 都需要变成 \(a_j\)。

这个猜想很好证明。若 \(a_i\) 要变成 \(a_j\)，但 \(a_k(j\le k\le i)\) 要变成 \(a_l(l<j)\)：

假如与 \(a_l\) 相等的数已经有 \(k\) 个，那么就不需要 \(a_k\) 的贡献了，\(a_k\) 为什么不减成代价更小的 \(a_j\) 呢？
否则，可以直接让 \(a_j\) 变成 \(a_l\)，而 \(a_{j+1\sim i}\) 可以变成 \(a_{j+1}\)，此时 \(a_{j+1\sim i}\) 的代价全部减小，\(a_j\) 变成 \(a_l\) 的代价又一定小于 \(a_k\) 变成 \(a_l\) 的代价，何乐而不为呢？

所以我们证明了这个猜想。接下来列出 DP 式：

\[f_i=\min\{f_{j}+(s_i-s_j)-a_{j+1}\times(i-j)\} \]

设 \(j>k\)，若满足：

\[\dfrac {(f_j-s_j+j\times a_{j+1})-(f_k-s_k+k\times a_{k+1})}{a_j-a_k}< i \]

则 \(j\) 优于 \(k\)。于是乎大胆斜优。

namespace XSC062 {
using namespace fastIO;
const int maxn = 5e5 + 5;
int T, n, k, h, t;
int a[maxn], s[maxn], f[maxn], q[maxn];
inline int getup(int j, int k) {
    return (f[j] - s[j] + j * a[j + 1])
            - (f[k] - s[k] + k * a[k + 1]);
}
inline int getdown(int j, int k) {
    return a[j + 1] - a[k + 1];
}
inline int getdp(int i, int j) {
    return f[j] + (s[i] - s[j]) - a[j + 1] * (i - j);
}
int main() {
    read(T);
    while (T--) {
        read(n), read(k);
        q[h = t = 1] = 0;
        for (int i = 1; i <= n; ++i) {
            read(a[i]), s[i] = s[i - 1] + a[i];
            while (h < t && getup(q[h + 1], q[h])
                    <= i * getdown(q[h + 1], q[h]))
                ++h;
            f[i] = getdp(i, q[h]);
            if (i + 1 < 2 * k)
                continue;
            int p = i - k + 1;
            while (h < t && getup(p, q[t])
                        * getdown(q[t], q[t - 1])
                        <= getup(q[t], q[t - 1])
                        * getdown(p, q[t]))
                --t;
            q[++t] = p;
        }
        print(f[n], '\n');
    }
    return 0;
}
} // namespace XSC062

E. 不祥之刃

http://222.180.160.110:1024/contest/3287/problem/2

本来以为，我们针对每一个 p，对其前方在前一个 p 之后的所有数从大到小排序，从前往后扫就可以了，后来被这组手造数据 Hack 了：

前四个被选取数本来应该是 { 20, 19, 14, 12 }，但是却按顺序选取了 { 20, 14, 12, 5 }。所以这个方法假了。

那换一个思路。不妨使用大根堆维护。碰到一个 d 时，将其加入优先队列，并记录其下标（用于限制选取个数），最后把整个优先队列过一遍就行了。

具体过的方式：过到 \(i\) 时，寻找其下一个 p（为保障复杂度需预处理，记为 \(j\)），用树状数组记录 \(1\sim j\) 共选取了多少个数，判断其加上一是否大于等于 \(j\) 的权值，如果否，则选取 \(i\)，并在 \(i\) 处加一。

然后很快被这组数据 Hack 得体无完肤：

12 1
d 3
p 3
d 4
p 8
d 17
d 1
d 14
d 11
d 16
p 6
d 3
d 14

程序将选择第一个 d 1，但不会计数到后面的 d 6 上。

好的，那我们针对这个情况解决问题。将大根堆改为小根堆，以此维护前权值大个数。好了，然后就可以了，rnm。

namespace XSC062 {
using namespace fastIO;
const int inf = 1e18;
const int maxn = 5e5 + 5;
char op;
int a[maxn];
bool flag[maxn];
int n, m, la, res, cnt;
std::priority_queue<int, std::vector<int>,
                        std::greater<int> > q;
inline int min(int x, int y) {
    return x < y ? x : y;
}
int main() {
    read(n), read(m);
    for (int i = 1; i <= n; ++i) {
        scanf("%1s", &op);
        read(a[i]);
        if (op == 'p') 
            flag[i] = 1;
    }
    a[la = n + 1] = inf;
    for (int i = n; i; --i) {
        if (!flag[i])
            continue;
        a[i] = min(a[i], a[la]);
        la = i;
    }
    for (int i = 1; i <= n; ++i) {
        if (flag[i]) {
            while ((int)q.size() >= a[i])
                q.pop();
        }
        else q.push(a[i]);
    }
    cnt = q.size();
    while (!q.empty()) {
        res += q.top();
        q.pop();
    }
    if (cnt >= m)
        print(res);
    else puts("-1");
    return 0;
}
} // namespace XSC062

F. 防线

http://222.180.160.110:1024/contest/3287/problem/4

我看不懂啊，这为啥是二分啊？

看了一眼 IDSY 三年前的博客（害怕），才发现，woc，这谁想得到前缀和啊。

感觉不对劲，又看了一眼，woc，这谁想得到直接求和模拟前缀和啊。

观察整个 \(1\sim 2^{31}-1\) 序列上的值。若某个值为奇数，则其他数都是偶数。我们想到了什么，奇偶性分析。奇数与无数个偶数的和一定是奇数，所以我们想到了前缀和。自某个奇数值元素开始，往后的所有前缀和都是奇数，而往前的都是偶数。

所以这是什么，这是二分，我们二分奇数前缀和出现的位置即可。

但是值域是 \(2^{31}\)，像个鸡毛一样，所以我们想到每次求解 [1, mid] 之间的防具数量之和，具体方法：枚举每个给定的等差数列，计算其在 [1, mid] 范围内的项数。

时间复杂度 \(\mathcal O(31\times n)\)。

namespace XSC062 {
using namespace fastIO;
const int maxn = 2e5 + 5;
struct _ {
    int l, r, d;
};
_ a[maxn];
int T, n, l, mid, r, res, cnt;
inline int min(int x, int y) {
    return x < y ? x : y;
}
inline bool check(int x) {
    int res = 0;
    for (int i = 1; i <= n; ++i) {
        if (x >= a[i].l) {
            res += (min(x, a[i].r) - a[i].l)
                                / a[i].d + 1;
        }
    }
    return (res & 1);
}
int main() {
    read(T);
    while (T--) {
        read(n);
        for (int i = 1; i <= n; ++i)
            read(a[i].l), read(a[i].r), read(a[i].d);
        l = 1, r = INT_MAX, res = -1;
        while (l <= r) {
            mid = (l + r) >> 1;
            if (check(mid))
                res = mid, r = mid - 1;
            else l = mid + 1;
        }
        if (res == -1)
            puts("There's no weakness.");
        else {
            print(res, ' ');
            cnt = 0;
            for (int i = 1; i <= n; ++i) {
                if (res >= a[i].l && res <= a[i].r
                        && !((res - a[i].l) % a[i].d))
                    ++cnt;
            }
            print(cnt, '\n');
        }
    }
    return 0;
}
} // namespace XSC062

btw，等差数列项数计算公式居然是末项减首项除以公差加一。涨知识了。

G. 幻想乡 Wi-Fi 搭建计划

http://222.180.160.110:1024/contest/3289/problem/6

不难想到把题目抽象成图论模型：

可它不可做啊。无边权都不可做啊。知道为什么吗？

缺少了「坐标」这一关键限制条件。

posted @ 2023-02-18 16:51 XSC062 阅读(24) 评论(0) 编辑收藏举报

刷新页面返回顶部

博客标题

博客子标题