马走日,就先这样吧(?)

题目描述

马在中国象棋以日字形规则移动。
请编写一段程序，给定 \(n*m\)大小的棋盘，以及马的初始位置\((x,y)\)，要求不能重复经过棋盘上的同一个点，计算马可以有多少途径遍历棋盘上的所有点。

输入格式

第一行为整数\(T(T < 10)\)，表示测试数据组数。 每一组测试数据包含一行，为四个整数，分别为棋盘的大小以及初始位置坐标\(n,m,x,y\)。\((0 \leq x\le n-1,0 \leq y \leq m-1, m < 10, n < 10)\)

输出格式

每组测试数据包含一行，为一个整数，表示马能遍历棋盘的途径总数，0为无法遍历一次。

样例

样例输入

1
5 4 0 0

样例输出

32

白话文翻译

有 \(T\) 组测试用例，每组有一 个\(n*m\)的棋盘，一匹马有以下几种走法↓:

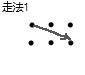
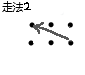
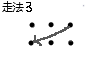
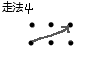
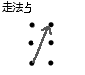
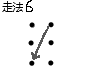
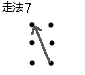
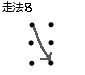
问这匹马能否不重复地走完棋盘上所有的点，如果能，输出方案总数。

思路

我都看得出来的 \(dfs\) ，你有什么理由看不出来?!（看是看出来了可惜还是做了半天我真蒻 ）

上代码

#include<cstdio>
#include<cstring>
const int fangx[10]={2,-2,-2,2,-1,1,-1,1};
const int fangy[10]={-1,1,-1,1,2,-2,-2,2};
bool vis[15][15];
int ans;
int t,n,m,cx,cy,nm;
void dfs(int x,int y,int stp){
	int nx,ny;
	if(stp==nm){			//stp为当前所走步数，如果和所需步数相等，说明已经遍历完毕
		ans++;
		return;
	}
	for(int i=0;i<8;++i){
		nx=x+fangx[i],ny=y+fangy[i];
		if(nx<=0||ny<=0||nx>n||ny>m)continue;
		if(!vis[nx][ny]){
			vis[nx][ny]=1;
			dfs(nx,ny,stp+1);
			vis[nx][ny]=0;
		}
	}
	return;
}
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d%d%d%d",&n,&m,&cx,&cy);
		nm=n*m;				//棋盘格点总数，也就是马一共要走的步数
		cx++,cy++;			//由于起点坐标从0开始，而这里从1开始，所以把起点坐标+1
		memset(vis,0,sizeof(vis));
		ans=0;
		vis[cx][cy]=1;
		dfs(cx,cy,1);
		printf("%d\n",ans);
	}
	return 0;
}

2020.10.27 Update

原来我的第一篇blog不管格式、内容、都那么垃圾吗。。。（用C语言头文件是什么奇怪的癖好）
还是那句话，小学六年级，见谅。（虽然写这篇的时候好像是五年级来着）

end.