组合数学-二项式系数
组合数学-二项式系数
1.帕斯卡公式
分两种情况：
- 在前 \(n-1\) 个中已经选出 \(m\) 个；
- 在前 \(n-1\) 个中选出 \(m-1\) 个，加上刚刚选的第 \(m\) 个。
可用于 \(O(n^2)\) 预处理组合数。
2.组合恒等式
i.吸收恒等式
- Proof：
同理可得：
ii.对称恒等式
组合意义：\(n\) 选 \(m\)，相当于 \(n\) 个中不选 \(n-m\) 个。
iii.上指标求和1
- Proof\[\begin{aligned}\sum_{i=0}^n \binom{m+i}{m} &= \binom{m}{m} +\binom{m+1}{m} + \dots + \binom{m+n}{m} \\&= \binom{m+1}{m+1} + \binom{m+1}{m} + \binom{m+2}{m} + \dots + \binom{m+n}{m}\\ &= \binom{m+2}{m+1} + \binom{m+2}{m} + \dots + \binom{m+n}{m} \\&= \binom{m+3}{m+1} + \binom{m+3}{m} + \dots + \binom{m+n}{m} \\&= \binom{m+n+1}{m+1}\end{aligned} \]
iv.上指标求和2
组合意义：考虑 \(n+1\) 个物品中选 \(k+1\) 个，若最后一个选出的物品是第 \(i\) 个，那么前面选择方案有 \(\binom{i-1}{k}\) 种。
v.对角线求和
利用对称恒等式转化为上指标求和 1。
vi.组合数前缀和
设 \(S_{n,m}=\sum_{i=0}^{m} \binom{n}{i}\)。有递推：
vii.范德蒙德卷积
从 \(A\) 集合选出 \(x\) 个，从 \(B\) 集合选出 \(y\) 个，当 \(x+y\) 为定值时可套用。
若 \(x-y\) 为定值，转化为在 \(B\) 集合中不选 \(m-y\) 个，那么 \(x+m-y\) 为定值，得到 \(\binom{n+m}{x+m-y}\)。
viii.格路计数
从 \((0,0)\) 向下、向右走到 \((n,m)\) 的方案数为 \(\binom{n+m}{n}\)。
组合意义：总共要走 \(n+m\) 格， \(n\) 格向下，\(n-m\) 格向右。在 \(n-m\) 步中选择 \(n\) 步向下走。
3.二项式定理
Theorem
组合意义：将原式全部拆开，对于 \(a^ib^{n-i}\) 项，在拆开后的式子中出现了 \(\binom{n}{i}\) 次。
代数推导：数学归纳法。当 \(n=1\) 时显然成立。当 \(n>1\) 时，假设 \(n-1\) 成立，则：
i.下指标求和1
组合意义：设 \(S={1,2,3,...,n}\)，\(S_i\) 为 \(S\) 大小为 \(i\) 的子集的集合。所有 $S_i $ 的并集是 \(S\)，且两两不交。
代数意义：二项式定理，\((1+1)^n\)。
ii.下指标交错和
代数意义：原式化为 \((1-1)^n\)。
组合意义：在 \(n\) 个物品中选择奇数个物品的方案等于选择偶数个物品的方案。假设我们要选取偶数个物品，前 \(n-1\) 个物品可以任选。如果已经选出了偶数个物品，那么第 \(n\) 个不选；如果已经选择了奇数个，那么第 \(n\) 个必须选，则总方案数为 \(2^{n-1}\)。要选取奇数个物品也是同理的，总方案数也是 \(2^{n-1}\)。
iii.下指标求和2
代数推导：
4.不定方程整数解问题
Problem A.
现有 \(k\) 个未知数 \(x_1,x_2,x_3,...x_k\)，求不定方程 正整数解 的个数：\(\sum x_i=n\)。
我们假设现在有 \(n\) 个物品排成一排，每两个物品中间都有一个空当，共有 $n-1 $ 个空当。
若要把这 \(n\) 个物品分成 \(k\) 部分，那么我们需要插入 \(k-1\) 个 “隔板”，共有 \(\binom{n-1}{k-1}\) 种方案。
对于每一种方案，我们就令 \(x_i\) 为分出的第 \(i\) 个部分中物品个数，可以唯一对应一种合法的解。
对于每一组解，我们令第 \(i\) 个部分中物品个数为 \(x_i\)，可以唯一对应一种插隔板的方案。
则解的个数就是插板方案数，即 \(\binom{n-1}{k-1}\)。
Problem B.
现有 \(k\) 个未知数 \(x_1,x_2,x_3,...x_k\)，求不定方程 非负整数解 的个数：\(\sum x_i=n\)。
令 \(y_i=x_i+1\)，那么 \(\sum y_i=n+k\).。此时 \(y_i\) 一定为正整数。
\(y_i\) 的合法解，能够与 \(x_i\) 的合法解一一对应。由上面的叙述，可知 $y_i $ 解的个数为 \(\binom{n+k-1}{k-1}\)，那么原问题的答案也是 \(\binom{n+k-1}{k-1}\)。
5.多重集合的排列与组合
首先引入多重集合的概念：
- 确定的、无序的、可重的集合。
由 \(1\) 个 \(x\)，\(3\) 个 \(y\)，\(5\) 个 \(z\) 组成的多重集合可表示为 \(\{ 1\cdot x,3 \cdot y,5\cdot z \}\)。
Problem A.
现有一个多重集合 \(S=\{c_1\cdot x_1,c_2\cdot x_2,...c_k\cdot x_k\}\)，\(\sum c_i=n\)。
我们任意地取出 \(S\) 的每一个元素排成一个序列，问会形成多少种不同的序列？
首先我们拿出 \(c_1\) 个 \(x_1\)，有 \(\binom{n}{c_1}\) 种安排位置的方案。
再拿出 \(c_2\) 个 \(x_2\)，有 \(\binom{n-c_1}{c_2}\) 种安排位置的方案。
依次进行下去，最后的答案即为：
展开二项式系数，进行约分即可。
Problem B.
现有一个多重集合 \(S=\{\infty\cdot x_1,\infty\cdot x_2,...\infty\cdot x_k\}\)。
我们任意地取出 \(S\) 的 \(m\) 个元素生成一个集合，问会形成多少种不同的集合？
问题转化为不定方程非负整数解问题：\(\sum x_i=m\) 的解个数。
答案就是 \(\binom{k+m-1}{k-1}\)。
6.二项式系数的单峰性
我们把 \(\binom{n}{0},\binom{n}{1},\binom{n}{2},\cdots,\binom{n}{n}\) 排成一个序列。那么存在一个 \(t\)，使得 \(1\sim t\) 不降，\(t\sim n\) 不升。
进一步地，若 \(n\) 为奇数，则 \(t=\lceil\dfrac{n}{2} \rceil\)，否则 \(t=\dfrac{n}{2}\) 或 \(\dfrac{n}{2}+1\)。
我们把 \(\binom{n}{k},\binom{n}{k-1}\) 拿出来作商，有：
若 \(n-k+1<k\)，则 \(k<\dfrac{n}{2}\)；
若 \(n-k+1=k\)，则 \(k=\dfrac{n}{2}\)；
若 \(n-k+1>k\)，则 \(k>\dfrac{n}{2}\)。
讨论一下 \(n\) 的奇偶即可。
7. 多项式系数
我们把二项式系数扩展到多项式系数：\(\binom{n}{c_1 \ c_2\ c_3 \cdots \ c_k}\) 表示把 \(n\) 个物品划分为 \(k\) 个集合，使得第 \(i\) 个集合大小为 \(c_i\) 的方案数。
我们有：
注意到它的值与 5.B 中多重集合排列问题的答案相等。
对于一种分割方案，我们考虑一个长度为 \(n\) 的序列 \(A\)，把所有第 \(i\) 个集合中的元素 \(x_j\) 拿出来，并令 \(A_{x_j}\) 等于 \(i\)。这样一种分割方案能够唯一对应一个多重集合的排列方案。
对于一种排列方案，我们把 \(A_i=j\) 的所有 \(i\) 全部放入 \(j\) 集合中，那么一种排列方案就唯一对应一种分割方案。
帕斯卡公式
组合意义：考虑第 \(n\) 个物品被分入了哪一个集合，加法原理即可。
代数推导：
多项式定理
我们把 \((x_1+x_2+\cdots+x_k)^n\) 展开。对于 \(x_1^{c_1}x_2^{c_2}\cdots x_k^{c_k}\) 这一项，会在展开的式子中出现 \(\binom{n}{c_1 \ c_2 \ c_3\ \cdots \ c_k}\) 次。
对展开后的式子合并同类项，最终不同的项会有 \(\binom{n+k-1}{k-1}\) 个（考虑转化为不定方程整数解问题）。
8.卢卡斯定理（Lucas）
Theorem
其中 \(p\) 为质数。
也就是把 \(n,m\) 表示为 \(p\) 进制数，对于每一位都分别求解再相乘。
适用于 \(n,m\) 都很大，但 \(p\) 较小时的情况。
Proof
-
引理：若 \(p\) 为质数，则 \((1+x)^p \equiv 1+x^p \pmod{p}\)。
Proof:
- 将 \((1+x)^p\) 利用二项式定理展开，得 \((1+x)^p = \sum\limits_{i=0}^p \binom{p}{i}x^i\)。
- 利用吸收恒等式变形： \(\sum\limits_{i=0}^p \binom{p}{i}x^i = 1+\sum\limits_{i=1}^p \dfrac{p}{i}\binom{p-1}{i-1}x^i\)。
- 对于 \(\forall i \in [1,p)\)，\(\dfrac{p}{i}\binom{p-1}{i-1} \mid p\)，则有 \((1+x)^p \equiv 1+x^p \pmod{p}\)。命题得证。
-
设 \(n=sp+q,m=tp+r\)。问题转化为证明 \(\binom{n}{m} \equiv \binom{s}{t} \times \binom{q}{r} \pmod{p}\)。
\(\binom{n}{m}\) 即为 \((1+x)^n\) 中 \(x^m\) 项的系数。
\[\begin{aligned}(1+x)^n &\equiv (1+x)^{sp+q} &\pmod{p}\\&\equiv (1+x)^{sp} \times (1+x)^q &\pmod{p}\\&\equiv [(1+x)^p]^s \times (1+x)^q &\pmod{p}\\&\equiv (1+x^p)^s \times (1+x)^q &\pmod{p}\\&\equiv (\sum\limits_{i=0}^s\binom{s}{i}x^{ip})(\sum\limits_{i=0}^q\binom{q}{i}x^i) &\pmod{p}\end{aligned} \]由于 \(x^m = x^{tp+r} = x^{tp}\times x^r\)，\(x ^ m\) 的系数也可表示为 \(\binom{s}{t} \times \binom{q}{r}\)。
则有 \(\binom{n}{m} \equiv \binom{\lfloor \frac{n}{p} \rfloor}{\lfloor \frac{m}{p} \rfloor} \times \binom{n \bmod p}{m \bmod p} \pmod{p}\)，命题得证。
利用 Lucas 定理，可以在 \(O(p)\) 处理阶乘数组与阶乘逆元数组后， \(O(\log_p n)\) 求出 \(\binom{n}{m} \bmod p\) 的值。
void Init(){
fac[0]=caf[0]=1;
for(int i=1;i<p;i++) fac[i]=fac[i-1]*i%p;
caf[p-1]=QuickPow(fac[p-1],p-2);
for(int i=p-2;i;i--) caf[i]=caf[i+1]*(i+1)%p;
}
ll C(int x,int y){
if(x<y) return 0;
return fac[x]*caf[y]%p*caf[x-y]%p;
}
ll Lucas(int x,int y){
if(x<p&&y<p) return C(x,y);
else return Lucas(x/p,y/p)*C(x%p,y%p)%p;
}
9.阶乘的素数幂次
设 \(p \in \mathbb{Prime}\)，则有：
其中 \(v_p(x)\) 表示 \(x\) 中包含 \(p\) 的次数。
将 \(1\sim n\) 分开，\(v_p(n!)=\sum_{i=1}^n v_p(i)\)。
\(1\sim n\) 中至少包含一个 \(p\) 的数字有 \(\lfloor \dfrac{n}{p} \rfloor\)，统计进答案中。\(1 \sim n\) 中至少包含 \(2\) 个 \(p\) 的数字有 \(\lfloor \dfrac{n}{p^2} \rfloor\) 个，但由于已经有一个 \(p\) 被统计过一遍，所以只需要再统计第 \(2\) 个质因子，答案加上 \(\lfloor\dfrac{n}{p^2}\rfloor\)，系数为 \(1\)。
我们从另一个角度来计算。用 \(p\) 进制表示 \(n\)，则有 \(n=\sum a_ip^i(0\leq a_i<p)\)。
其中 \(s_p(n)\) 表示 \(n\) 在 \(p\) 进制下各数位的数字之和。
10.Kummer 定理
在 \(p\) 进制下 \(n-m\) 与 \(m\) 相加，结果为 \(n\)。
设进位次数为 \(c\)。每进位一次，数位之和就会减少 \(p-1\)，那么有
于是得到 \(\binom{n}{m}\) 中 \(p\) 的次数，就是 \(n-m\) 与 \(m\) 在 \(p\) 进制下相加进位次数。
同理可得， \(\binom{n}{m}\) 中 \(p\) 的次数就是 $n $ 与 \(m\) 在 \(p\) 进制下相减的借位次数。
若 \(\binom{n}{m}\) 在模 \(p\) 意义下为 \(0\)，那么 \(n,m\) 在 \(p\) 进制下相减时至少产生了一次借位。
换句话说，如果在 \(p\) 进制下存在一位，使得 \(n\) 在这一位的值小于 \(m\) 在这一位的值，那么 \(\binom{n}{m} \bmod p\) 一定为 \(0\)。
由此可以快速判断 \(\binom{n}{m}\) 的奇偶性：设 \(n,m\) 在二进制下表示的集合为 \(S_n,S_m\)，\(\binom{n}{m}\) 为奇数当且仅当 \(S_m \subseteq S_n\)，也就是 \(n \operatorname{and} m = m\)。
11.卡特兰数
对于一个长度为 \(2n\) 的 01 序列 \(A\)，含有 \(n\) 个 \(0\) 和 \(n\) 个 \(1\)，满足对于任意的 \(i \in [1,2n]\)，\(A[1\sim i]\) 中 \(1\) 的个数不超过 \(0\) 的个数。
这样的 \(A\) 的个数，我们记为 \(Cat_n\)，也就是卡特兰数的第 \(n\) 项。
求法 1
欲求出 \(Cat_n\) 的值，不妨利用容斥，用总方案数 \(\binom{2n}{n}\) 减去不合法的方案数。
对于一个不合法的数列 \(B\)，存在一个位置 \(2p+1\)，满足 \(B[1\sim i]\) 中 \(0,1\) 分别出现了 \(p,p+1\) 次。那么 \(B[2p+2\sim 2n]\) 中 \(0,1\) 分别出现了 \(n-p,n-p-1\) 次。
反转 \(B[2p+2\sim 2n]\) 的每个元素，\(0\) 变 \(1\)，\(1\) 变 \(0\)。那么我们得到了一个含有 \(n+1\) 个 \(1\)，\(n-1\) 个 \(0\) 的数列。
对于一个含有 \(n+1\) 个 \(1\)，\(n-1\) 个 \(0\) 的数列 \(C\)，也存在一个这样的 \(2p+1\)。反转 \(C[2p+2\sim 2n]\)，又得到了一个含有 \(n\) 个 \(0\) 和 \(n\) 个 \(1\) 的数列。
每一个 \(B\) 都能得到一个唯一的 \(C\)，反过来亦然。那么不合法的方案数就是 \(C\) 的个数，即 \(\binom{2n}{n+1}\)。
于是我们得到：
求法 2
\(Cat_n\) 也可以表述为：在平面直角坐标系中，每次允许向 \(x\) 或 \(y\) 的正方向移动一格，从 \((0,0)\) 不超过 \(y=x\) 这条直线走到 \((n,n)\) 的方案数。
那么如果我们移动过程中触碰到了 \(y=x+1\) 这条直线，必定不合法。
考虑类似于 "反射" 的转化：如果触碰到了 \(y=x+1\)，那么移动 \(x\) 变为移动 \(y\)，移动 \(y\) 变为移动 \(x\)。最终我们会到达 \((n,n)\) 关于 \(y=x+1\) 的对称点 \((n-1,n+1)\)。
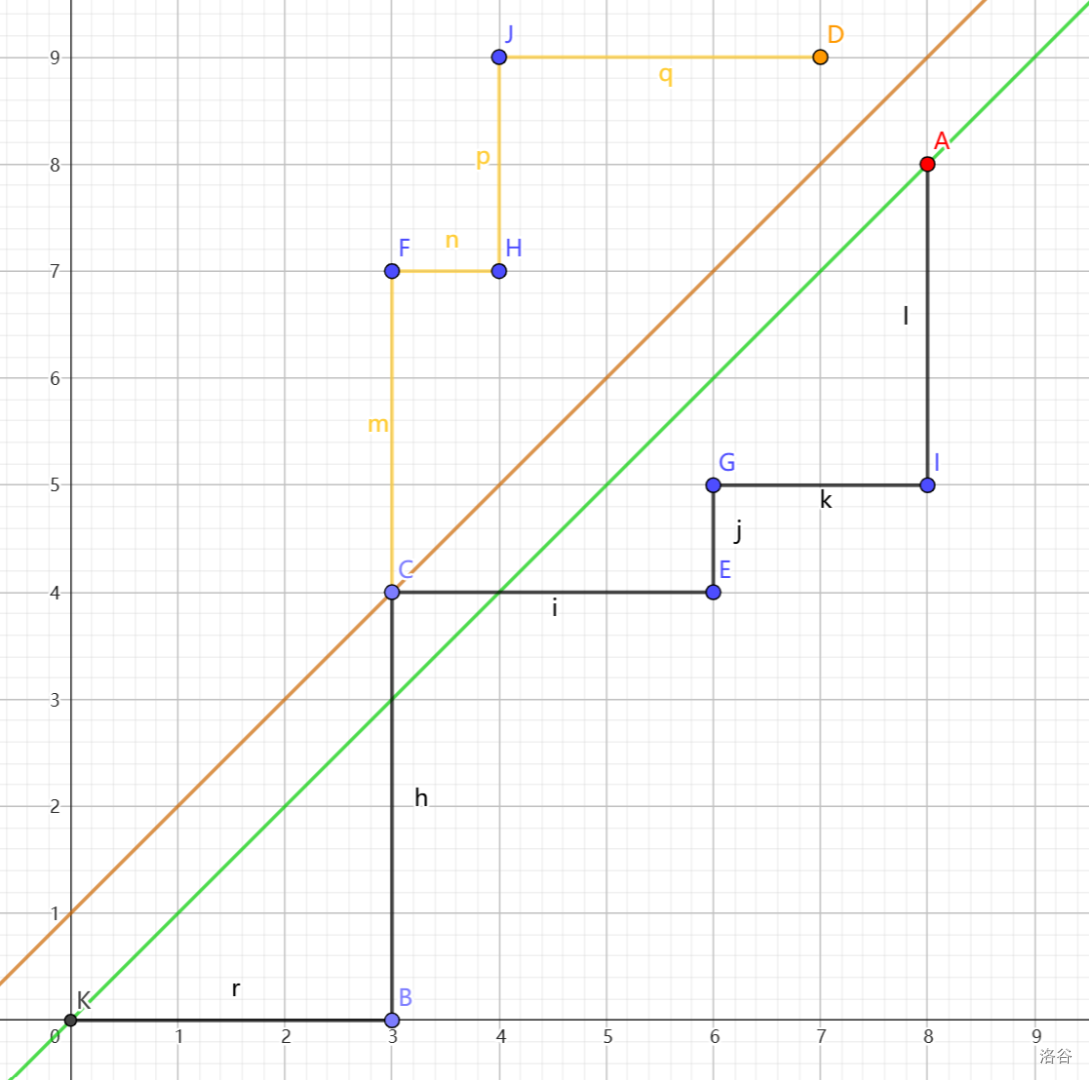
图中黑色折线为原路径，黄色折线为 “反射” 得到的直线。
那么不合法的走法有 \(\binom{2n}{n+1}\) 种，也可以得到与求法 1 相同的表达式。
卡特兰数的应用
- 长度为 \(2n\) 的括号序列个数为 \(Cat_n\)；
- \(n\) 个元素按顺序进栈，出栈序列的个数为 \(Cat_n\)；
- \(n\) 个节点能够构造出 $Cat_n $ 种不同的二叉树。
- ...
卡特兰数还有递推形式：
卡特兰数的前 \(10\) 项 （从 \(0\) 开始）：
