CF126B
朴素解法:求出原字符串的最长 border,并 kmp 匹配出出现在中间的最长 border,若没有则不断缩短 border 的长度,直到中间存在。若 border 长度减到了 \(0\),则无解。
我们通过画图来探索优化方式。

如图,蓝色部分为原串的最长 border,红色部分为蓝色部分的最长 border。
容易发现,红色部分就是我们要求的答案。
然后就做完了。具体实现细节见代码。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
string str;
int nxt[N],nxt2[N];
void getnxt(string t){
int i=0,j=-1;
nxt[0]=-1;
for(;i<t.size();){
if(j==-1||t[i]==t[j])
i++,j++,nxt[i]=j;
else
j=nxt[j];
}
}
int kmp(string s,string t){
getnxt(t); //注意还得求一遍 nxt
int i=0,j=0;
for(;i<s.size();){
if(j==t.size()-1&&s[i]==t[j])
return i-j+1; //直接 return 是为了找中间出现的,最后 return 会找到后缀
if(j==-1||s[i]==t[j])
i++,j++;
else
j=nxt[j];
}
return 0;
}
int main(){
ios::sync_with_stdio(0);
cin>>str;
getnxt(str);
int last=str.size()-nxt[str.size()];
string t=str.substr(last); //后缀(即最长 border)
memcpy(nxt2,nxt,sizeof nxt2);
int pos=kmp(str.substr(1),t); //str.substr(1) 是为了不取到前缀
if(pos<last){
if(t=="") cout<<"Just a legend",exit(0);
cout<<t,exit(0);
}
pos=nxt2[nxt2[str.size()]];
if((!pos)||(!nxt2[str.size()]))
cout<<"Just a legend",exit(0);
t=str.substr(0,pos);
cout<<t;
return 0;
}
P4824
朴素解法:每次 kmp 匹配出 \(T\) 的出现位置并删除直到 \(S\) 中不含有 \(T\) 即可。
我们通过发掘性质来探索优化方式。
观察这样一组数据:
momomoooo
moo
我们的操作方式是:
" momo 'moo' oo " -> " mo 'moo' o " -> " 'moo' " -> ""
可以发现,起始位置越靠后的子串,越先被消除,考虑使用栈进行维护。
具体的,我们记录 \(match_i\) 表示 \(S\) 中的每一个 \(i\),它要跳到的 \(T\) 中的下一个位置,这显然可以在 kmp 匹配的过程中维护。
同时,我们也用栈维护当前的 \(S\) 串。
每当一个 \(T\) 匹配成功后,栈弹出 \(\left| T \right|\) 个字符,并令 \(j\) 跳到此时栈顶所对应的 \(match\)。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e7+5;
string str1,str2;
int top,nxt[N],stk[N],match[N];
void getnxt(string t){
int i=0,j=-1;
nxt[0]=-1;
for(;i<t.size();){
if(j==-1||t[i]==t[j])
i++,j++,nxt[i]=j;
else
j=nxt[j];
}
}
int kmp(string s,string t){
getnxt(t);
int i=0,j=0;
for(;i<s.size();){
if(j==-1||s[i]==t[j])
match[i]=j+1,stk[++top]=i,i++,j++;
else
j=nxt[j];
if(j==t.size())
top-=t.size(),j=match[stk[top]];
}
}
int main(){
ios::sync_with_stdio(0);
cin>>str1>>str2;
kmp(str1,str2);
for(int i=1;i<=top;i++)
cout<<str1[stk[i]];
return 0;
}
P3435
首先,画图并发掘性质。
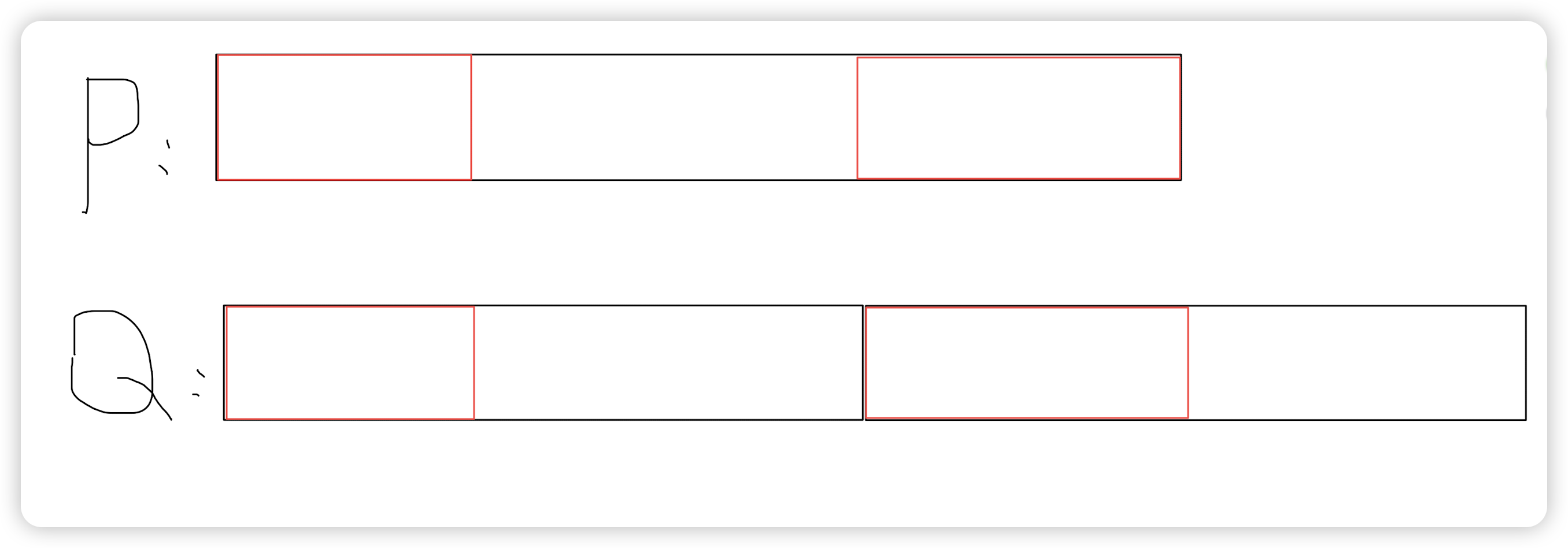
如图,\(Q\) 串是 \(P\) 串的一个周期。
显然 \(Q=P-红色部分\),而要使得 \(Q\) 最长,则红色部分一定最短。结合图分析,可将题目转化为求 \(P\) 的最短 border。
如何求最短 border?接下来我们专门研究 \(P\) 串。

如图,我不停地求出 \(P\) 串的 最长 border 的最长 border 的最长 border ...... 如此循环往复,容易发现最长 border 总是成对出现,且一定会有两个分别在 \(P\) 串的一头一尾。这样便一定能求出 \(P\) 的最短 border。
但是一步一步跳太慢了,我们加个记忆化即可。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e7+5;
int n,nxt[N];
string str;
void getnxt(string t){
int i=0,j=-1;
nxt[0]=-1;
for(;i<t.size();){
if(j==-1||t[i]==t[j])
i++,j++,nxt[i]=j;
else
j=nxt[j];
}
}
signed main(){
ios::sync_with_stdio(0);
cin>>n>>str;
int ans=0;
getnxt(str);
for(int i=2,j=2;i<=n;i++){
j=i;
while(nxt[j])
j=nxt[j];
if(nxt[i]!=0)
nxt[i]=j; //记忆化
ans+=i-j;
}
cout<<ans;
return 0;
}
CF494B
参考了 RainFestival 的题解。/bx/bx/bx
求方案数却不求具体方案,考虑 dp。
令 \(dp_i\) 表示分割方案的最后一个子串以 \(s_i\) 结尾的方案数(结尾定义状态)。
初始:\(dp_0=1\)(一个字符也有一种方案)。
转移:
\([x]\) 表示在条件 \(x\) 满足的情况下。
\(s \in t\) 表示 \(s\) 为 \(t\) 的子串。
\(i\) 满足 \(i \in [1,n]\)。
朴素转移是 \(O(n^3)\) 的(需要预处理 \([t \in s_{j \sim i}]\))。
容易发现,若在每个 \(i\) 之前找到一个最大的 \(y\) 使得 \(y+\left|t\right|-1 \le i\) 且 \(t \in s_{y \sim y+\left|t\right|-1}\),则所有满足 \(j \le y\) 的 \(j\) 才会满足 \(t \in s_{j \sim i}\)。其中 \(y\) 可以使用 kmp 求出。
于是转移变为:
还是 \(O(n^3)\),但快了一点。
考虑将式子变形。
(将掌管求和下标的求和符号提到里面来,方便化简)
(化简求和符号)
令:
则:
初始:
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e5+5;
const int MOD=1e9+7;
string s,t;
int d[N],tag[N],nxt[N];
int dp[N],ff[N],ss[N];
void getnxt(string y){
int i=0,j=-1;
nxt[0]=-1;
for(;i<y.size();){
if(j==-1||y[i]==y[j])
i++,j++,nxt[i]=j;
else
j=nxt[j];
}
}
void kmp(string x,string y){
getnxt(y);
int i=0,j=0;
for(;i<x.size();){
if(j==-1||x[i]==y[j])
i++,j++;
else
j=nxt[j];
if(j==y.size())
tag[i]=1,j=nxt[j];
}
}
signed main(){
ios::sync_with_stdio(0);
cin>>s>>t;
kmp(s,t);
d[0]=0;
for(int i=1;i<=s.size();i++)
d[i]=(tag[i]?i-t.size()+1:d[i-1]);
dp[0]=1,ff[0]=1,ss[0]=0;
for(int i=1;i<=s.size();i++){
if(!d[i]) dp[i]=0;
else dp[i]=((ff[d[i]-1]*d[i]%MOD-ss[d[i]-1])%MOD+MOD)%MOD;
ff[i]=(ff[i-1]+dp[i])%MOD;
ss[i]=(ss[i-1]+dp[i]*i%MOD)%MOD;
}
cout<<((ff[s.size()]-1)%MOD+MOD)%MOD; //这里减一是因为 ff 和 dp 的初始值都是一,转移时会重复加
return 0;
}




