Kobe-Morris-Pratt 算法
定义
一些基本定义:
- border:是一个字符串的子串(不与其本身相同)且满足既是其前缀又是其后缀的字符串,我们称之为该字符串的一个 border。
Kobe-Morris-Pratt 算法(以下简称 KMP 算法),是解决字符串匹配问题的一种算法,实际做题中常偏思维,通常用到的只有其中的 border 相关性质(即通常所说的 \(nxt\) 数组)。
在字符串匹配中,我们通常将被匹配的串称为文本串 \(s\),将与文本串匹配的串称为模式串 \(t\),下文亦同,且我们令 \(\left| s \right|\) 表示字符串 \(s\) 的长度,同时 \(\left| s \right| =n, \left| t \right|=m\)。
在字符串匹配中,当 \(s\) 与 \(t\) 某一下标的字符不相同,则我们称此种情况为 失配,下文亦同。
朴素匹配
显然,朴素匹配即为每次失配则令 \(t\) 移动一位继续尝试匹配直到全匹配上为止。
时间复杂度 \(O(n \times m)\)。
KMP 匹配
我们观察到,朴素匹配之所以效率低,是因为它每次失配时只让 \(t\) 移动一位。而失配时可能前面已经匹配了许多位,只移动一位就会导致大量的相同字符重复匹配。
结论:KMP 在每次失配时,\(t\) 串下标应跳到从开头到失配前一位的子串的最长 border 的长度的下标处。
证明:
-
Q:为什么要跳到 border 的长度下标处?
A:画个图观察可得,这样跳就是为了使 \(s\) 与 \(t\) 的后缀与前缀对齐。
-
Q:为什么要让后缀与前缀对齐?取中间的不行吗?
A:因为这样跳的距离更远,效率更高。
-
Q:为什么要跳到最长 border 的长度下标处?
A:选最长的 border,就意味着在 \(s\) 的最长后缀之前,不会有任何子串与 \(t\) 最长前缀有匹配的可能,那肯定选择直接跳过。而选的更小,则会导致前面可能有匹配的可能,从而导致遗漏。
综上所述即为 KMP 算法的主要逻辑与原理。
时间复杂度 \(O(n+m)\)。
最长 border 的求取
我们令 \(nxt_i\) 表示 \(t\) 在下标 \(i\) 失配后要跳到的位置。
根据上述推论,它同时也表示 \(t\) 在下标 \(i-1\) 结尾的最长 border 的长度。
既然是求最长相同的前缀与后缀,那么我们也可以不断尝试将 \(t\) 进行自匹配,每次成功匹配就记录 \(nxt\) 值,失配也按上述处理即可。
时间复杂度 \(O(n+m)\)。
综上,KMP 算法的总时间复杂度即为 \(O(n+m)\)。
P3375
板子。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
string s,t;
int nxt[N];
void getnxt(){
int i=0,j=-1;
nxt[0]=-1;
for(;i<t.size();){
if(j==-1||t[i]==t[j])
i++,j++,nxt[i]=j;
else
j=nxt[j];
}
}
void kmp(){
getnxt();
int i=0,j=0;
for(;i<s.size();){
if(j==t.size()-1&&s[i]==t[j])
cout<<i-j+1<<'\n',j=nxt[j];
if(j==-1||s[i]==t[j])
i++,j++;
else
j=nxt[j];
}
}
int main(){
cin>>s>>t;
kmp();
for(int i=1;i<=t.size();i++) cout<<nxt[i]<<' ';
return 0;
}
P4391
结论:答案即为 \(n-nxt_n\)。(KMP 题中有很多结论题,被薄纱了 /kk)
证明:
- Case 1:字符串最长 border 无重叠部分。
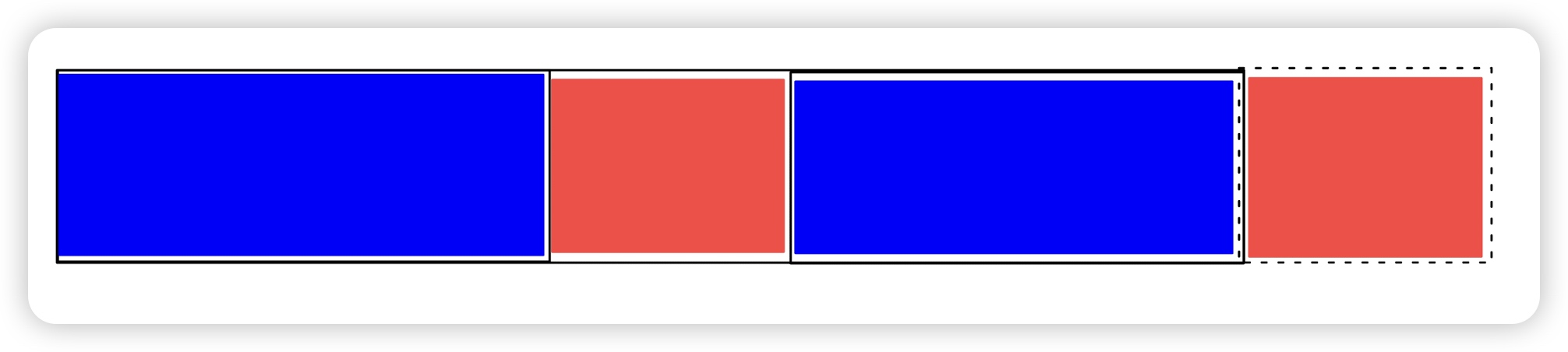
首先蓝色部分一定相等。
由于题目给的是子串,所以我可以复制一个红色部分使得两部分相等。
此时最短的为红 + 蓝,即 \(n-nxt_n\)。
还能更短吗?不能,因为空出来的部分没有子串可以复制出它。
- Case 2:字符串最长 border 有重叠部分。

(重叠部分为最中间的蓝色块)
首先,字符串内的蓝 + 红 + 蓝是一个最长 border,它们是相等的。
因为它们相等,蓝色部分又是后缀的一个前缀,所以我在前缀中也能找到一个相同的前缀,同理在后缀中也能找到一个相同后缀,复制一个红色部分后,后缀的相同后缀就能作为一个新的循环节的前缀了。
综上,最短的是蓝 + 红,即 \(n-nxt_n\)。
不能更短的原因同上。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
string s;
int n,nxt[N];
void getnxt(){
int i=0,j=-1;
nxt[0]=-1;
for(;i<n;){
if(j==-1||s[i]==s[j])
i++,j++,nxt[i]=j;
else
j=nxt[j];
}
}
int main(){
cin>>n>>s;
getnxt();
cout<<n-nxt[n];
return 0;
}
CF1200E
进食后人:不要用 substr / +,这俩玩意都是 \(O(n)\) 的,用 erase / += 替代即可。
容易观察到一个很显然的结论:将一个字符串接到之前答案的前面,记所拼成的新字符串的最长 border 的长度为 \(x\),则只要取前一个字符串加上后一个字符串去掉前 \(x\) 位即为当前答案。
然后直接做即可。
注意:
-
因为最长 border 长度不会超过两字符串长度取 \(\min\),于是只需取之前答案的这么多位即可,不然会超时;
-
拼接时要在中间加一个任意字符(不是大小写字母或数字),不然答案可能会越界。
code
#include<bits/stdc++.h>
using namespace std;
const int N=1e6+5;
int n,nxt[N];
string s[N];
int main(){
ios::sync_with_stdio(0);
cin>>n;
string ans="";
for(int i=1;i<=n;i++){
cin>>s[i];
if(i==1) ans+=s[i];
else{
string now="";
now+=s[i];
now+="#";
now+=ans.substr(ans.size()-min(ans.size(),s[i].size()));
int j=0,k=-1;
nxt[0]=-1;
for(;j<now.size();){
if(k==-1||now[j]==now[k])
j++,k++,nxt[j]=k;
else
k=nxt[k];
}
s[i].erase(0,nxt[now.size()]);
ans+=s[i];
}
}
cout<<ans;
return 0;
}




