众所周知,换根 dp 是非常套路的。换根真好玩(
换根 dp:
当不同节点作为根时,dp 结果不一致,若枚举每个节点作为根,则时间复杂度过高,在此种情形下,可使用 换根 dp 处理相邻两节点间的贡献,从而达到快速换根的效果。
使用场景:
对于一棵树,寻找以某节点 \(u\) 为根时取得的 最大值 / 最小值 / 方案数
实现步骤:
- 任选一节点作为根,跑一遍树形 dp,得到 \(dp_i\) 表示以 \(i\) 根的子树的 最大值 / 最小值 / 方案数。
- 令 \(f_i\) 表示以 \(i\) 为 全局根 时的 最大值 / 最小值 / 方案数,初始 \(f_1=dp_1\)。
- 从根再次 dfs,自父节点向子节点转移 \(f_i\)。
P3478
令 \(dp_i\) 表示以 \(i\) 为根的子树的节点全局深度之和。
(令 \(dp_i\) 表示为全局 / 局部信息依题而定,哪个方便做选哪个)
初始:\(dp_{cur}=dep_{cur}\)。
转移:\(dp_{cur}=dp_{cur}+dp_i\)(\(cur\) 为 \(i\) 的父节点)。
令 \(f_i\) 表示以 \(i\) 为全局根的节点深度之和。
初始:\(f_1=dp_1\)。
答案:\(\max\{f_i\}\)。
转移:
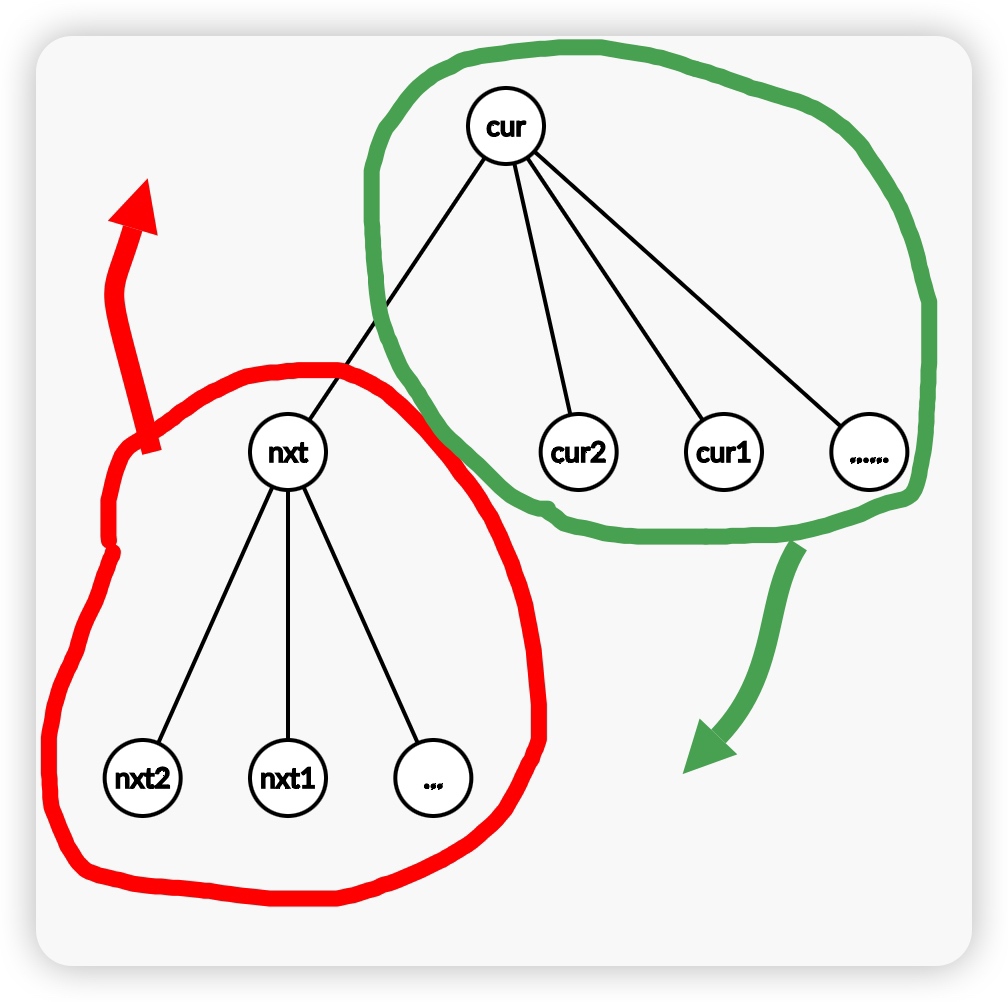
如图,以 \(nxt\) 为根的子树往上升,其子树内所有点的深度会减 \(1\);而以 \(cur\) 为根的子树往下降,其子树内所有点的深度会加 \(1\)。
于是有转移:
(\(siz_{nxt}\) 表示以 \(nxt\) 为根的子树大小)。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5;
int n;
vector<int> G[N<<1];
int dp[N],f[N],siz[N],dep[N];
void dfs1(int cur,int fa){
siz[cur]=1;
dp[cur]=dep[cur];
for(int i:G[cur]){
if(i==fa) continue;
dfs1(i,cur);
dep[i]=dep[cur]+1;
siz[cur]+=siz[i];
dp[cur]+=dp[i];
}
}
void dfs2(int cur,int fa){
for(int i:G[cur]){
if(i==fa) continue;
f[i]=f[cur]+n-2*siz[i];
dfs2(i,cur);
}
}
signed main(){
cin>>n;
for(int i=1,u,v;i<n;i++)
cin>>u>>v,
G[u].push_back(v),
G[v].push_back(u);
dep[1]=1;
dfs1(1,0);
f[1]=dp[1];
dfs2(1,0);
int ans=0,p=0;
for(int i=1;i<=n;i++)
if(ans<f[i])
ans=f[i],p=i;
cout<<p;
return 0;
}
P2986
这题实质即为上题加个边权。
令 \(dp_i\) 表示以 \(i\) 为根的子树的节点到它的带权路径和(局部)。
初始:\(dp_{cur}=0\)。
转移:\(dp_{cur}=dp_cur+dp_i+siz_i \times w\)(\(cur\) 为 \(i\) 的父节点,\(w\) 表示边 \(cur \to i\) 的边权)。
令 \(f_i\) 表示以 \(i\) 为全局根的带权路径和的最小值。
初始:\(f_1=dp_1\)。
答案:\(\min\{f_i\}\)。
转移:
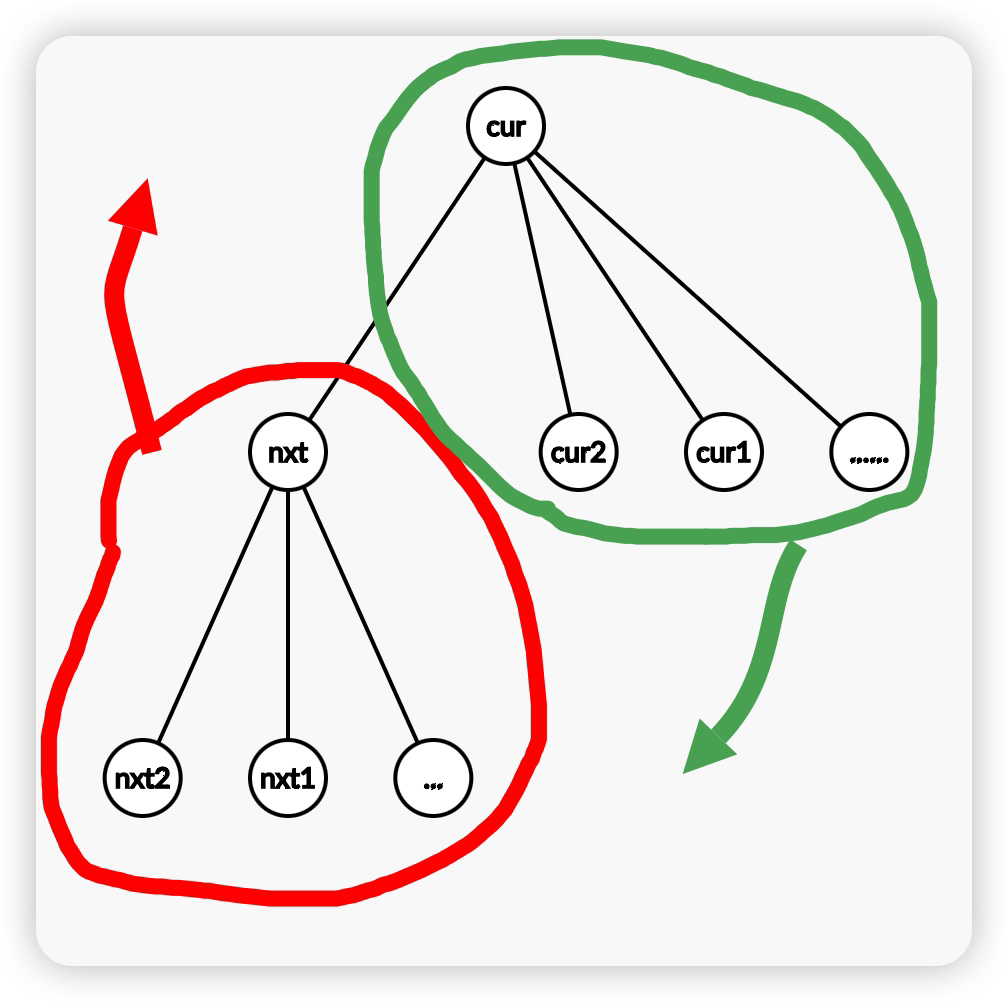
如图,以 \(nxt\) 为根的子树往上升,子树内贡献不变,且子树内的所有节点都无需经过 \(cur \to nxt\) 这条边;以 \(cur\) 为根的子树往下降,子树内的所有节点都必须经过 \(cur \to nxt\) 这条边。
于是有转移:
(\(w\) 表示 \(cur \to nxt\) 这条边的边权,\(siz_{nxt}\) 表示 \(nxt\) 子树内的牛的数量)
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5;
int n,tot,c[N];
struct E{ int v,w; };
vector<E> G[N<<1];
int dp[N],f[N],siz[N];
void dfs1(int cur,int fa){
siz[cur]=c[cur];
dp[cur]=0;
for(auto i:G[cur]){
if(i.v==fa) continue;
dfs1(i.v,cur);
siz[cur]+=siz[i.v];
dp[cur]+=dp[i.v]+siz[i.v]*i.w;
}
}
void dfs2(int cur,int fa){
for(auto i:G[cur]){
if(i.v==fa) continue;
f[i.v]=f[cur]+(tot-2*siz[i.v])*i.w;
dfs2(i.v,cur);
}
}
signed main(){
cin>>n;
for(int i=1;i<=n;i++)
cin>>c[i],tot+=c[i];
for(int i=1,u,v,w;i<n;i++)
cin>>u>>v>>w,
G[u].push_back({v,w}),
G[v].push_back({u,w});
dfs1(1,0);
f[1]=dp[1];
dfs2(1,0);
int ans=1e18;
for(int i=1;i<=n;i++)
ans=min(ans,f[i]);
cout<<ans;
return 0;
}
CF1187E
诈骗题。
我们先按照常规套路进行分析。
容易发现在第一次选点后的选点操作都是固定的。考虑换根 dp。
令 \(dp_i\) 表示以 \(i\) 为根的子树的全局最大权值(当然局部也可)。
初始:\(dp_{cur}=siz_{cur}\)(\(siz_i\) 表示以 \(i\) 为根的子树大小)。
转移:\(dp_{cur}=dp_{cur}+dp_i\)。
令 \(f_i\) 表示以 \(i\) 为全局根的最大权值。
初始:\(f_1=dp_1\)。
转移:
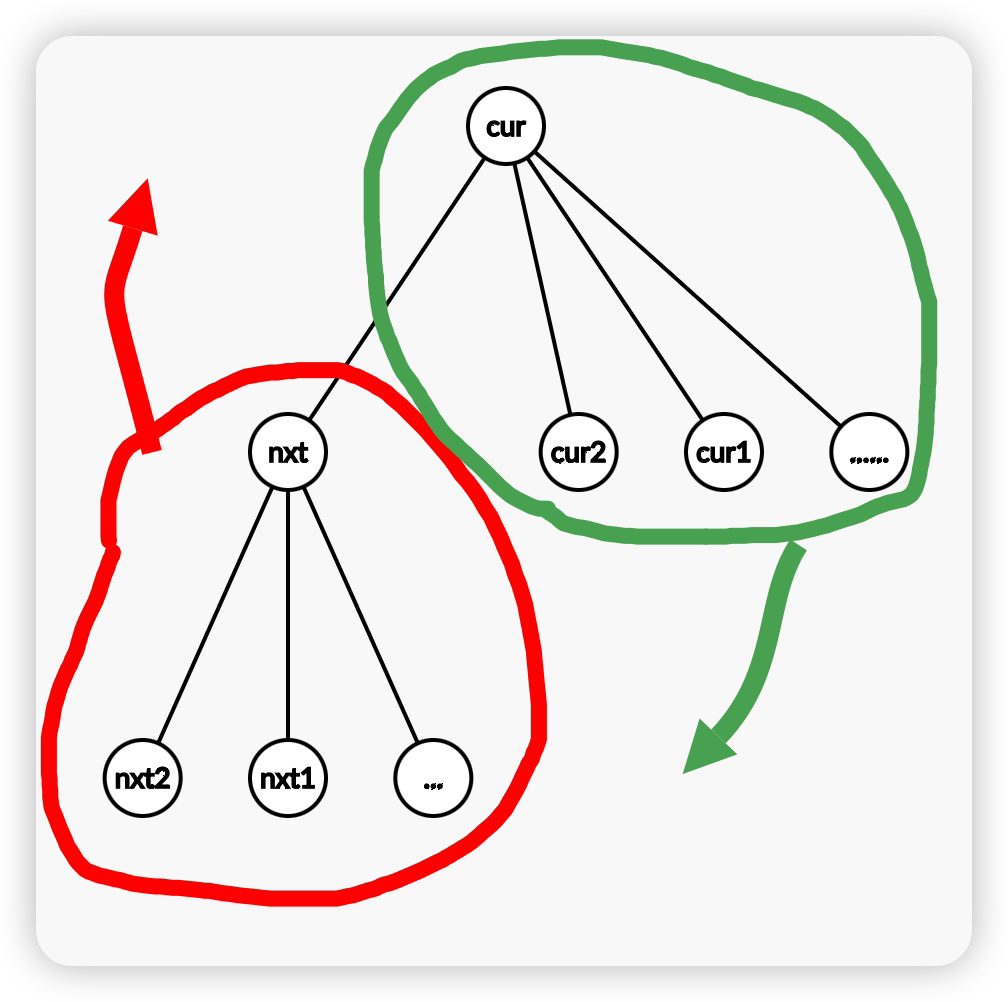
如图,以 \(nxt\) 为根的子树往上升,子树内贡献不变,且子树内所有节点均无需对以 \(cur\) 为根的子树产生贡献;以 \(cur\) 为根的子树往下降,子树内的所有节点都必须对以 \(nxt\) 为根的子树产生贡献。
于是有转移:
然后我们发现这就是 P3478 的转移方程。
这是因为每次进行染色,贡献都是染色节点的子树大小。
而每次染色后下一个被染色的一定是它的子节点,
这就导致每个节点在它的每一个祖先染色时都贡献了 \(1\),
加起来就是它的深度,
因此所有点的贡献之和就是深度之和。
code
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N=1e6+5;
int n;
vector<int> G[N<<1];
int dp[N],f[N],siz[N];
void dfs1(int cur,int fa){
siz[cur]=1;
for(int i:G[cur]){
if(i==fa) continue;
dfs1(i,cur);
siz[cur]+=siz[i];
dp[cur]+=dp[i];
}
dp[cur]+=siz[cur];
}
void dfs2(int cur,int fa){
for(int i:G[cur]){
if(i==fa) continue;
f[i]=f[cur]+n-2*siz[i];
dfs2(i,cur);
}
}
signed main(){
cin>>n;
for(int i=1,u,v;i<n;i++)
cin>>u>>v,
G[u].push_back(v),
G[v].push_back(u);
//dep[1]=1;
dfs1(1,0);
f[1]=dp[1];
dfs2(1,0);
int ans=0;
for(int i=1;i<=n;i++)
if(ans<f[i])
ans=f[i];
cout<<ans;
return 0;
}
CF1324F
看到 \(0,1\) 求贡献,首先考虑将 \(0\) 转化为 \(-1\)。
于是这题通过转化后,求差变为了求和。
接着我们发现,选包含某个点的连通子图,则必须包含其子树。
又因为要求出每个点的最大值,因此这题就变成了 换根版 的 最大子树和。
\(dp_i\) 按照那题求出即可。
令 \(f_i\) 表示以 \(i\) 为全局根的最大值。
初始:\(f_1=dp_1\)。
答案:所有的 \(f_i\)。
转移:
子树是必选的,子树外的如果贡献 \(>0\) 则可选,否则不选。
另外,子树外的贡献由子树内的贡献决定,如果子树内贡献 \(>0\),则子树外的要去掉子树内的贡献,否则它以前不会加上子树内的贡献,现在也不应当去掉。
于是有转移:
code
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+5;
int n,a[N];
int dp[N],f[N];
vector<int> G[N<<1];
void dfs1(int cur,int fa){
dp[cur]=a[cur];
for(int i:G[cur]){
if(i==fa) continue;
dfs1(i,cur);
dp[cur]=max(dp[cur],dp[cur]+dp[i]);
}
}
void dfs2(int cur,int fa){
for(int i:G[cur]){
if(i==fa) continue;
f[i]=dp[i]+max(f[cur]-max(dp[i],0),0);
dfs2(i,cur);
}
}
int main(){
cin>>n;
for(int i=1,x;i<=n;i++)
cin>>x,a[i]=(x?x:-1);
for(int i=1,u,v;i<n;i++)
cin>>u>>v,
G[u].push_back(v),
G[v].push_back(u);
dfs1(1,0);
f[1]=dp[1];
dfs2(1,0);
for(int i=1;i<=n;i++)
cout<<f[i]<<' ';
return 0;
}
