蒟蒻林荫小复习——树链剖分
快跑!这是林荫最想逃避的算法之一!
树链剖分——计算机术语,指一种对树进行划分的算法,它先通过轻重边剖分将树分为多条链,保证每个点属于且只属于一条链,然后再通过数据结构(树状数组、BST、SPLAY、线段树等)来维护每一条链。
前置芝士:
- DFS序
- 线段树
先来一道水题:
将树从x到y结点最短路径上所有节点的值都加上z
这个很好办,树上差分就可以解决这个林荫也不熟练
再来一个:求树从x到y结点最短路径上所有节点的值之和
这个也不错,先将点权转化为边权,同时维护树上点的深度,求LCA深度*2与两点深度作差即可。
但是要是将这两者结合起来怎么办?每次改变边权就DFS一次?那么N一次的改变会使你T上天。
_________________________________________林荫的分割线_____________________________________________________________
锵锵锵!树链剖分大魔王登场啦!
众所周知线段树可以维护一个数列的加减乘对吧,那么我们如果将这棵树拆成很多条链是不是就可以用线段树维护变化了呢?
那肯定是啊!
树剖是通过轻重边剖分将树分割成多条链,然后利用数据结构来维护这些链(本质上是一种优化暴力)
下个定义:
-
重儿子:父亲节点的所有儿子中子树结点数目最多(size最大)的结点;
-
轻儿子:父亲节点中除了重儿子以外的儿子;
-
重边:父亲结点和重儿子连成的边;
-
轻边:父亲节点和轻儿子连成的边;
-
重链:由多条重边连接而成的路径;
-
轻链:由多条轻边连接而成的路径;
先来一张网上广为流传的图:
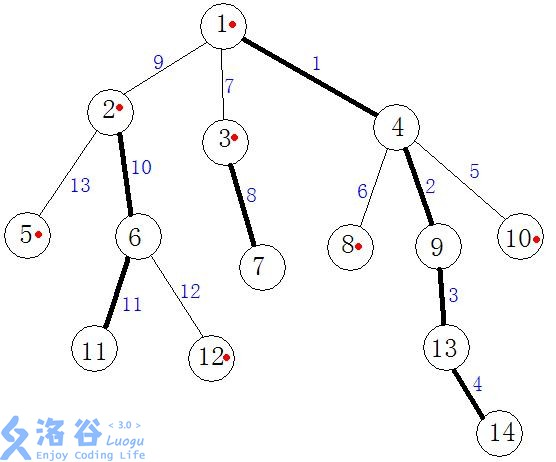
嗯,就是这样。
通过上面的定义,我们可以看到图中加黑的粗线就是重遍,重链也有3条。图中带有红点的点就是自己所在重链的起点,轻链上的叶子节点也是以自己为首的重链的起点哦(小小箍桶将,在家也是当家人/市长)
注意一下,图中边上的数字是DFS访问的顺序,点上的数字只是编号,至于像⑥的重儿子具体是11还是12这个倒是无所谓了。
struct PE { int sum,mx; }; PE t[120001]; int fa[30001],val[30001],size[30001],id[30001],rk[30001],son[30001],top[30001],dep[30001]; vector<int> b[30001];
声明变量:照样是网图(这份代码里面没写lazy标记)
| 名称 | 解释 |
| f[u] | 保存结点u的父亲节点 |
| d[u] | 保存结点u的深度值 |
| size[u] | 保存以u为根的子树节点个数 |
| son[u] | 保存重儿子 |
| rk[u] | 保存当前dfs标号在树中所对应的节点 |
| top[u] | 保存当前节点所在链的顶端节点 |
| id[u] |
保存树中每个节点剖分以后的新编号(DFS的执行顺序) |
好啦,这些变量中f,d,size,son都可以在第一次DFS中求出。
void dfs1(int x) { size[x]=1,d[x]=d[f[x]]+1; for(int v,i=head[x];i;i=e[i].next) if((v=e[i].to)!=f[x]) { f[v]=x,dfs1(v),size[x]+=size[v]; if(size[son[x]]<size[v]) son[x]=v; } }
处理出这些就是为了下面分出链做准备。
第二次DFS!
void dfs2(int x,int tp) { top[x]=tp,id[x]=++cnt,rk[cnt]=x; if(son[x]) dfs2(son[x],tp); for(int v,i=head[x];i;i=e[i].next) if((v=e[i].to)!=f[x]&&v!=son[x]) dfs2(v,v); }
在这次DFS中维护了重链上每个点的TOP,id和rk是用于维护线段树所必须的参数。(在线段树中所谓的区间就是指一段DFS序,那么x的所在位置就是id[x])
DFS跑完长这样!
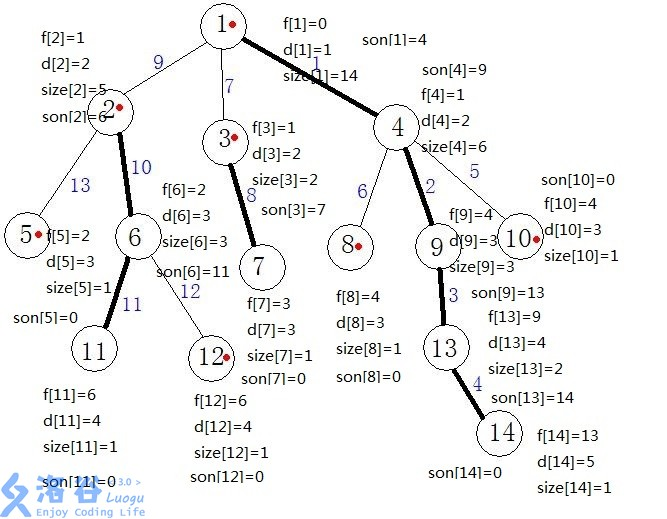
下面的话,线段树的基本操作大家都会吧,唯一有所不同的是,启动线段树上对于节点X的调用时,一定要记得带入对应的编号id[x];
void build(int x,int l,int r) { if(l==r) { t[x].sum=val[rk[l]]; t[x].mx=val[rk[l]]; return; } int mid=(l+r)>>1; build(x<<1,l,mid); build(x<<1|1,mid+1,r); t[x].sum=t[x<<1].sum+t[x<<1|1].sum; t[x].mx=max(t[x<<1].mx,t[x<<1|1].mx); }
如果要查询的两点在同一条链上就可以用线段树简单的解决,但如果不在同一条链上呢?
int Find(int x,int y) { int ans=-998244353; while(top[x]!=top[y]) { if(dep[top[x]]<dep[top[y]]) swap(x,y); ans=max(ans,queryx(1,1,n,id[top[x]],id[x])); x=fa[top[x]]; } if(dep[x]>dep[y]) swap(x,y); ans=max(ans,queryx(1,1,n,id[x],id[y])); return ans; }
这是一个查找两点间路径中最大值的一部分,queryx函数就是普通的线段树求最大值,下面解释一下其余部分。
因为这是一棵树,那么这两点一定会有LCA,而LCA一定会在一条链上,那么当两个点的top相同时就代表在同一条链上,那么就可以用线段树正常的解决。
当top不相等时,top更低的一个点向上移动到自己所在链的链首的上面的一个节点,即x=fa[top[x]]。但是被跳过的这一条链其中的贡献也一定会被计算,就直接计算x到top[x]的贡献即可。这样的话,就可以使得x和y到达同一条链上,然后让深度小的作为左边界,大的作为右边界进行线段树计算即可(因为DFS序在同一条链上是按照深度递增的,所以越靠下的节点DFS序越大)
放一个完整代码吧,洛谷模板题
代码和上面的片段不同,用的是动态开点,但是本质和大意是一样的哈。
#include<iostream> #include<cstdio> #define int long long using namespace std; const int maxn=1e5+10; struct edge{ int next,to; }e[maxn*2]; struct node{ int l,r,ls,rs,sum,lazy; }a[maxn*2]; int n,m,r,rt,mod,v[maxn],head[maxn],cnt,f[maxn],d[maxn],son[maxn],size[maxn],top[maxn],id[maxn],rk[maxn]; void add(int x,int y) { e[++cnt].next=head[x]; e[cnt].to=y; head[x]=cnt; } void dfs1(int x) { size[x]=1,d[x]=d[f[x]]+1; for(int v,i=head[x];i;i=e[i].next) if((v=e[i].to)!=f[x]) { f[v]=x,dfs1(v),size[x]+=size[v]; if(size[son[x]]<size[v]) son[x]=v; } } void dfs2(int x,int tp) { top[x]=tp,id[x]=++cnt,rk[cnt]=x; if(son[x]) dfs2(son[x],tp); for(int v,i=head[x];i;i=e[i].next) if((v=e[i].to)!=f[x]&&v!=son[x]) dfs2(v,v); } inline void pushup(int x) { a[x].sum=(a[a[x].ls].sum+a[a[x].rs].sum)%mod; } void build(int l,int r,int x) { if(l==r) { a[x].sum=v[rk[l]],a[x].l=a[x].r=l; return; } int mid=l+r>>1; a[x].ls=cnt++,a[x].rs=cnt++; build(l,mid,a[x].ls),build(mid+1,r,a[x].rs); a[x].l=a[a[x].ls].l,a[x].r=a[a[x].rs].r;//ls,rs指左右儿子,而l,r指以该节点为根的子树的区间。 pushup(x); } inline int len(int x) { return a[x].r-a[x].l+1; } inline void pushdown(int x) { if(a[x].lazy) { int ls=a[x].ls,rs=a[x].rs,lz=a[x].lazy; (a[ls].lazy+=lz)%=mod,(a[rs].lazy+=lz)%=mod; (a[ls].sum+=lz*len(ls))%=mod,(a[rs].sum+=lz*len(rs))%=mod; a[x].lazy=0; } } void update(int l,int r,int c,int x) { if(a[x].l>=l&&a[x].r<=r) { (a[x].lazy+=c)%=mod,(a[x].sum+=len(x)*c)%=mod; return; } pushdown(x); int mid=a[x].l+a[x].r>>1; if(mid>=l) update(l,r,c,a[x].ls); if(mid<r) update(l,r,c,a[x].rs); pushup(x);//只负责处理两点在同一条链上的情况。 } int query(int l,int r,int x) { if(a[x].l>=l&&a[x].r<=r) return a[x].sum; pushdown(x); int mid=a[x].l+a[x].r>>1,tot=0; if(mid>=l) tot+=query(l,r,a[x].ls); if(mid<r) tot+=query(l,r,a[x].rs); return tot%mod; } inline int sum(int x,int y) { int ret=0; while(top[x]!=top[y]) { if(d[top[x]]<d[top[y]]) swap(x,y); (ret+=query(id[top[x]],id[x],rt))%=mod; x=f[top[x]];//如果当前两者不在同一条重链上,就让深度大的一条一条重链向上跳,直到两者在一条重链上。 } if(id[x]>id[y]) swap(x,y); return (ret+query(id[x],id[y],rt))%mod; } inline void updates(int x,int y,int c) { while(top[x]!=top[y]) { if(d[top[x]]<d[top[y]]) swap(x,y); update(id[top[x]],id[x],c,rt); x=f[top[x]]; } if(id[x]>id[y]) swap(x,y); update(id[x],id[y],c,rt);//还是先跳到一条重链上,然后再计算在同一条链上的距离。 } int LINYIN() { scanf("%lld%lld%lld%lld",&n,&m,&r,&mod); for(int i=1;i<=n;i++) scanf("%lld",&v[i]); for(int x,y,i=1;i<n;i++) { scanf("%lld%lld",&x,&y); add(x,y),add(y,x); } cnt=0,dfs1(r),dfs2(r,r); cnt=0,build(1,n,rt=cnt++); for(int op,x,y,k,i=1;i<=m;i++) { scanf("%lld",&op); if(op==1) { scanf("%lld%lld%lld",&x,&y,&k); updates(x,y,k); } else if(op==2) { scanf("%lld%lld",&x,&y); printf("%lld\n",sum(x,y)); } else if(op==3) { scanf("%lld%lld",&x,&y); update(id[x],id[x]+size[x]-1,y,rt); } else { scanf("%lld",&x); printf("%lld\n",query(id[x],id[x]+size[x]-1,rt)); } } return 0; } int sddd=LINYIN(); signed main() { ; }
完结撒花!


