计算机体系结构-Booth乘法

浮点数

浮点数表示

浮点数主要包括符号位、基数、指数Exponent和尾数Mantissa部分组成。
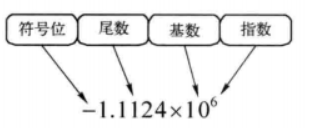
image

  • 尾数部分：小数部分，浮点数中表示精度的部分，通常用二进制表示小数，包含整数和小数部分，尾数确定了浮点数的有效数字位数和精度范围。浮点数的尾数可以表示为小于2的正数乘以2的幂次。对FP32而言，尾数通常由末23位二进制数表示。
  • 尾数运算规则：浮点数的尾数加法类似小数的加法，需要考虑舍入和规格化操作。浮点数的尾数乘法是将两个数的尾数相乘，将结果进行规格化和舍入。乘法操作会导致有效数字的尾数增加。
  • 指数部分（E）：阶码，对浮点数进行加权，使用k位进行编码的正数ek−1,ek−2,⋯,e0，采用无符号的解码方式

根据指数和尾数的不同取值，可以将浮点数分为规格化数、非规格化数和特殊值。

  • 规格化：E=exp-Bias，exp∈(0,2k−1),Bias=2k−1−1，可以将E重新投影到正负值，并和非规格化进行平滑转变。M=1+Frac，通过调整E可以实现1≤M≤2，将尾数变成1,fn−1,fn−2,⋯,f0的形式。
    -非规格化：exp=0,E=1−Bias，E=1−Bias,M=frac=0,fn−1,fn−2,⋯,f0。非规格化数能够表示正负0以及趋近于0的数，
  • 特殊值： exp全为1，frac全为0，表示无穷；exp全为1，frac不全为0，表示不存在的数，NAN。

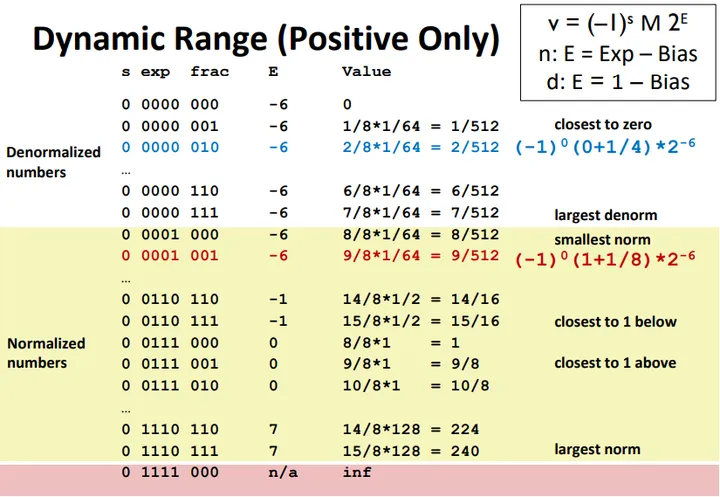
image

浮点数表示案例

image
image

浮点数计算特性

浮点数乘法

浮点数计算无法直接通过在位向量上运算得到。
浮点数乘法中(−1)s1×M1×2E1和(−1)s2×M2×2E2，计算结果为(−1)s×M×2E，其中s=s1⊕s2,M=M1×M2,E=E1+E2。

  • M大于2，那么需要将frac右移一位，并对E加1
  • E超出范围，则发生溢出，上溢得到INF，下溢得到0
  • M超出范围，则对frac进行舍入
  • 首先进行0检查，如果一个为0，则不进行浮点数乘法。
    数学性质主要为：
  • 可交换
  • 不可结合，结合可能会导致数值溢出和不精确的舍入
  • 不可分配，如果分配出现了NAN。

浮点数加法

对两个(−1)s1×M1×2E1和(−1)s2×M2×2E2，计算结果为(−1)s×M×2E，其中s和M为运算结果，E=max(E1,E2)，M=M1+M2。

  • 如果M≥2，则frac右移一位，并对E加1。
  • 如果M＜1，则frac左移一位，并对E减1。
  • 如果E超出范围则发生溢出；M超过表示范围则frac舍入。
    image

Booth乘法原理

电路实现

以Radix-4 Booth编码为例，Booth乘法的核心是部分积的生成，需要生成N/2个部分积，每个部分积与[X]补有关，存在−X,−2X,+X,+2X,0 这五种可能，其中减去X补的操作可以认为是按位取反的X补在末尾+1。为了硬件实现方便，可以将末位1操作提取出来，假设X补的二进制格式为x6x5x4x3x2x1x0，假设部分积P=p7p6p5p4p3p2p1p0+c，那么有：
image
当部分积微2X时，可以认为X输入左移一位，此时pi=xi−1相等。如果部分积的选择为−X/−2X，则此处对xi或xi−1取反，并设置最后的末位进位c=1。
由此可以得到每一位pi的逻辑表达式为：
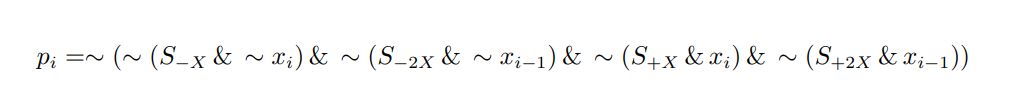
image
Booth结果选择逻辑如下所示：
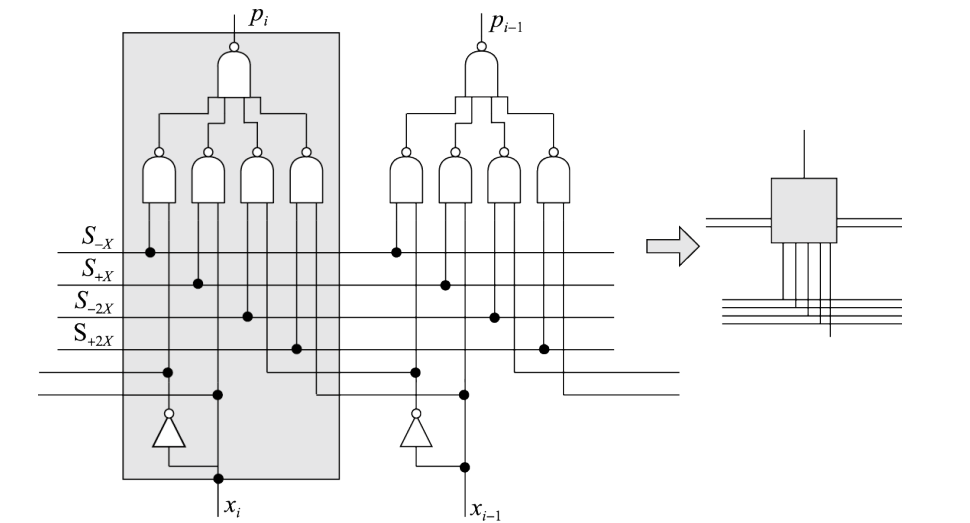
image

部分积生成过程中需要利用yi−1,yi和yi+1这三个信号来生成需要用到的S−X,S−2X,SX,S2x的选择信号，通过卡诺图化简可以得到：
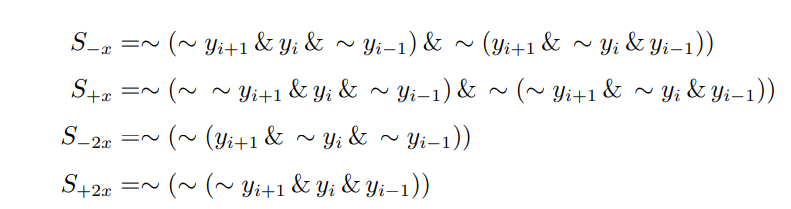
image
选择信号生成部分的逻辑图如下所示：
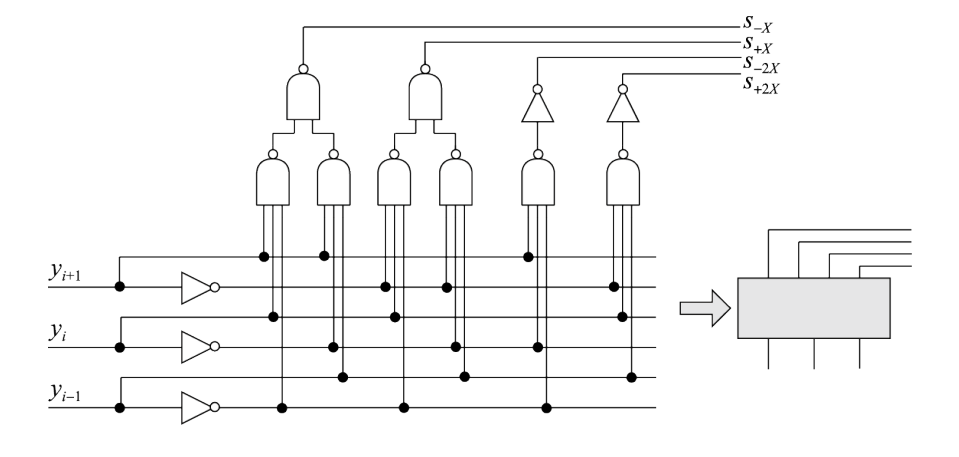
image
通过组合上述两个部分，可以形成每个Booth部分积的逻辑图，调用该逻辑通过移位加法策略可以实现两位Booth补码乘的结构。
乘法操作开始时，乘数右侧需要补1位的0，结果需要预置为全0.在每个时钟周期的计算结束后，乘数算术右移两位，被乘数左移两位，直到乘数全为0，乘法结束。
对于N位补码乘法，操作可以在N/2个时钟周期完成。被乘数、结果、加法器和Booth核心的宽度都为2N位。

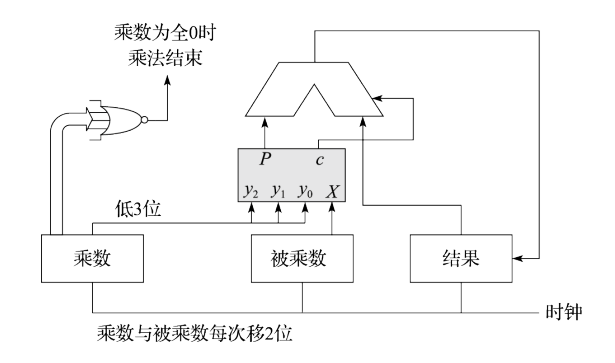
image
image

代码实现

Verilog

 
/*
* 基4的booth编码的单周期有符号乘法器
*/
 
module booth_multiplier_base4 #(
    parameter DATA_WIDTH = 8       // 数据位宽应该为2的指数
)
 
(  
    input [DATA_WIDTH-1 : 0] a,  
    input [DATA_WIDTH-1 : 0] b,  
    output reg [2*DATA_WIDTH-1 : 0] product,
    input clk
);  
  
    integer i;  
    reg [2:0] booth_bits [DATA_WIDTH/2-1:0];  
    reg [DATA_WIDTH:0] b_extended;
    reg [2*DATA_WIDTH:0] partial_product [DATA_WIDTH/2-1:0];  
    reg [2*DATA_WIDTH-1:0] a_pos, a_neg, a_extend; 
  
    always @(posedge clk) begin  
        b_extended = {b, 1'b0}; // 这里我补了个0，防止索引超出界限
        a_extend = {{DATA_WIDTH{a[DATA_WIDTH-1]}}, a};    // 符号位扩展 ，之前忘记扩展找了好久
        a_pos = a_extend;
        a_neg = ~a_extend + 1'b1;  // 补码运算
        product = 0;
 
        for (i = 0; i < DATA_WIDTH/2; i = i + 1) begin  
            booth_bits[i] = {b_extended[2*i+2], b_extended[2*i+1], b_extended[2*i]};  
 
            case (booth_bits[i])
            /*
            $\sum_{i=0}^{\frac{n}{2}-1} (-2 \cdot b_{2i+2} + b_{2i+1} + b_{2i})$  // LaTex
            { b(2i+2), b(2i+1), b(2i) } :=
                000:    0;
                001:    1;
                010:    1;
                011:    2;
                100:    -2;
                101:    -1;
                110:    -1;
                111:    0;
            */  
                3'b000, 3'b111: partial_product[i] = 9'd0;  
                3'b001, 3'b010: partial_product[i] = a_pos;
                3'b011:         partial_product[i] = a_pos << 1;
                3'b100:         partial_product[i] = a_neg << 1;
                3'b101, 3'b110: partial_product[i] = a_neg; 
            endcase  
        end
 
        for (i = 0; i < (DATA_WIDTH/2-1); i = i + 1) begin
            product = product + (partial_product[i] << (2*i)); // Shift and accumulate
        end
            
          
 
    end  
  
endmodule

下面为testbench

`timescale 1ns/1ns
 
module sim_booth_multiplier_base4 ();
 
parameter DATA_WIDTH = 8;    
 
reg [DATA_WIDTH-1:0] a;
reg [DATA_WIDTH-1:0] b;
wire [2*DATA_WIDTH-1:0] product;
reg [2*DATA_WIDTH-1:0] expected_product;
reg test_passed;
reg clk;
 
booth_multiplier_base4 #(.DATA_WIDTH(DATA_WIDTH)) booth_multiplier_base4_0
(
    .a(a),
    .b(b),
    .product(product),
    .clk(clk)
);
 
initial begin  
    // 初始化  
    $display("Time, a, b, Expected Product, Actual Product, Test Result\n");  
    clk = 0;
    // 第一个样例  
    a <= 8'b01111111; // 127  
    b <= 8'b00000010; // 2  
    expected_product <= 16'd254; // 254  
    #10; // 等待一些时间以便观察波形  
    test_passed = (product == expected_product) ? 1 : 0;  
    $display("%d, %b, %b, %b, %b, %s\n", $time, a, b, expected_product, product, (test_passed ? "PASSED" : "FAILED"));  
 
    // 第二个样例 (注意：在实际八位乘法中这是不可能的，因为会溢出)  
    // 我们可以故意让它失败，或者用一个能够处理溢出的乘法器  
    a <= 8'b10000000; // -128 (补码表示)  
    b <= 8'b10000000; // -128 (补码表示)  
    // 由于这个乘法实际上会溢出，所以设置expected_product为一个不可能的值  
    expected_product <= 16'bx0000000000000000; // 'x'表示不关心这些位  
    #10;  
    // 这里我们检查乘法器是否设置了溢出标志位（如果有的话），或者检查最高位是否设置正确  
    // 由于我们没有具体的乘法器实现细节，这里只能做一个假设性的检查  
    // 假设乘法器在溢出时将最高位设置为1  
    test_passed = (product == expected_product) ? 1 : 0;  
    $display("%d, %b, %b, %b, %b, %s (Overflow Expected)\n", $time, a, b, expected_product, product, test_passed ? "PASSED" : "FAILED");  
 
    // 第三个样例  
    a <= 8'b11111111; // -1  
    b <= 8'b11111111; // -1  
    expected_product <= 16'b0000000000000001; // 1  
    #10;  
    test_passed = (product == expected_product) ? 1 : 0;  
    $display("%d, %b, %b, %b, %b, %s\n", $time, a, b, expected_product, product, test_passed ? "PASSED" : "FAILED");  
 
    // 结束仿真  
    $finish;  
end  
 
always begin
    #2;
    clk = ~clk;
end
endmodule

Chisel实现

import chisel3._  
import chisel3.util._  
  
class BoothMultiplierBase4(val DATA_WIDTH: Int = 8) extends Module {  
  val io = IO(new Bundle {  
    val a = Input(SInt(DATA_WIDTH.W))  // Signed input a  
    val b = Input(SInt(DATA_WIDTH.W))  // Signed input b  
    val product = Output(SInt((2 * DATA_WIDTH).W)) // Signed output product  
  })  
  
  val booth_bits = Wire(Vec((DATA_WIDTH / 2), UInt(3.W)))  
  val partial_products = RegInit(VecInit(Seq.fill(DATA_WIDTH / 2)(0.S((2 * DATA_WIDTH).W))))  
  
  // On every positive edge of the clock  
 
  val b_extended = io.b << 1.U // Sign-extend b with an extra 0  
  val a_neg = -io.a                    // Negation of a  
  val a_pos = io.a                     // Positive of a
  val regProduct = RegInit(0.S((2 * DATA_WIDTH).W))
 
  // Calculate Booth bits  
  for (i <- 0 until DATA_WIDTH / 2) {  
    booth_bits(i) := Cat(b_extended(2*i+2), b_extended(2*i+1), b_extended(2*i)) 
 
    // Calculate partial products based on Booth encoding  
    partial_products(i) := MuxCase(0.S, Array(  
      (booth_bits(i) === 0.U || booth_bits(i) === 7.U) -> 0.S,  
      (booth_bits(i) === 1.U || booth_bits(i) === 2.U)  -> a_pos,  
      (booth_bits(i) === 3.U) -> (a_pos << 1.U),  
      (booth_bits(i) === 4.U) -> (a_neg << 1.U),                 // 此处自动进行符号位的扩展，下同
      (booth_bits(i) === 5.U || booth_bits(i) === 6.U) -> a_neg  
    ))  
  }  
 
  // Accumulate partial products to form the final product  
 
  io.product := partial_products.zipWithIndex.map{
    case (pp, i) => pp << ((2*i).U)
  }.reduce(_+_)
 
  
 
}  
  
/* An object extending App to generate the Verilog code*/
object BoothMultiplierBase4 extends App {
  (new chisel3.stage.ChiselStage).emitVerilog(new BoothMultiplierBase4(), Array("--target-dir", "./verilog/BoothMultiplier"))
}

下面为testbench

 
import org.scalatest.flatspec.AnyFlatSpec  
import scala.util.Random  
import chisel3._  
import chisel3.tester._  
 
// Booth乘法器的测试类  
 
  
class BoothMultiplierBase4Test extends AnyFlatSpec with ChiselScalatestTester {  
    behavior of "BoothMultiplierBase4"  
    
    it should "multiply signed numbers correctly" in {  
        for (i <- 0 until 10) {  
            val a = Random.nextInt(256) - 128 // 生成-128到127之间的随机数  
            val b = Random.nextInt(256) - 128  
    
            test(new BoothMultiplierBase4) { c =>  
                c.io.a.poke(a.S) // 将随机数a作为有符号数输入  
                c.io.b.poke(b.S) // 将随机数b作为有符号数输入  
                c.clock.step(2) // 时钟前进一步以执行乘法  
        
                val expectedProduct = a.toLong * b.toLong // 计算预期乘积  
                val actualProduct = c.io.product.peek().litValue.toLong // 获取实际乘积  
                /* 
                    c: 这是测试环境中BoothMultiplierBase4模块的实例。
                    c.io.product: 这是指向模块输出端口product的引用。
                    peek(): 这是一个Chisel测试方法，用于在不推进时钟的情况下读取端口的当前值。
                    litValue: 这是一个方法，用于从Chisel的Data类型中提取实际的Scala值（在这个例子中是BigInt） 
                */
                
                println(s"Iteration: $i, A: $a, B: $b, Expected Product: $expectedProduct, Actual Product: $actualProduct")  
 
                assert(actualProduct === expectedProduct, s"Product is incorrect at iteration $i! Expected: $expectedProduct, Actual: $actualProduct")  
        
                
            }  
        }  
    }  
}

浮点数-Booth实现
https://blog.csdn.net/weixin_45937291/article/details/124192302

posted @   信海  阅读(377)  评论(0)  编辑  收藏  举报
相关博文：
·  HARDWAR FOR ML- LECTURE 6 DATAFLOW
·  贝叶斯推断架构实现
·  C--密码学高级教程-全-
·  计算机组成原理【3】：数据的表示和运算-下
·  浮点数的加减乘除运算细节
阅读排行：
· 10年+ .NET Coder 心语 ── 封装的思维：从隐藏、稳定开始理解其本质意义
· 提示词工程——AI应用必不可少的技术
· 地球OL攻略 —— 某应届生求职总结
· 字符编码：从基础到乱码解决
· SpringCloud带你走进微服务的世界
点击右上角即可分享
微信分享提示
AI IDE Trae