HARDWAR FOR ML- LECTURE 6 DATAFLOW
Review
Deep neural networks typically have a sequence of convolutional,fully-connected, pooling, batch normalization, and activation layers.
Convolution is one of the fundamental kernel in DNNs.
- 2-D convolution
- Stride and padding
- 3-D convolution with input/output channels·Batch size
Convolution can be calculated in different ways.
- Direct, GEMM, FFT-based, Winograd-based
Convolution Loop Nest
Option 1: Direct Convolution

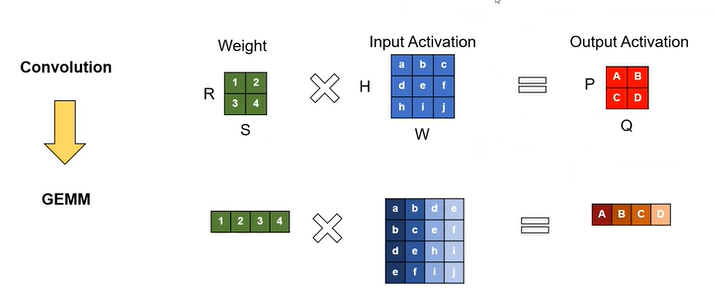
Option 2:GEMM
由于直接卷积的计算效率并不高,Option 2是通过im2col(python存在相应的函数)将卷积运算转换为GEMM。矩阵乘法具有较多的开发经验,直接开发卷积加速软硬件核较为困难。这种方法主要是将卷积窗口对应的局部视野展开为列,将多个卷积窗口内的输入激活展开为多列元素。
主要缺陷:增加了输入激活的memory占用,需要重新组织输入的数据流(元素沿副对角线对称分布)。
通用矩阵乘法的优化可见: https://blog.csdn.net/qq_35985044/article/details/128474264
除了上述方式以外,我们还可以尝试下述这种对角映射方案。以\(H\times W\)的输入图像和尺寸为\(Kh\times Kw\)的卷积核(步长为1,padding为0)为例,输入尺寸为\(H=W=100\),卷积核尺寸为\(Kh=Kw=3\)。
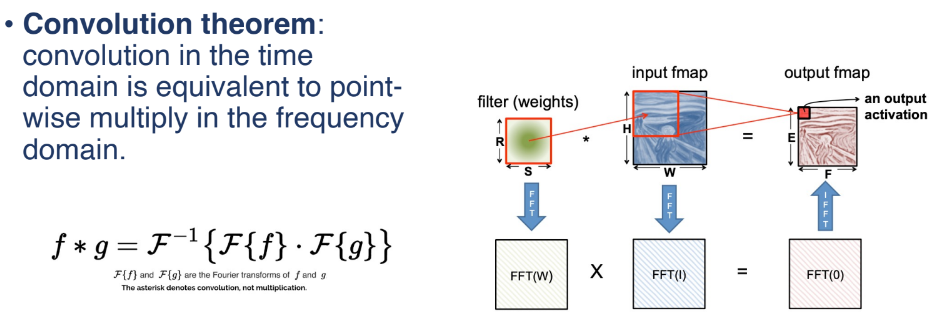
Option 3: FFT-based Convolution
FFT方法是将时域的卷积运算转换为频域的点乘运算,因此需要对权重和输入特征图进行FFT变换得到频域输入和权重,通过乘法得到输出激活的频域表示,最后通过反傅里叶变换恢复输出激活的真实输出。
#!/user/bin/env python3 # -*- coding: utf-8 -*- from functools import partial from typing import Iterable, Tuple, Union import torch import torch.nn.functional as f from torch import Tensor, nn from torch.fft import irfftn, rfftn from math import ceil, floor def complex_matmtul(a: Tensor, b: Tensor, groups: int = 1) -> Tensor: """ :param a: :param b: :param groups: grouped multiplications support multiple sections of channels :return: """ a = a.view(a.size(0), groups, -1, *a.shape[2:]) b = b.view(groups, -1, *b.shape[1:]) a = torch.movedim(a, 2, a.dim() - 1).unsqueeze(-2) b = torch.movedim(b, (1, 2), (b.dim() - 1, b.dim() - 2)) real = a.real @ b.real - a.imag @ b.imag imag = a.imag @ b.real + a.imag @ b.imag real = torch.movedim(real, real.dim() - 1, 2).squeeze(-1) imag = torch.movedim(imag, imag.dim() - 1, 2).squeeze(-1) c = torch.zeros(real.shape, dtype=torch.complex64, device=a.device) c.real, c.imag = real, imag return c.view(c.size(0), -1, *c.shape[3:]) def to_ntuple(val: Union[int, Iterable[int]], n: int) -> Tuple[int, ...]: """ :param val: :param n: :return: """ if isinstance(val, Iterable): out = tuple(val) if len(out) == n: return out else: raise ValueError(f"Cannot cast tuple of length {len(out)} to length {n}.") else: return n * (val,) def fft_conv( signal: Tensor, kenerl: Tensor, bias: Tensor, padding: Union[int, Iterable[int], str] = 0, padding_mode: str = "constant", stride: Union[int, Iterable[int]] = 1, dilation: Union[int, Iterable[int]] = 1, groups: int = 1 ) -> Tensor: """ :param signal: Input tensor to be convolved with the kernel :param kenerl: convolution kernel :param bias: bias tensor to add to the output :param padding: If int, number of zero samples to pad input on the last dimension; If str "same", pad input for size preservation :param padding_mode: padding_mode: use {constant, reflection, replication} :param stride: (Union[int, Iterable[int]]) Stride size for computing output values :param dilation: (Union[int, Iterable[int]]) Dilation rate for the kernel :param groups: Number of groups for the convolution :return: """ # Cast padding, stride & dilation tu tuples n = signal.dim - 2 stride_ = to_ntuple(stride, n=n) dilation_ = to_ntuple(dilation, n=n) if isinstance(padding, str): if padding == 'same': if stride != 1 or dilation != 1: raise ValueError("stride must be 1 for padding = 'same'.") padding_ = [(k - 1) / 2 for k in kenerl.shape[2:]] else: raise ValueError(f"Padding mode {padding} not supported") else: padding_ = to_ntuple(padding, n=n) # internal dilation offsets offset = torch.zeros(1, 1, *dilation_, device=signal.device, dtype=signal.dtype) offset[(slice(None), slice(None), *((0,) * n))] = 1.0 # correct the kernel by cutting off unwanted dilation trailing zeros cutoff = tuple(slice(None, -d + 1 if d != 1 else None) for d in dilation_) # create tuple # pad the kernel internally according to the dilation parameters kernel = torch.kron(kenerl, offset)[(slice(None), slice(None)) + cutoff] # after dilation # Pad the input signal & kernel tensors (round to support even sized convolutions) signal_padding = [r(p) for p in padding_[::-1] for r in (floor, ceil)] signal = f.pad(signal, signal_padding, mode=padding_mode) signal_size = signal.size() # original signal size without padding to even if signal.size(-1) % 2 != 0: signal = f.pad(signal, [0, 1]) kernel_padding = [ pad for i in reversed(range(2, signal.ndim)) for pad in [0, signal.size(i) - kernel.size(i)] ] # (H - Kh) * (W - Kw) padded_kernel = f.pad(kernel, kernel_padding) # input_channels * output_channels * H * W # Perform Fourier convolution FFT matrix multiply IFFT signal_fr = rfftn(signal.float(), dim=tuple(range(2, signal.ndim))) kernel_fr = rfftn(padded_kernel.float(), dim=tuple(range(2, signal.ndim))) kernel_fr.imag *= -1 output_fr = complex_matmtul(signal_fr, kernel_fr, groups=groups) output = irfftn(output_fr, dim=tuple(range(2, signal.ndim))) # Remove extra padded values crop_slices = [slice(None), slice(None)] + [ slice(0, (signal_size[i] - kernel.size(i) + 1), stride_[i - 2]) for i in range(2, signal.ndim) ] output = output[crop_slices].contiguous() if bias is not None: bias_shape = tuple([1, -1] + (signal.ndim - 2) * [1]) # 1 * -1 * 1 * 1 output += bias.view(bias_shape) return output class _FFTConv(nn.Module): def __init__(self, in_channels: int, out_channels: int, kernel_size: Union[int, Iterable[int]], padding: Union[int, Iterable[int]] = 0, padding_mode: str="constant", stride: Union[int, Iterable[int]] = 1, dilation: Union[int, Iterable[int]] = 1, groups: int = 1, bias: bool = True, ndim: int = 1): super().__init__() self.in_channels = in_channels self.out_channels = out_channels self.kernel_size = kernel_size self.padding = padding self.padding_mode = padding_mode self.stride = stride self.dilation = dilation self.groups = groups self.use_bias = bias if in_channels % groups != 0: raise ValueError( "'in_channels' must be divisible by 'groups'." f"Found: in_channels={in_channels}, groups={groups}." ) if out_channels % groups != 0: raise ValueError( "'out_channels' must be divisible by 'groups'." f"Found: out_channels={out_channels}, groups={groups}." ) kernel_size = to_ntuple(kernel_size, ndim) weight = torch.randn(out_channels, in_channels // groups, *kernel_size) self.weight = nn.Parameter(weight) self.bias = nn.Parameter(torch.randn(out_channels)) if bias else None def forward(self, signal): return fft_conv( signal, self.weight, bias=self.bias, padding=self.padding, padding_mode=self.padding_mode, stride=self.stride, dilation=self.dilation, groups=self.groups, ) FFTConv1d = partial(_FFTConv, ndim=1) FFTConv2d = partial(_FFTConv, ndim=2) FFTConv3d = partial(_FFTConv, ndim=3)
下面给出测试代码:
import torch from fft_conv import fft_conv, FFTConv1d signal = torch.randn(3, 3, 1024) # data shape: (batch, channels, length) kernel = torch.randn(2, 3, 128) # kernel shape: (out_channels, in_channels, kernel_size) bias = torch.randn(2) out = fft_conv(signal, kernel, bias=bias) fft_conv = FFTConv1d(3, 2, 128, bias=True) fft_conv.weight = torch.nn.Parameter(kernel) fft_conv.bias = torch.nn.Parameter(bias) out = fft_conv(signal) print(f"Output shape: {out.shape}")
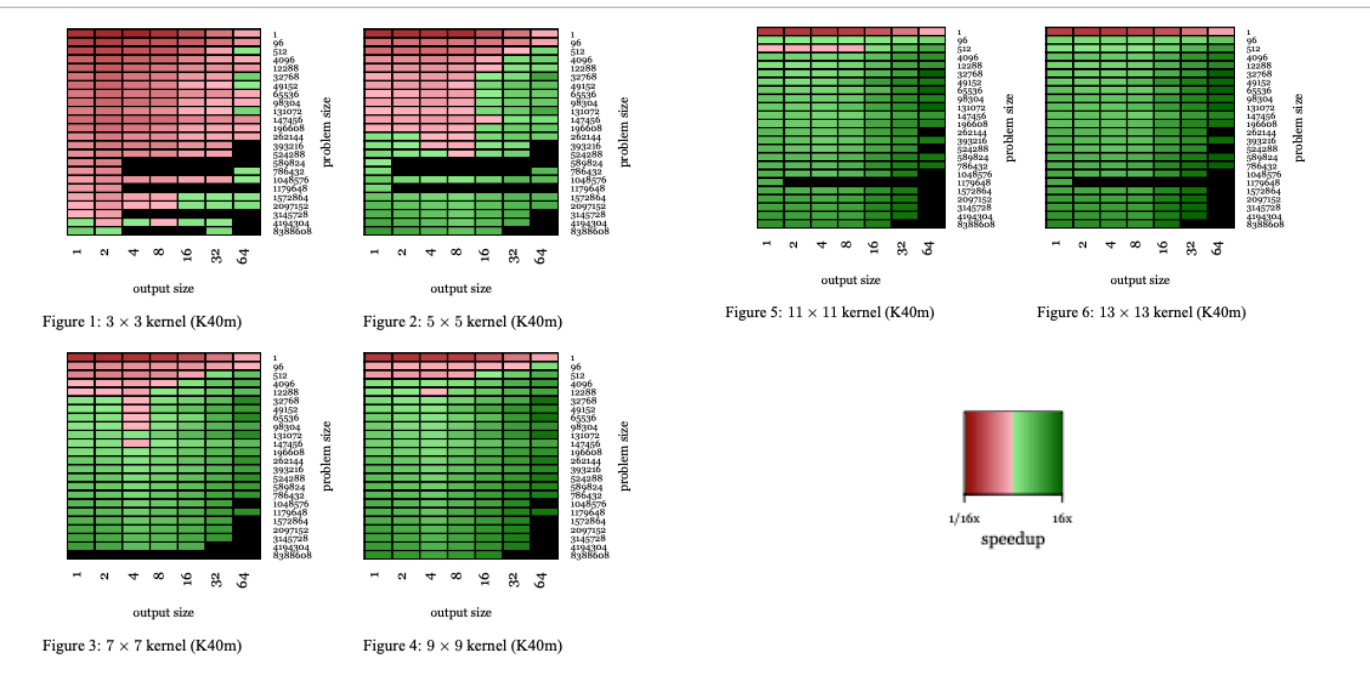
可以注意到的是,在卷积核计算中FFT-based方法比Direct convolution更具有speedup优势。
Option 4: Winograd Transform
以下图中的一维卷积为例,一般矩阵乘法需要进行6次乘法和4次加法。

卷积运算中输入信号转换成的矩阵不是任意矩阵,其中有规律地分布大量元素,第一行和第二行中的\(d_1\)和\(d_2\),卷积转换成的矩阵乘法比一般矩阵乘法的问题域更小。
Winograd引入\(m_1\sim m_4\)来参与计算,计算\(r_0=m_1+mm_2+m_3,r_1=m_2-m_3-m_4\)需要在输入信号\(d\)上消耗4次加法(减法),输出\(m\)上需要消耗4次乘法和4次加法。
由于神经网络推理时,卷积核元素是固定的,因此\(g\)上的运算可以提前算好,预测阶段只需要计算一次,可以忽略\(g\)的计算(三次加法,\(g_0+g_2\)为1次,\(g_0+g_2-g_1\)和\(g_0+g_2+g_1\)为1次),总共需要的运算次数为4次乘法和8次加法。计算机中,乘法比加法慢,减少乘法次数,增加少量加法可以实现加速。
我们可以将Winograd过程表述为下述矩阵形式(\(G,B^T\)为对\(g\)和\(d\)的变换算子),具体包括输入变换、卷积核变换、哈达马积、输出变换:

如何将Winograd推广到二维?可以使用\(Y=A^T[[GgG^T]\odot [B^TdB]] A\),\(g\)为\(r\times r\)卷积核,\(d\)为\((m+r-1)\times (m+r-1)\)的image tiles.
对于1维卷积\(F(m,r)\)的Winograd算法,其需要的乘法个数为\(m+r−1\)。对于2维卷积\(F(m\times n,r\times s)\)的Winograd算法,其需要的乘法个数为\((m+r-1)\times(n+s-1)\)。当n = m n=mn=m以及\(s=r\)时,卷积\(F(m\times m,r\times r)\)的Winograd算法需要的乘法个数为\((m+r-1)\times(m+r-1)\)。推导手稿可见下面


其他信息补充
Dilation
在卷积神经网络(CNN)中,膨胀(dilation)是一种用于增加卷积操作感受野的技术。通常情况下,卷积操作在输入张量上以固定的步幅滑动,以便从每个位置提取信息。然而,通过引入膨胀参数,可以使卷积核在输入张量上以更大的步幅滑动,从而扩大其感受野。
具体来说,膨胀操作会在卷积核中的元素之间插入额外的零值,这样就扩大了卷积核的有效大小,使其在输入张量上的感受野变大。这样做的一个重要优点是,在不增加卷积核大小的情况下,可以增加网络的感受野,从而更好地捕捉输入数据的长程依赖关系和上下文信息。
膨胀在卷积神经网络中的应用有以下几个方面的作用:
增大感受野:通过增加卷积核的有效大小,可以在不增加参数数量的情况下扩大网络的感受野,使网络能够更好地理解输入数据的整体结构和上下文信息。
减少参数数量:相比于传统的卷积操作,膨胀卷积可以在不增加参数数量的情况下增大感受野,因为它只是通过插入零值来改变卷积核的行为,而不是增加额外的权重参数。
提高计算效率:由于膨胀卷积可以在更大的步幅下滑动,因此可以在一定程度上减少计算量,提高模型的计算效率。
总的来说,膨胀在卷积神经网络中被用来扩大网络的感受野,从而增强网络对输入数据的理解能力,同时又不增加太多的参数数量和计算成本。
Dataflow Taxonomy
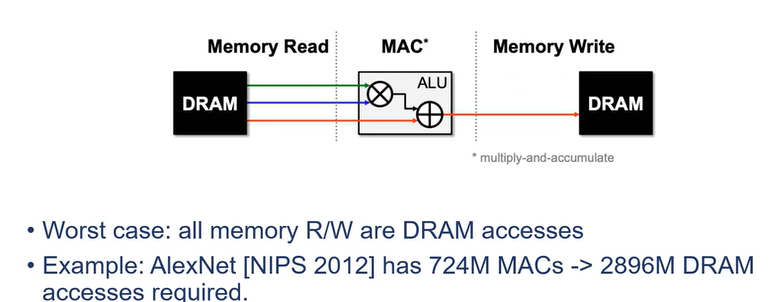
Locality主要反映在内存访存模式和时空数据重用。
- 内存访存涉及内存memory read,mac和memory write。内存访存次数远大于Mac次数。
- 时空数据重用体现为数据缓存的时分复用或空分复用。
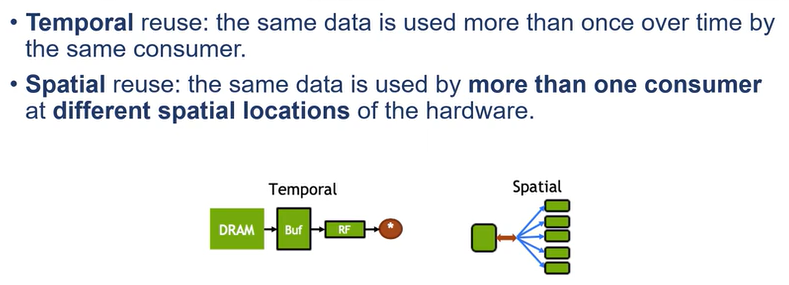
针对temporal和spatial locality的改进方法:
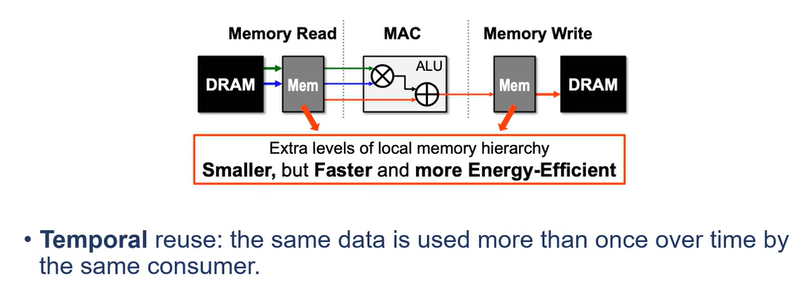
内存时分复用中的改进方法可以建立memory hierarchy,通过在计算单元和DRAM中间引入一个较小的、速度更快的cache来实现数据的缓冲,便于DNNs计算中的数据重用。
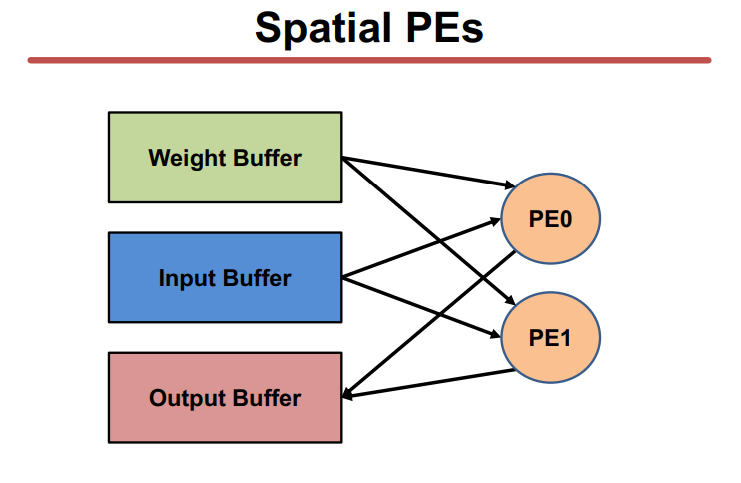
空分复用的典型方法是建立并行的计算单元来提高吞吐量。【the same data is used by more than one consumer at different spatial locations of the hardware.】
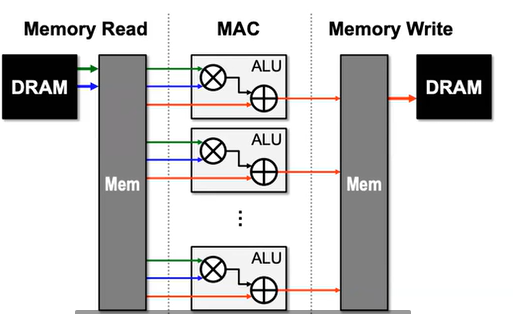
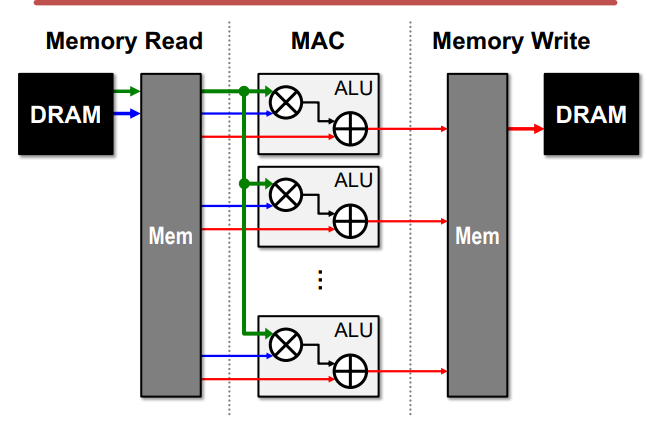
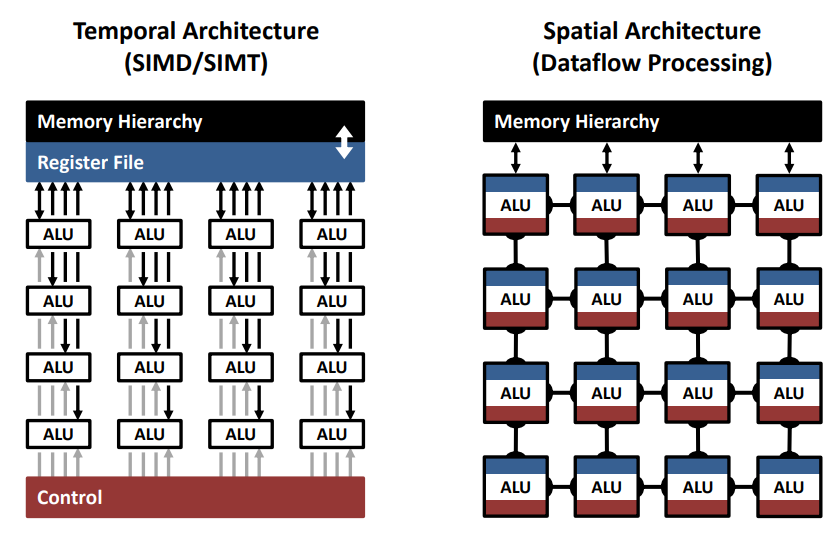
Locality and Parallisim是提高性能的主要方法。
Data Reuse in DNN
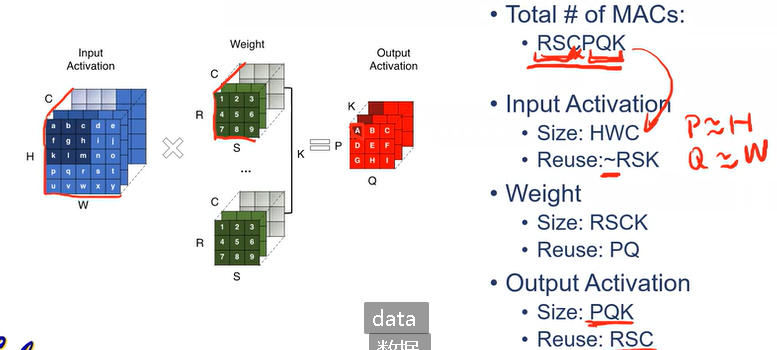
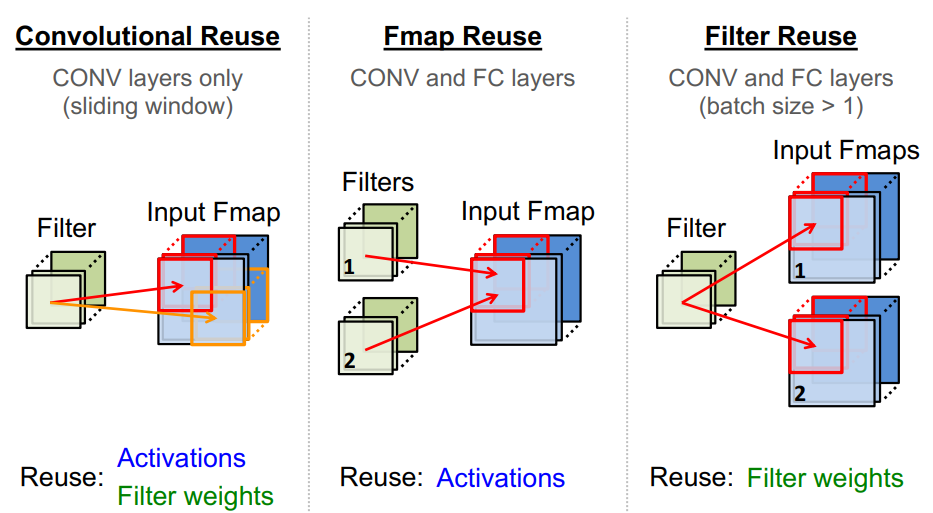
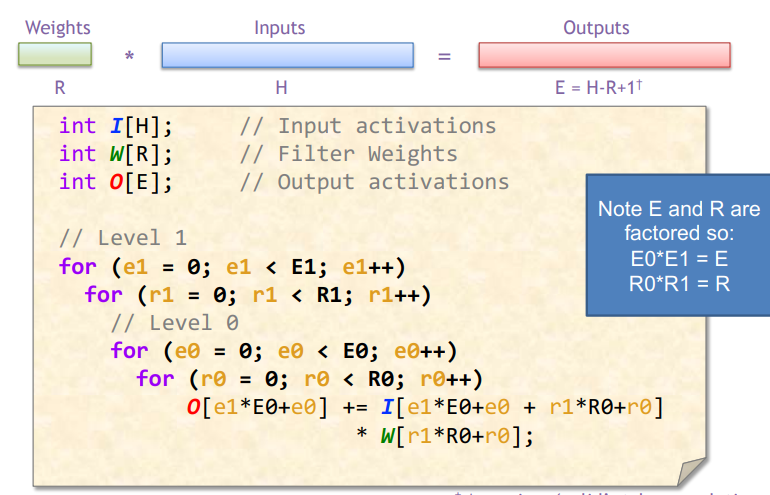
Dataflow: 决定硬件中DNN操作的执行顺序,包括计算顺序或数据移动顺序。
Loop nest:一种紧凑的方式来描述执行顺序(这里讨论的不是严格的体系结构中数据分布概念)。例如,dataflow (for表示temporal,描述时序执行顺序;spatial_for用于描述并行顺序)。
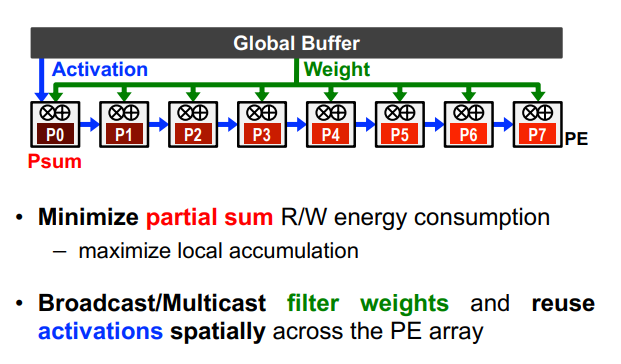
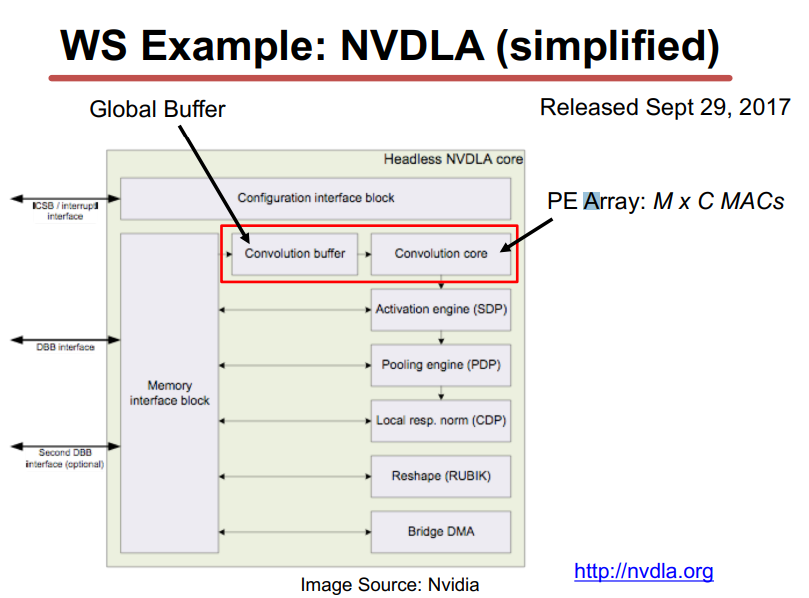
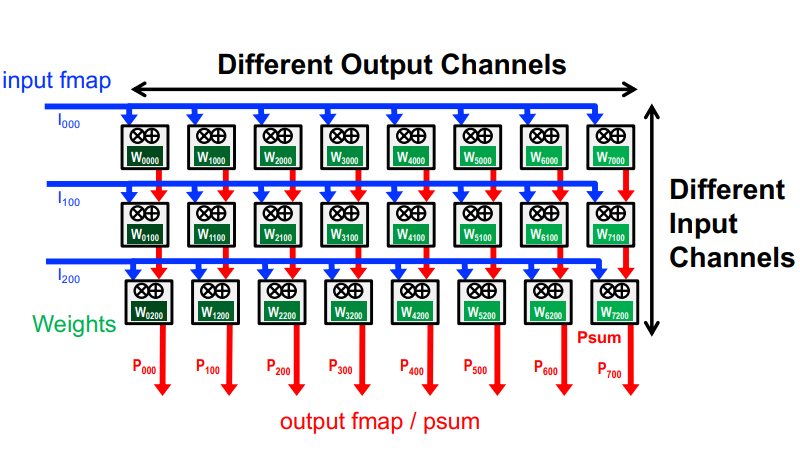
Output-Stationary and Weight-Stationart

WS和OS取决于loop nest的最内层循环,其中不变的量为静止对象,输出激活是保持不变的。
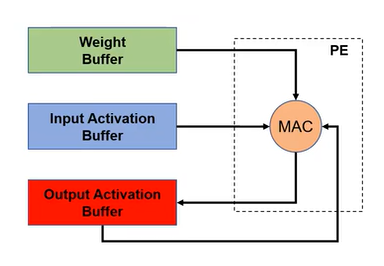
OS
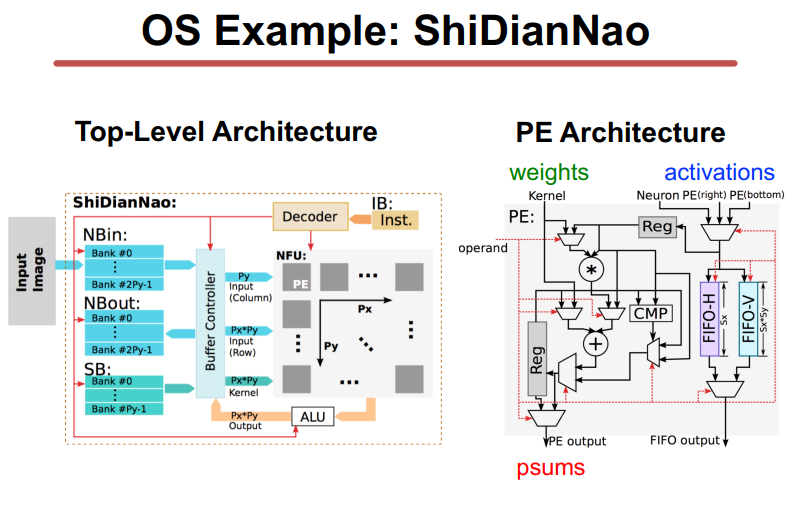
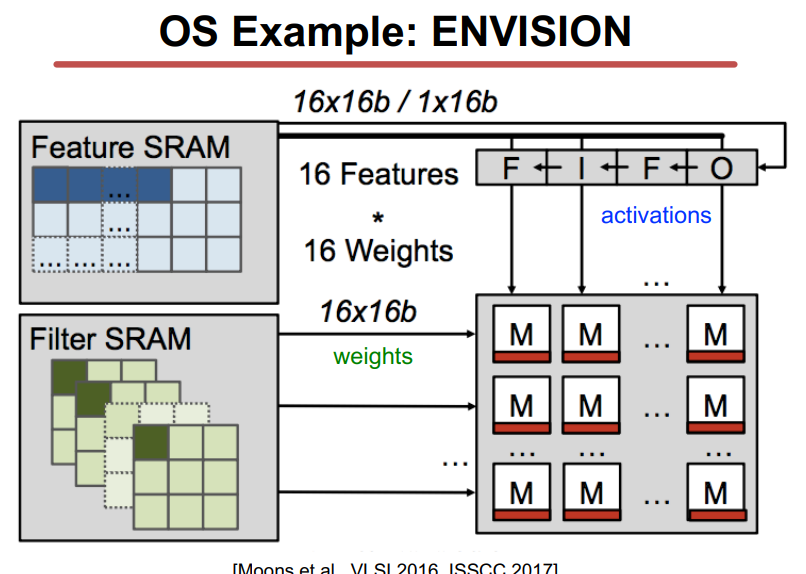
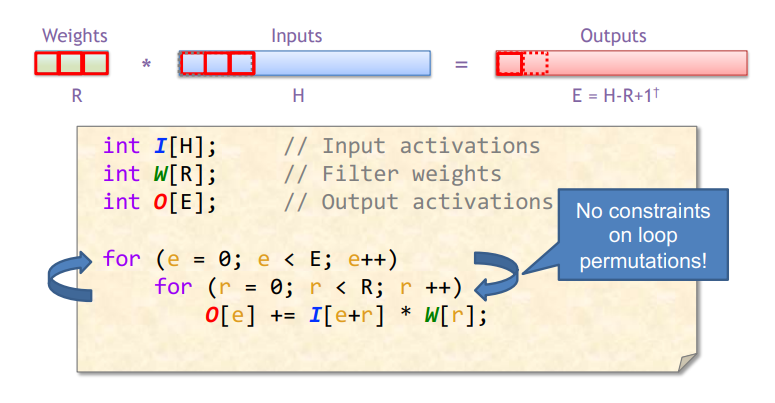
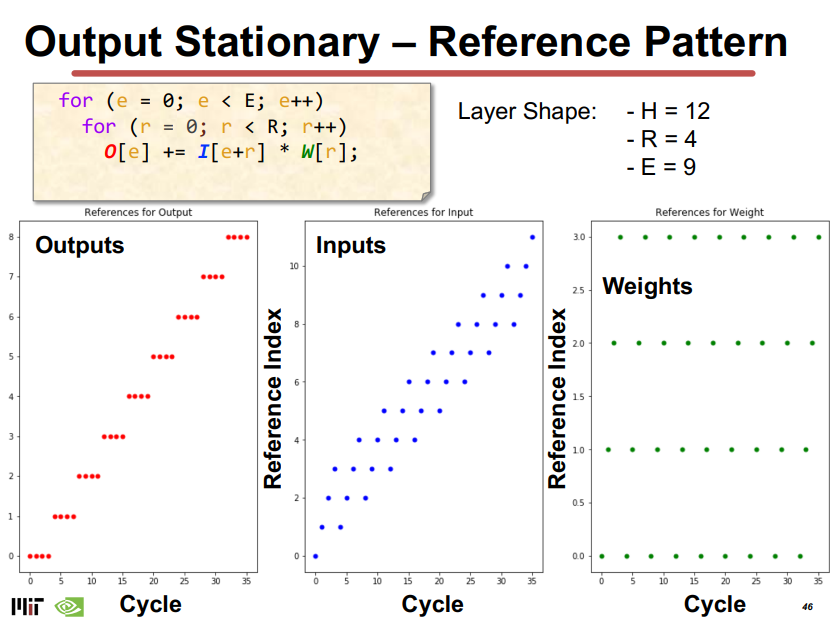
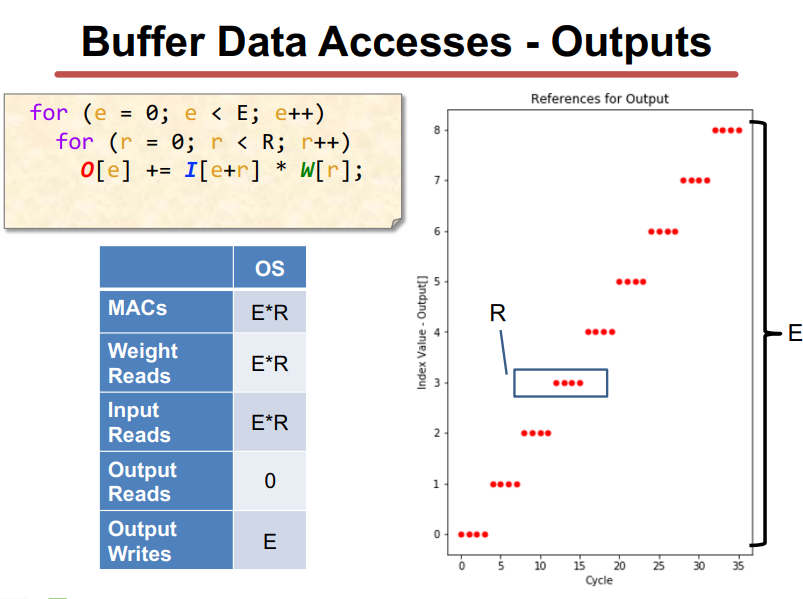
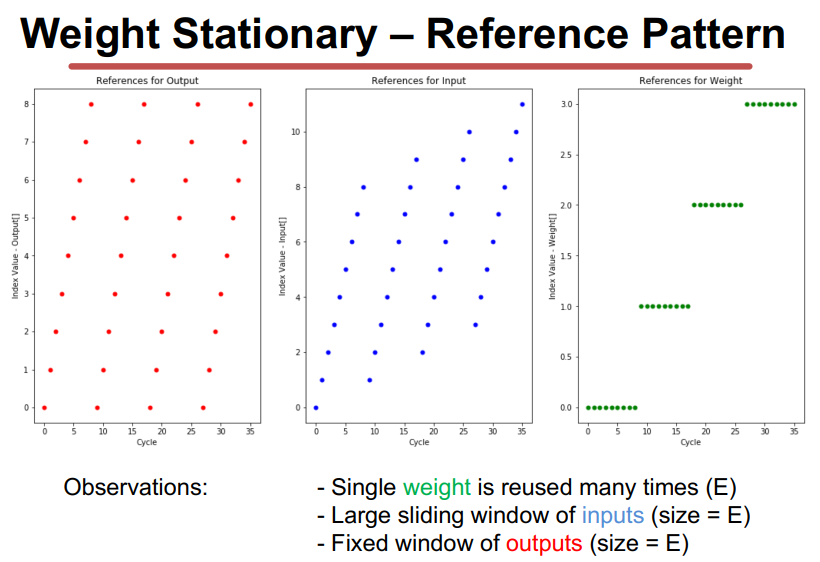
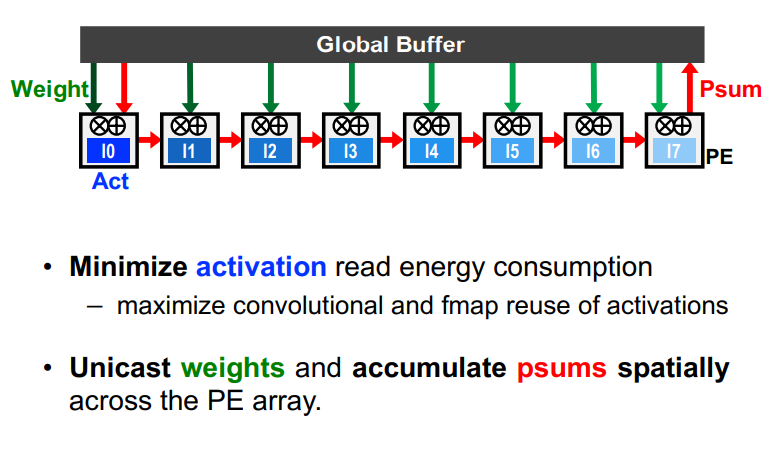
WS
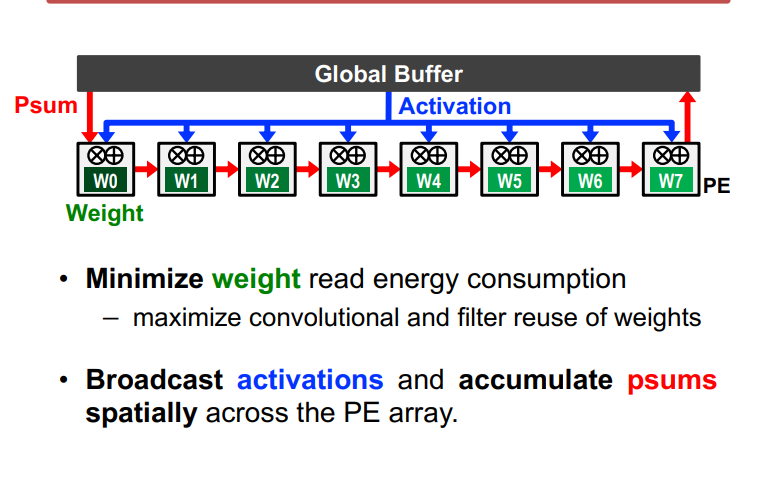
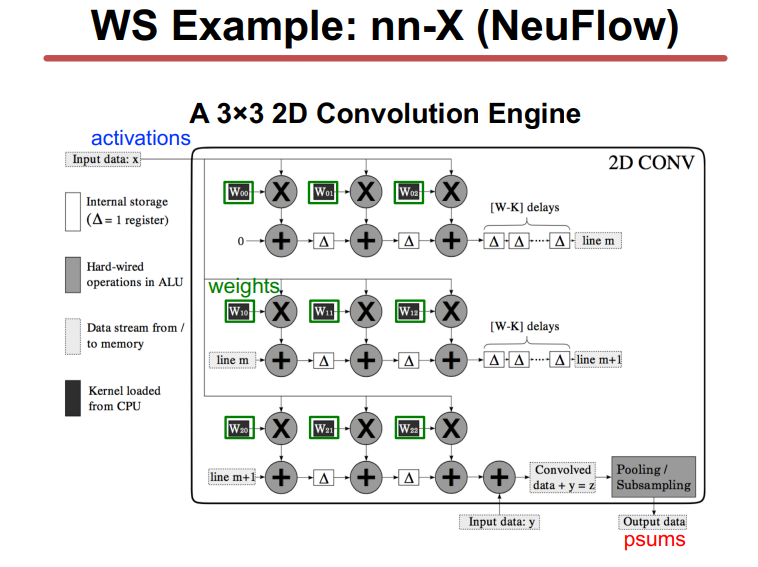
IS
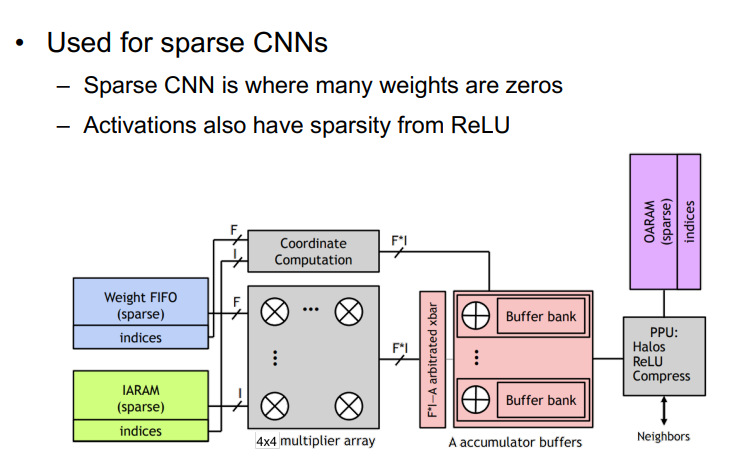
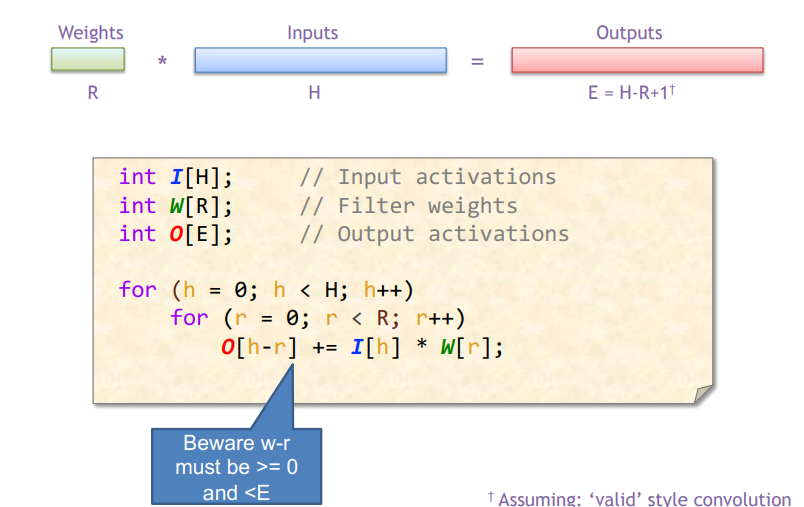
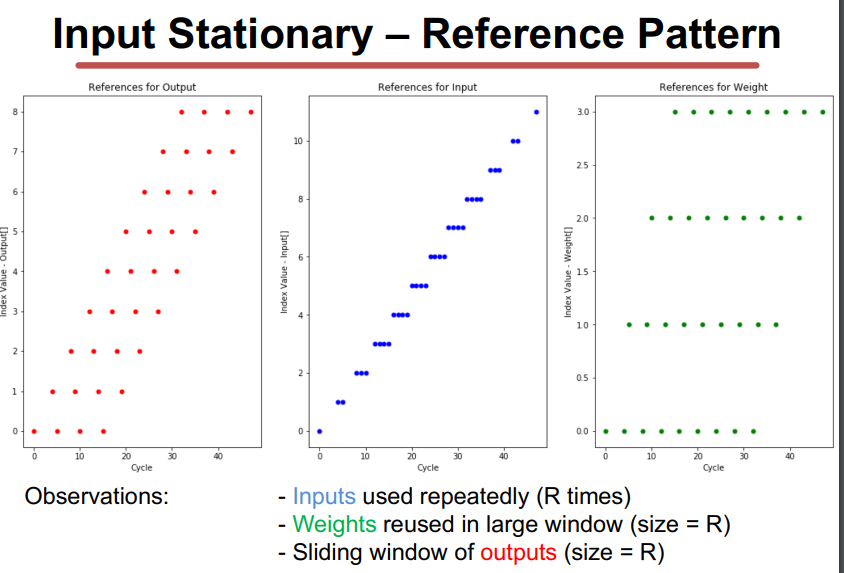
其他方法
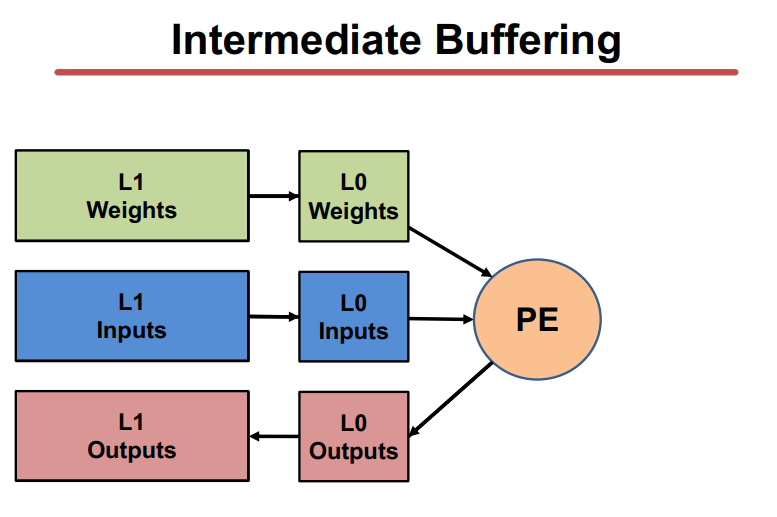
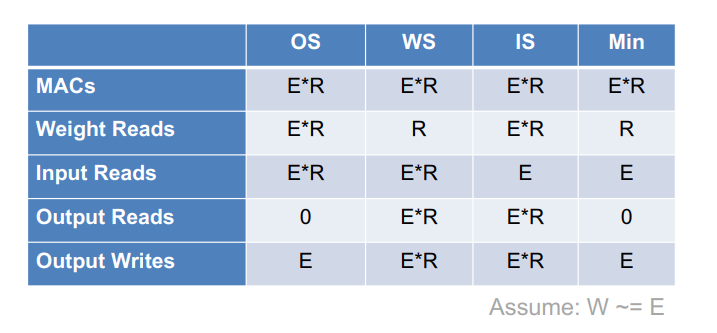
Summary



参考链接
https://www.cnblogs.com/shine-lee/p/10906535.html
https://eyeriss.mit.edu/tutorial.html



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!
2023-05-16 疑难杂记:大话中频带宽和有效带宽